Ответьте на следующие вопросы:
1. Что такое треугольник?
2. Какой треугольник называется прямоугольным?
3. Чему равна сумма двух острых углов прямоугольного треугольника?
4. Как называются стороны прямоугольного треугольника?
5. Как называется большая сторона прямоугольного треугольника?
6. Как найти площадь прямоугольного треугольника, если известны длины его катетов?

Сформулируйте теорему Пифагора.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Задача 1
Катеты прямоугольного треугольника равны 9 и 40. Найдите гипотенузу.
Задача 2
Гипотенуза прямоугольного треугольника равна 29. Один из его катетов равен 21. Найдите другой катет.
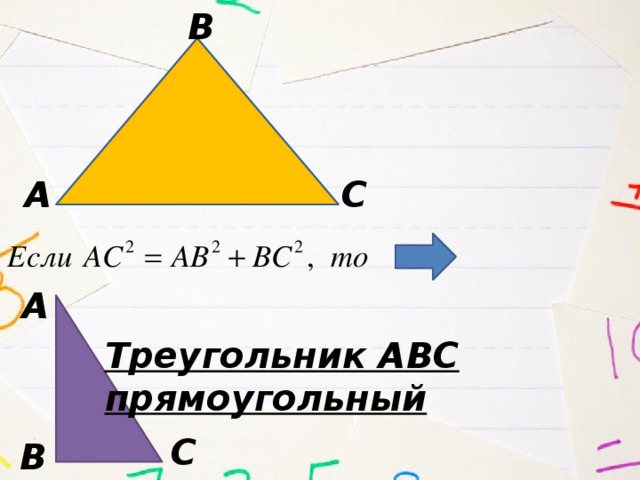
Теорема обратная теореме Пифагора
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный

 Получите свидетельство
Получите свидетельство Вход
Вход





















 Теорема Пифагора и обратная ей (0.17 MB)
Теорема Пифагора и обратная ей (0.17 MB)
 0
0 1888
1888 244
244 Нравится
0
Нравится
0



