Данная работа представляет собой методическую разработку первого урока по теме «Сравнение десятичных дробей». Урок направлен на решение следующих задач: проверка знаний учащихся фактического материала, умений применять знания при решении примеров и задач, совершенствование вычислительных навыков; развитие навыков самостоятельности, самоконтроля, самооценки.
Каждый ученик в ходе урока выполняет определенные задания, самостоятельно оценивает себя за каждое задание и выставляет отметку в индивидуальный оценочный лист. В конце занятия по сумме набранных баллов каждый учащийся выводит итоговую отметку. На этом уроке формируются УУД учащихся: коммуникативные, регулятивные, познавательные, личностные.
| ФИО | Таранова Надежда Александровна |
| Место работы | МОУ ООШ с.Брянкустичи Унечского района Брянской области |
| Должность | Учитель математики |
| Предмет | Математика |
| Класс | 5 |
| Базовый учебник | Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 5: Учебник для учащихся общеобразовательных учреждений, 31 издание, стереотипное. – М. Мнемозина, 2013 |
| Название урока | Сравнение десятичных дробей |
| Тип урока | Урок формирования новых знаний и умений. |
| Форма проведения урока | Традиционная |
| Образовательная среда урока | Компьютер, проектор, учебники по математике, раздаточный материал, индивидуальные карты оценки учеников, мел, доска, электронная презентация, выполненная в программе Power Point. |
| Формы работы учащихся | Фронтальная, индивидуальная, парная. |
| Цель урока | Для учителя | Для ученика | Метапредметные результаты |
|
| Познакомить учащихся с равными и неравными десятичными дробями, учить находить равные дроби, научить учащихся сравнивать десятичные дроби. | Вывести правило сравнения десятичных дробей. Уметь применять полученный алгоритм на практике. | Регулятивные – развивать умение видеть математическую задачу в контексте проблемной ситуации в окружающей жизни; совершенствовать критерии оценки и использовать их в ходе оценки и самооценки. Познавательные – понимать сущность составления алгоритма, действовать по алгоритму, проговаривать выводы в виде правил «если …, то …». Коммуникативные – уметь оформлять свои мысли в устной и письменной речи с учётом речевых ситуаций; уметь слушать собеседника и вести диалог, работать в паре. Личностные - адекватно оценивать результаты своей учебной деятельности, осозновать и принимать социальную роль ученика, объяснять свои достижения, понимать причины успеха в учебной деятельности. |
| Задачи урока: Обучающая – сформулировать правило сравнения десятичных дробей; сформировать умение пользоваться этим правилом. Развивающая – развивать логическое мышление, память, познавательный интерес, продолжить формировать математическую речь, вырабатывать умение анализировать и сравнивать, развивать навыки самоконтроля. Воспитывающая – развитие любознательности и интереса к предмету, воспитание у учащихся навыков учебного труда, формирование ответственности за конечный результат, доброжелательного отношения друг к другу.
|
| Этапы урока
| Деятельность учителя
| Деятельность ученика
| Формируемые УУД
|
|
Организационный ( 1 мин) |
Приветствие учащихся. Проверка учителем готовности класса к уроку; организация внимания.
- Здравствуйте, ребята! Я рада вас всех видеть! Кто сегодня дежурный? Проверьте, пожалуйста, все ли готовы к уроку?
|
Слушают учителя, настраиваются на работу, проверяют готовность к уроку.
|
Умение слушать и вступать в диалог. Умение выделять нравственный аспект поведения.
|
|
Актуализация знаний, проверка домашнего задания ( мин) |
Вступительное слово учителя. Проверка домашнего задания. Самостоятельная работа.
- Откройте тетради, запишите число, классная работа. В своем оценочном листе, который есть у каждого из вас, нарисуйте, пожалуйста, смайлик, который соответствует вашему настроению, с которым вы пришли на урок. Давайте проверим домашнее задание. Дома вы должны были выполнить номера 1167 и 1134(1). Сейчас поменяйтесь тетрадями с соседом и проверьте правильность выполнения домашнего задания. Домашнее задание проверяется устно, комментируется каждый пример, результат отображается на слайдах. - Молодцы, оцените, пожалуйста, работу соседа по пятибалльной шкале и поставьте баллы в индивидуальный оценочный лист.
А теперь вспомним материал предыдущих уроков. Запишите – самостоятельная работа. 1. Записать в виде десятичной дроби числа: 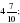 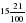 ; ; 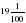 ; ; 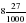 ; ; 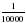
2.Запишите десятичные дроби со знаменателем, т.е. в виде обыкновенной дроби: 3.17; 5,257; 18,02; 1,001; 21,0005 3.Равны ли дроби? а) 0,24=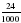 б) 3,76=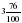 в) 6,001=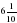
Проверим, что у вас получилось. Проверяем вместе, с помощью слайдов, комментируя и объясняя трудные моменты.
В своем индивидуальном оценочном листе в графе «Самостоятельная работа» поставьте заработанные баллы (за 12- 13 верно решенных «5», за 10-11 – «4», за 7-9 – «3», за 6 и меньше – «2»). Молодцы, справились! |
Проверяют домашнее задание у соседа по парте, оценивают работу, выставляют отметку в оценочный лист.
Выполняют задания математического диктанта, оценивают сами свой результат, выставляют отметку в оценочный лист.
3. Равны ли числа: а) 4,30 и 4,3; б) 0,6 и 0,06; в) 7,2000 и 7,2; г) 19 и 19,00; д) 50,6 и 5,06?
|
Познавательные: применение предметных знаний; выполнение учебных заданий. Регулятивные: Выделение и осознание того, что уже пройдено; Умение распознавать на слух вопросы и отвечать на них. Коммуникативные: Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог. Личностные: Самоооценка, взаимооценка. |
|
Постановка цели и задач урока. Мотивация учащихся. ( мин) |
А теперь мы с вами поработаем в парах. Вы получите задание, будет две-три минутки на обсуждение, а потом мы проверим результаты. Итак, Наташа и Валера – это первая пара, Игорь и Настя - это вторая пара, Настя и Катя - это третья пара. Рассудите спор. Однажды Незнайка пришёл в цирк, и у них с Клоуном возник спор: на таблице написаны числа 8,642 и 0,8642 56,28 и 56,28000
Клоун говорит, что первые два числа равны, так как у них в записи одинаковые цифры, а нуль ничего не значит. А Незнайка утверждает, что второе больше, так как в нём больше знаков. Так же они спорили о вторых числах. Как вы думаете, ребята, кто прав? Поможем им разобраться! Выслушиваем мнения пар, приходим к выводу, что сравнивать десятичные дроби мы еще не умеем. Ставим перед собой цель научиться сравнивать десятичные дроби и формулируем тему урока: «Сравнение десятичных дробей».
|
Работают в парах, обсуждая задание. Комментируют полученный результат. Выявляют проблему, ставят цель и формулируют тему урока.
|
Познавательные: Извлечение из текстов математической информации; Постановка и формулирование проблемы; Самостоятельное формулирование познавательной цели. Регулятивные: Умение анализировать, Целеполагание. Прогнозирование. Коммуникативные: Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог, участвовать в коллективном обсуждении проблем. Работать в паре. Личностные: Самооценка. |
|
Усвоение новых знаний. ( мин)
|
Запишите тему нашего урока: «Сравнение десятичных дробей» Давайте вместе попробуем разобраться, как же сравниваются десятичные дроби, ведь нам нужно разрешить спор, а сейчас решим задачу: Задача 1. Мама к празднику купила 4,5 кг конфет и 2,8 кг печенья. Чего мама купила больше: конфет или печенья? Какие есть мысли по поводу сравнения этой пары чисел? Как вы узнали? Верно, количество целых у первой дроби больше, чем у второй, значит, 4,6 2,8. Какой вывод можно сделать? Молодцы, сначала смотрим на количество целых. Больше будет та дробь, у которой больше целых.
Задача 2. У двух учащихся в классе измерили рост, получились следующие результаты: Учащийся А – 1,5 м; Учащийся Б – 1,3 м; Чей рост больше? Как сравнить эти дроби? Правильно, целых одинаковое количество, но десятых у второй дроби меньше, чем у первой, значит, 1,3 Верно, если целых одинаковое количество, смотрим на десятые, больше будет та дробь, у которой десятых больше. Рассмотрим ещё пару дробей: 5,71 и 5,79. Как вы думаете, как сравнить? Молодцы, если целых и десятых одинаковое количество, значит, смотрим на сотые, больше будет та дробь, у которой сотых больше. Значит, 5,71 На самом деле, уже стало понятно, что, если сотых одинаковое количество, то смотрим на тысячные и т.д.
А как сравнить 2,11 и 2,4? Совершенно верно некоторые из вас заметили, что у числа 2,4 количество десятых больше, чем у числа 2,11, значит, 2,4 2,11. Давайте попробуем убедиться в этом, чтобы не было сомнений. Теперь попробуем сравнить 2,5 и 2,500. Верно, эти дроби равны. Убедимся в этом. 2,5 м=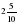 м =2 м 5 дм м =2 м 5 дм 2,50 м=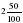 м =2 м 50 см = 2 м 5 дм м =2 м 50 см = 2 м 5 дм 2,500 м=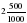 м = 2 м 500 мм = 2 м 5 дм. м = 2 м 500 мм = 2 м 5 дм. Если правые части равны, то равны и левые. Значит, 2,5=2,50=2,500 Итак, мы с вами разобрали все возможные случаи сравнения десятичных дробей. Давайте еще раз сформулируем правило: 1. Для того, чтобы сравнить две десятичные дроби, нужно сначала сравнить количество целых, больше будет та дробь, у которой целых больше, если целых у них одинаково, то сравниваем количество десятых и так далее. 2. Если в десятичной дроби в дробной части в конце записи имеются нули, их можно отбросить и наоборот, любое натуральное число можно записать десятичной дробью, в которой в дробной части будут нули: 6 = 6,00
|
Записывают тему урока. Выполняют вместе с учителем задачи на сравнение дробей. Отвечают на вопросы учителя. Выдвигают предположения. Формулируют правило.
|
Познавательные: Структурирование знаний, Выбор способов решения задач, Анализ объектов и синтез. Регулятивные: Умение оценивать правильность выполнения действия; Планирование пути достижения цели; прогнозирование. Коммуникативные: развитие умения слушать и вступать в диалог, задавать вопросы. Личностные: Осознание ответственности за общее дело |
|
Выполнение учащимися заданий на закрепление пройденного правила. ( мин) |
А теперь попробуем применить наши новые знания на практике. Вернёмся к спору и разрешим его: кто был прав? Молодцы, теперь мы уверенно и правильно ответили на эти вопросы.
Потренируемся еще. № 1175(1,2,3,4,5,6). К доске по очереди выходят те, кого я называю, решают с объяснением по одному примеру. Проверим, научились ли вы сравнивать десятичные дроби. Следующее задание решать будем по вариантам, к доске от каждого варианта будут вызваны ученики. (учащиеся у доски решают примеры на боковых досках, класс не видит их решения). I вариант. II вариант. Сравнить дроби: 12,567 и 125,67; 4,199 и 4,2; 7,399 и 7,4; 1 и 0,59; 0,1 и 0,09; 21, 83 и 20,83; 1,6 и 1,600; 7,02 и 7,0200; 43,5 и 43,12; 18,342 и 183,42; 0,0091 и 0,01. 0,02 и 0,0045. Проверим результат. Если все решено верно, ставим себе 5 баллов в лист оценивания за самостоятельную работу, если верно решено 5 примеров, ставим себе 4 балла, за 3 верно решенных примера ставим себе 3 балла.
|
Отвечают на вопросы учителя. Выполняют письменное задание в тетради и у доски.
Решают примеры по вариантам самостоятельно в тетради, от каждого варианта к доске выходит по одному человеку, решают те же примеры на боковых досках, потом вместе с классом проверяют. Учащиеся проверяют свой результат, выставляют отметку в оценочный лист. |
Познавательные: Уметь решать примеры по выбранному правилу; Применение предметных знаний, выбор способов решения задач. Регулятивные: Умение проговаривать последовательность действий на уроке, анализировать и оценивать результат работы; Коммуникативные: Умение слушать, обращаться с вопросом к учителю и сверстнику Личностные: Самооценка. |
| Применение темы в жизни | Сравнение дробей и чисел - очень важная операция. В медицине, например. Известно, что «великан среди микробов» имеет размер 0,1 мм, а наибольший мелкий вирус имеет размер 16 миллимикрон, т.е. 0,0000016 мм. Сравнивая размеры, медики определяют, чем вызвано заболевание, микробом или вирусом и узнают, какая это болезнь. | Слушают учителя | Познавательные: Применение предметных знаний в жизни. Регулятивные: Умение анализировать и оценивать результат работы; Коммуникативные: Умение слушать Личностные: Смысловая ориентация.
|
|
Подведение итогов урока. Постановка домашнего задания. ( мин) |
Подходит к завершению наш урок, пора подвести итоги. Запишите домашнее задание: № 1200, № 1202, № 1203, правило выучить. Подсчитайте общее количество баллов на вашем оценочном листе и впишите его в последнее пустое окошко. Если вы набрали 14 - 15 баллов, то за урок вы получаете отметку «5»; 11 - 13 – получаете «4»; 8 – 10 – получаете «3». Учащиеся, которые набрали менее 8 баллов, работали сегодня плохо, в следующий раз старайтесь лучше. |
Отвечают на вопросы учителя. Записывают домашнее задание. Подсчитывают общее количество баллов за урок и выставляют себе итоговую отметку.
|
Познавательные: Выделение и формулирование познавательной цели, рефлексия способов и условий действия. Анализ и синтез объектов. Регулятивные: Оценка-осознание уровня и качества усвоения. Коммуникативные: Умение с достаточной полнотой и точностью выражать свои мысли. Личностные: Самооценка, Ценностно-смысловая ориентация |
| Рефлексия. (1 мин) | О чем мы сегодня говорили? Какую цель мы поставили сегодня? Достигли ли мы этой цели? Все ли было понятно, все ли успели? Пригодятся ли вам полученные знания в жизни? Где? Приведите примеры. Я попрошу вас на оценочном листе нарисовать смайлик, соответствующий вашему настроению, с которым вы уходите с урока. Сдайте мне, пожалуйста, Ваши оценочные листы и тетради. Урок окончен! Вы все молодцы! Спасибо за работу!
| Рефлексия. | Познавательные: Рефлексия Регулятивные: Оценка своей деятельности и деятельности других людей Коммуникативные: Умение с достаточной полнотой и точностью выражать свои мысли Личностные: Самооценка на основе критерия успешности. |

 Получите свидетельство
Получите свидетельство Вход
Вход



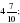
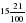 ;
; 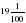 ;
; 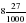 ;
; 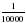
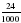
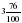
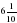
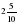 м =2 м 5 дм
м =2 м 5 дм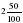 м =2 м 50 см = 2 м 5 дм
м =2 м 50 см = 2 м 5 дм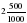 м = 2 м 500 мм = 2 м 5 дм.
м = 2 м 500 мм = 2 м 5 дм.








 Технологическая карта урока по математике «Сравнение десятичных дробей» (42.55 КB)
Технологическая карта урока по математике «Сравнение десятичных дробей» (42.55 КB)
 0
0 924
924 218
218 Нравится
0
Нравится
0


