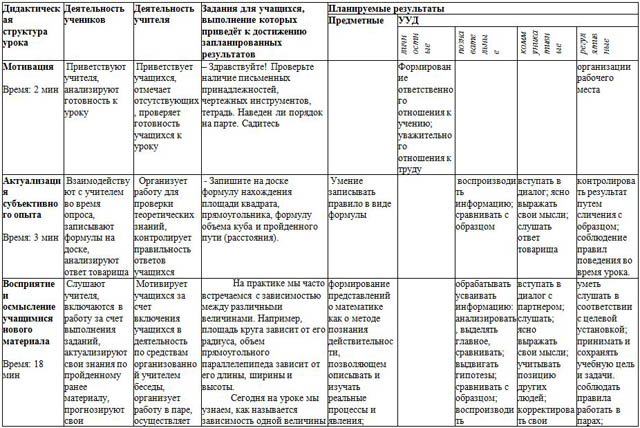
Цель урока:
- организовать деятельность учащихся по восприятию, осмыслению и первичному закреплению новых знаний и способов деятельности.
- формирование у учащихся математического понятия «функция».
Задачи:
Образовательные:
– познакомить учащихся с понятиями функция, аргумент, область определения функции; познакомить учащихся со способами задания функции.
Развивающие:
– формировать в процессе обучения познавательную активность; умение приобретать и творчески распоряжаться полученными знаниями.
Воспитательные:
– обеспечить устойчивую мотивационную среду, интерес к изучаемой теме; воспитывать самоорганизацию работы на уроке; формировать видение целостности картины мира.
Ход урока.
1. Мотивация.
Приветствует учащихся, отмечает отсутствующих, проверяет готовность учащихся к уроку.
– Здравствуйте! Проверьте наличие письменных принадлежностей, чертежных инструментов, тетрадь. Наведен ли порядок на парте. Садитесь.
2. Актуализация субъективного опыта.
Организует работу для проверки теоретических знаний, контролирует правильность ответов учащихся.
- Запишите на доске формулу нахождения площади квадрата, прямоугольника, формулу объема куба и пройденного пути (расстояния).
3. Восприятие и осмысление учащимися нового материала.
Мотивирует учащихся за счет включения учащихся в деятельность по средствам организованной учителем беседы, организует работу в паре, осуществляет выборочный контроль, слушает и отмечает правильность ответа учащихся.
Организует выполнения задач, констатирует тему урока, контролирует записи в тетради.
На практике мы часто встречаемся с зависимостью между различными величинами. Например, площадь круга зависит от его радиуса, объем прямоугольного параллелепипеда зависит от его длины, ширины и высоты.
Сегодня на уроке мы узнаем, как называется зависимость одной величины от другой.
Карточка.
Задание. Рассмотрите задачу в паре и ответьте на вопросы.
Площадь квадрата зависит от длины его стороны. Пусть сторона квадрата равна, а см, а его площадь равна S см².
1. Запишите зависимость площади квадрата от длины его стороны.
2. Найдите площадь квадрата, если длина сторона квадрата равна 3, 14, 0,3, 0,08.
3. Какая переменная будет является зависимой, а какая независимой?
Ответ: Зависимость переменной S от переменной a выражается формулой S=a2.
Если а = 3, то S=3²=9;
Если а = 14, то S=14²=196;
Если а = 0,3, то S=0,3²=0,09;
Если а = 0,08, то S=0,08²=0,0064.
Переменную а, значение которой выбирают произвольно, называют независимой переменной, а переменную S, значение которой определяются выбранными значениями а, называют зависимой переменной.
- Давайте рассмотрим еще примеры. Определим, какая переменная является зависимой, а какая не зависимой.
Пример. Путь, пройденный автомобилем со скоростью 50 км/ч, зависит от времени движения.
s=50t
Если t=0,5, то s=50·0,5=25;
Если t=1, то s=50·1=50;
Если t=2, то s=50·2=100;
Если t=3,5, то s=50·3,5=175.
t – независимая переменная, s – зависимая переменная
Пример. Зависимость температуры воздуха от времени суток.
Если t=0, то p= – 4;
Если t=12, то p= 2;
Если t=17, то p= 3;
Если t=22, то p= 0.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



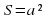 .
. , значение которой определяются выбранными значениями а, называют зависимой переменной.
, значение которой определяются выбранными значениями а, называют зависимой переменной.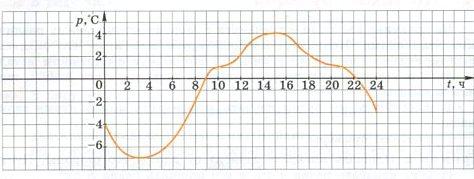
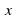 см равна
см равна 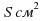 . Выразите формулой зависимость
. Выразите формулой зависимость 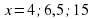 найдите соответствующее значение функции
найдите соответствующее значение функции 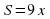
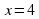 , то
, то 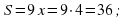
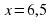 , то
, то 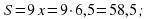
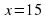 , то
, то 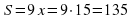 .
. ;
;  ;
; 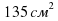 .
.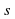 км. Задайте формулой зависимость
км. Задайте формулой зависимость 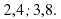
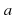 см – длина ребра куба, а
см – длина ребра куба, а 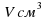 – его объем. Задайте формулой зависимость
– его объем. Задайте формулой зависимость 








 Технологическая карта урока по алгебре "Что такое функция?" (63.95 КB)
Технологическая карта урока по алгебре "Что такое функция?" (63.95 КB)
 0
0 3126
3126 512
512 Нравится
0
Нравится
0


