THE FORMATION OF THE COMPUTING CULTURE OF JUNIOR SCHOOLCHILDREN IN LEARNING MATHEMATICS
ФОРМИРОВАНИЕ ВЫЧИСЛИТЕЛЬНОЙ КУЛЬТУРЫ МЛАДШИХ ШКОЛЬНИКОВ В ПРОЦЕССЕ ОБУЧЕНИЯ МАТЕМАТИКЕ
Картошкина Ирина Михайловна
студентка 4 курса психолого-педагогического факультета, Чувашский
государственный педагогический университет им. И. Я. Яковлева,
г. Чебоксары
Kartoshkina Irina Mikhailovna
Student, the Chuvash I. Yakovlev State Pedagogical University
Cheboksary
Аннотация: в данной статье раскрывается важность формирования вычислительной культуры младших школьников. Дана характеристика понятиям «вычислительный навык» и «вычислительная культура». Перечислены качества, характеризующие полноценный вычислительный навык. Рассмотрены способы формирования вычислительной культуры.
Abstract: the article reveals the necessity of formation computing culture of primary school students. The characteristic of concepts "computer skill" and "computer culture." Lists the qualities that characterize a full-fledged computing skill. The methods of forming a computing culture.
Ключевые слова: вычислительный навык, вычислительная культура, компетенция.
Keywords: computer skill, computer culture, student competence.
Формирование вычислительной культуры является одной из фундаментальных задач начального курса математики. Оно тесно связано с качеством вычислений и развитием вычислительной компетентности. Есть предположение, что калькуляторы оказывают пагубное воздействие на качество вычислений младших школьников, так как при их использовании ученики не видят потребности в развитии своих вычислительных способностей. С этим мнением можно согласиться не всегда, только в части выполнения письменных вычислений. Невозможно использовать калькулятор без понимания того, как читают, записывают и сравнивают числа, какие есть знаки действий и каковы условия их применения, в чем суть основ вычислительных операций. Для формирования умения выполнять вычисления на калькуляторе необходимо владеть предполагаемым результатом, его проверкой и оценкой, которые могут быть сформированы только в вычислениях без применения вычислительной техники.
Вычислительную компетентность младшего школьника можно охарактеризовать как черту личности, которая проявляется в индивидуальной готовности и умении выполнять вычислительные операции в различных ситуациях. Формировать вычислительную компетентность необходимо начинать с I класса, так как именно этот период является благоприятным для формирования черт личности. В этот период ученик впитывает в себя знания, которые в дальнейшем становятся умениями, а затем — чертой личности, т.е. перерастают в компетентность. Если этот период упустить, то сформировать вычислительную компетентность личности не удастся никогда.
Также для развития вычислительной культуры младших школьников нужно вводить в этапы урока её неотъемлемую часть – устный счет.
В качестве задания можно предложить упражнение «Заполни таблицу».
| 15 | ? | 17 | 29 |
| 10 | 10 | ? | 18 |
| ? | 40 | 25 | ? |
| 57 | ? | 48 | 29 |
| 10 | 10 | ? | 18 |
| ? | 45 | 25 | ? |
Он может проводиться как в начале урока, так и на любом его этапе. Упражнения в устных вычислениях должны пронизывать весь урок. Их можно соединять с проверкой домашних заданий, закреплением изученного материала, предлагать при опросе. Особенно хорошо, если наряду с этим, специально отводить 5–7 минут на уроке для устного счёта. Материал для этого можно подобрать как из учебника, так и из специальных сборников. Хорошо пользуется популярностью использовать «числовые дорожки» в качестве минутки чистописания, например, при изучении темы «Сложение и вычитание чисел в пределах 10»:
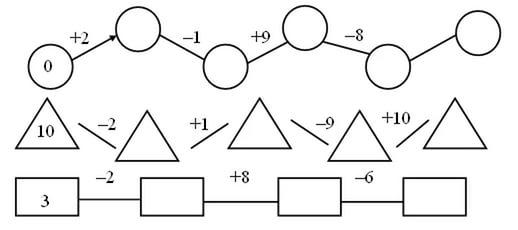
Устные упражнения должны соответствовать теме и цели урока и помогать усвоению изучаемого на данном уроке или ранее пройденного материала.
Так как времени, отводимого на объяснение материала на уроке недостаточно для полноценного развития вычислительной культуры, необходимо проводить внеклассные мероприятия в форме занимательных уроков, викторин. Например, можно познакомить детей со способами быстрого умножения. Рассмотрим некоторые из них:
1) умножение двузначного числа на 11 (Чтобы умножить на 11 двузначные числа, сумма цифр которого ≥10, надо между цифрой десятков, увеличенной на 1, и цифрой единиц написать избыток суммы цифр числа над десятью): 68*11=748, 69*11=759.
2) умножение на 5,25,125 (Чтобы умножить число на 5,25,125, достаточно разделить его соответственно на 2,4,8 и результат умножить на 10,100,1000.): 64*125=8000,64*25=1600.
3) умножение на 9,99,999 (Чтобы умножить число, написанное девятками, надо к множимому приписать справа столько нулей, сколько девяток в множителе и из результата вычесть множимое):387*9=3870-387=3483,24*99=2400-24=2376.
4) умножение по способу Гаусса (Любое умножение целых чисел можно привести к умножению одного из них на 5,2 и 1 или на круглые числа, записанные только этими цифрами, путем замены другого сомножителя суммой или разностью соответствующим образом подобранных чисел):89*27=? Представим число 27 в виде суммы трех чисел(20+5+2) и, подставив, получим: 89*27=89*(20+5+2)=1780+445+178=2403.
Приобрести вычислительные навыки – значит, для каждого случая знать, какие операции и в каком порядке следует выполнить, чтобы найти значение математического выражения, и производить эти операции в достаточно быстром темпе.
Структура любой компетентности включает в себя четыре составляющих: знания, ценностное отношение к знаниям, готовность к применению знаний и опыт в применении полученных знаний.
Ценностное отношение к знаниям и готовность к их применению тесно связаны между собой. Между ними лишь тонкая грань, которую опытному педагогу необходимо четко различать. Переходить к третьему этапу надо тогда, когда школьник почувствует необходимость в получении новых знаний. Например, в I классе изучение темы «Числа от 11 до 20» можно начать следующим диалогом.
Учитель (У.). Сколько будет 9 + 3?
Дети (Д.). 9. У. Сколько будет 3 + 9?
Д. Мы не знаем, потому что результат больше 10, а такие примеры мы еще не встречали.
У. Что мы должны знать, чтобы решить этот пример?
Д. Как прибавлять числа с переходом через десяток.
У. Необходимо ли нам это знание?
Д. Да.
У. Где нам могут пригодиться эти знания?
Д. При счете денег в магазине, при дальнейшем вычислении.
Теперь можно переходить к следующему этапу, ведь первоклассники готовы к получению и применению знаний.
Таким образом, использование устного счета для формирования вычислительной культуры способствует развитию памяти, внимания, быстроте реакции, воспитанию умения сосредоточиться, наблюдать, проявляется инициатива учащихся, потребность к самоконтролю. Отточенный навык устного счета косвенным образом способствует развитию вычислительной культуры, быстрейшей обучаемости детей начальной школы, воспитывает в них внимание и интерес к предмету при правильной подаче материала на уроке.
Список литературы
Ефимов, В. Ф. Формирование вычислительной культуры младших школьников / В. Ф. Ефимов // Начальная школа. – 2014. – № 1. – С. 61—66.
Зайцева, С. А. Методика обучения математике в начальной школе / С. А. Зайцева, И. Б. Румянцева, И. И. Целищева. – Москва: Гуманитар. изд. центр Владос, 2008.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Статья на тему "ФОРМИРОВАНИЕ ВЫЧИСЛИТЕЛЬНОЙ КУЛЬТУРЫ МЛАДШИХ ШКОЛЬНИКОВ В ПРОЦЕССЕ ОБУЧЕНИЯ МАТЕМАТИКЕ" (42.95 KB)
Статья на тему "ФОРМИРОВАНИЕ ВЫЧИСЛИТЕЛЬНОЙ КУЛЬТУРЫ МЛАДШИХ ШКОЛЬНИКОВ В ПРОЦЕССЕ ОБУЧЕНИЯ МАТЕМАТИКЕ" (42.95 KB)
 0
0 348
348 4
4 Нравится
0
Нравится
0


