Получите свидетельство
Вход
Учебник «Информатика и ИКТ». 10 класс /сост. Гейн А. Г., М.: Просвещение, 2017
Глава 4. «Логико-математические модели»
§30 Элементы логики высказываний
Пашкин Игорь Алексеевич учитель информатики, высшей квалификационной категории, ГБОУ школа №100 Калининского района Санкт-Петербурга
1
Автор: © Пашкин Игорь Алексеевич
§30 Элементы логики высказываний
Автор: © Пашкин Игорь Алексеевич
Логические операции
3
Автор: © Пашкин Игорь Алексеевич
Таблица истинности
4
Автор: © Пашкин Игорь Алексеевич
Простые и сложные высказывания
Высказывания бывают простые и сложные.
Высказывание называется простым , если никакая его часть сама не является высказыванием.
Сложные (составные) высказывания строятся из простых с помощью логических операций .
Название логической операции
Конъюнкция
Логическая связка
Дизъюнкция
«и»; «а»; «но»; «хотя»
«или»
Инверсия
«не»; «неверно, что»
5
Автор: © Пашкин Игорь Алексеевич
Логические операции
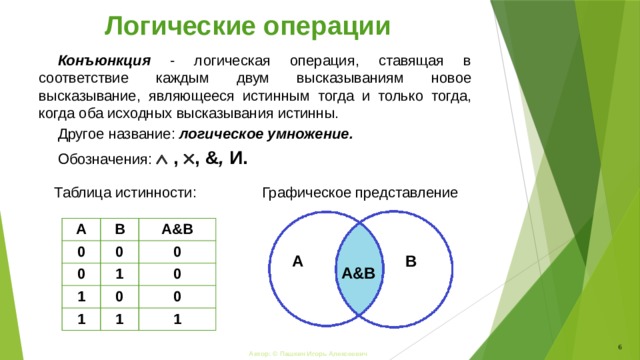
Конъюнкция - логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Другое название: логическое умножение.
Обозначения: , , & , И.
Графическое представление
Таблица истинности:
А
0
В
0
А&В
0
1
0
1
1
0
0
1
0
1
A
B
А&В
6
Автор: © Пашкин Игорь Алексеевич
Логические операции
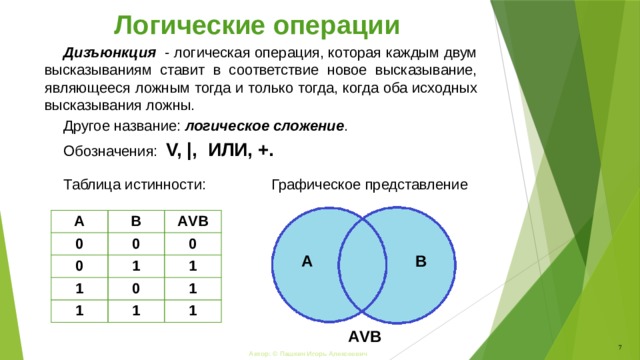
Дизъюнкция - логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
Другое название: логическое сложение .
Обозначения: V, |, ИЛИ, +.
Графическое представление
Таблица истинности:
А
0
В
0
АVВ
0
1
0
1
1
0
1
1
1
1
A
B
АVВ
7
Автор: © Пашкин Игорь Алексеевич
Логические операции
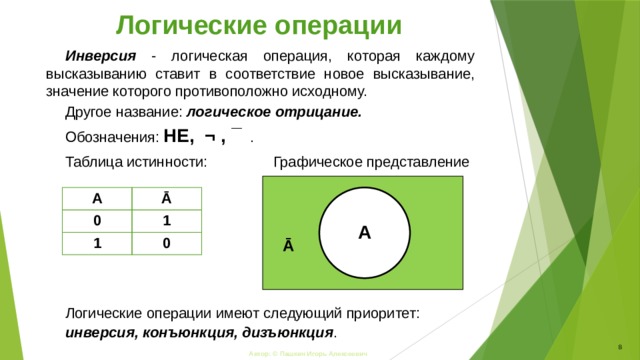
Инверсия - логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.
Другое название: логическое отрицание.
Обозначения: НЕ, ¬ , ¯ .
Таблица истинности:
Графическое представление
А
0
Ā
1
1
0
A
Ā
Логические операции имеют следующий приоритет:
инверсия, конъюнкция, дизъюнкция .
8
Автор: © Пашкин Игорь Алексеевич
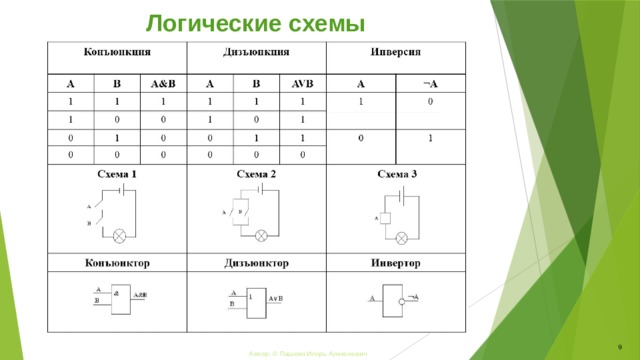
Логические схемы
9
Автор: © Пашкин Игорь Алексеевич
Использование электронного конструктора «ЗНАТОК» на уроках «Информатика и ИКТ»
10
Автор: © Пашкин Игорь Алексеевич
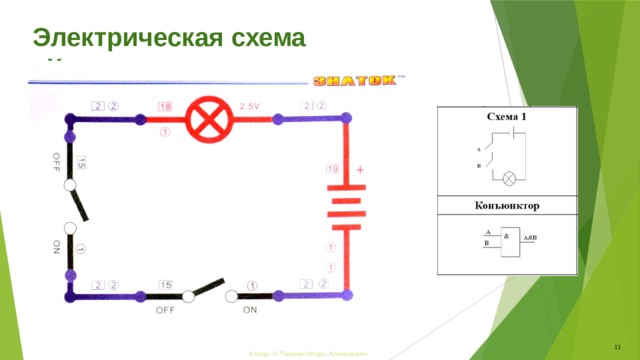
Электрическая схема «Коъюнктора»
11
Автор: © Пашкин Игорь Алексеевич
Лабораторная работа №19 (к §30 §32 и §33) Электрическая схема «Конъюнктора»
1
Автор: © Пашкин Игорь Алексеевич
Электрическая схема «Коъюнктора»
13
Автор: © Пашкин Игорь Алексеевич
Лабораторная работа №19 (к §30 §32 и §33) Электрическая схема «Дизъюнктора»
14
Автор: © Пашкин Игорь Алексеевич
Электрическая схема «Дизъюнктора»
15
Автор: © Пашкин Игорь Алексеевич
Источники информации и WEB-ресурсы
- «Информатика и ИКТ». Учебник для 10 классов / А.Г. Гейн, А.Б. Ливчак, А.И. Сенокосов, Н.А. Юнерман. – 3-е изд., – М.: Просвещение 2017г. «Информатика и ИКТ» 10 класс. Методические рекомендации/А.Г. Гейн. – 2 – е изд., - М.: Просвещение 2017 г. Учебник по базовому курсу Л.Л. Босова. «Информатика» Базовый курс. 8 класс» – Москва, БИНОМ: Лаборатория знаний, 2019 г.
- «Информатика и ИКТ». Учебник для 10 классов / А.Г. Гейн, А.Б. Ливчак, А.И. Сенокосов, Н.А. Юнерман. – 3-е изд., – М.: Просвещение 2017г.
- «Информатика и ИКТ» 10 класс. Методические рекомендации/А.Г. Гейн. – 2 – е изд., - М.: Просвещение 2017 г.
- Учебник по базовому курсу Л.Л. Босова. «Информатика» Базовый курс. 8 класс» – Москва, БИНОМ: Лаборатория знаний, 2019 г.
Электронные учебные пособия
- http://www.metodist.ru Лаборатория информатики МИОО
- http://www.it-n.ru Сеть творческих учителей информатики
- http://www.metod-kopilka.ru Методическая копилка учителя информатики
- http :// fcior . edu . ru http://eor.edu.ru Федеральный центр информационных образовательных ресурсов (ОМC)
- http://pedsovet.su Педагогическое сообщество
- http://school-collection.edu.ru Единая коллекция цифровых образовательных ресурсов
16
Автор: © Пашкин Игорь Алексеевич
§30 Элементы логики высказываний (10 класс, учебник Гейн А.Г.) (22.66 MB)
0
221
12
Нравится
0
