Среднесрочное планирование по геометрии (9 класс)

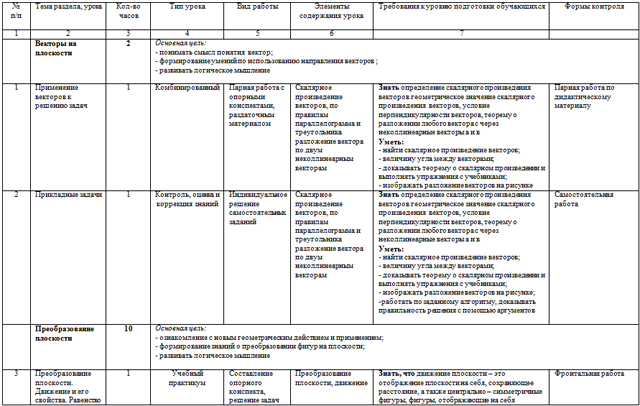
№ п/п

Тема раздела, урока

Кол-во часов

Тип урока

Вид работы

Элементы содержания урока

Требования к уровню подготовки обучающихся

Формы контроля

1

2

3

4

5

6

7

Векторы на плоскости

2

Основная цель:

- понимать смысл понятия вектор;

- формирование умений по использованию направления векторов ;

- развивать логическое мышление

1

Применение векторов к решению задач

1

Комбинированный

Парная работа с опорными

конспектами, раздаточным материалом

Скалярное произведение векторов, по правилам параллелограмма и треугольника разложение вектора по двум неколлинеарным векторам

Знать определение скалярного произведения векторов геометрическое значение скалярного произведения векторов, условие перпендикулярности векторов, теорему о разложении любого вектора с через неколлинеарные векторы а и в

Уметь:

- найти скалярное произведение векторов;

- величину угла между векторами;

- доказывать теорему о скалярном произведении и выполнять упражнения с учебниками;

- изображать разложение векторов на рисунке

Парная работа по дидактическому материалу

2

Прикладные задачи

1

Контроль, оценка и коррекция знаний

Индивидуальное решение самостоятельных заданий

Скалярное произведение векторов, по правилам параллелограмма и треугольника разложение вектора по двум неколлинеарным векторам

Знать определение скалярного произведения векторов геометрическое значение скалярного произведения векторов, условие перпендикулярности векторов, теорему о разложении любого вектора с через неколлинеарные векторы а и в

Уметь:

- найти скалярное произведение векторов;

- величину угла между векторами;

- доказывать теорему о скалярном произведении и выполнять упражнения с учебниками;

- изображать разложение векторов на рисунке;

-работать по заданному алгоритму, доказывать правильность решения с помощью аргументов

Самостоятельная работа

Преобразование плоскости

10

Основная цель:

- ознакомление с новым геометрическим действием и применением;

- формирование знаний о преобразовании фигур на плоскости;

- развивать логическое мышление

3

Преобразование плоскости. Движение и его свойства. Равенство фигур и его свойства

1

Учебный практикум

Составление опорного конспекта, решение задач

Преобразование плоскости, движение

Знать, что движение плоскости – это отображение плоскости на себя, сохраняющее расстояние, а также центрально – симметричные фигуры, фигуры, отображающие на себя

Уметь

- применять их свойства при решении задач

- аргументировано отвечать на поставленные вопросы, осмыслить ошибки и устранить их;

- развернуто обосновывать суждения

Фронтальная работа

4

Осевая и центральная симметрия

1

Комбинированный, поисковый

Работа с конспектом с книгой и наглядными пособиями по парам

Преобразование плоскости, движение, осевая и центральная симметрия

Знать, что движение плоскости – это отображение плоскости на себя, сохраняющее расстояние, а также центрально – симметричные фигуры, фигуры, отображающие на себя

Научить учащихся распознавать два вида симметрии

Уметь

- построить фигуру, симметричную относительно данной точки и относительно прямой на плоскости

- различать два вида симметрии относительно точки и прямой

- применять их свойства при решении задач

- аргументировано отвечать на поставленные вопросы, осмыслить ошибки и устранить их;

- развернуто обосновывать суждения

Парная работа

5

Параллельный перенос, поворот – как движение плоскости

1

Учебный практикум

Составление опорного конспекта, решение задач

Преобразование плоскости, движение, осевая и центральная симметрия, параллельный перенос и поворот

Знать, что движение плоскости – это отображение плоскости на себя, сохраняющее расстояние, а также центрально – симметричные фигуры, фигуры, отображающие на себя

Уметь

- выполнять поворот фигуры;

- применять их свойства при решении задач;

- аргументировано отвечать на поставленные вопросы, осмыслить ошибки и устранить их;

- развернуто обосновывать суждения

Групповая работа

6

Гомотетия

1

Комбинированный

Решение упражнений, составление опорного конспекта

Преобразование плоскости, движение, гомотетия

Знать определение гомотетии

Уметь:

- применять свойства гомотетии при решении задач;

- работать по заданному алгоритму, доказывать правильность решения с помощью аргументов

Парная работа

7

Преобразование подобия и его свойства. Подобные фигуры. Самостоятельная работа № 3

1

Проблемно - поисковый

Работа с опорными конспектами, раздаточным материалом,

в группах

Преобразование плоскости, движение, осевая и центральная симметрия, параллельный перенос и поворот

Знать определение подобных треугольников

Уметь:

- выделять три признака подобия треугольников;

- применять их при решении задач;

- работать по заданному алгоритму, доказывать правильность решения с помощью аргументов

Самостоятельная работа

8

І и ІІ признаки подобия треугольников

1

Поисковый

Работа с опорными конспектами, раздаточным материалом,

в группах

Преобразование плоскости, движение, осевая и центральная симметрия, параллельный перенос и поворот

Знать определение подобных треугольников

Уметь:

- выделять три признака подобия треугольников;

- применять их при решении задач;

- работать по заданному алгоритму, доказывать правильность решения с помощью аргументов

Фронтальная работа

9

ІІІ признак подобия треугольников

1

Комбинированный

Решение упражнений, составление опорного конспекта

Преобразование плоскости, движение, осевая и центральная симметрия, параллельный перенос и поворот

Знать определение подобных треугольников

Уметь:

- выделять три признака подобия треугольников;

- применять их при решении задач;

- работать по заданному алгоритму, доказывать правильность решения с помощью аргументов

Фронтальная работа

10

Задач на применение признаков подобия треугольников

1

Комбинированный

Решение упражнений, составление опорного конспекта

Преобразование плоскости, движение, осевая и центральная симметрия, параллельный перенос и поворот

Знать определение подобных треугольников

Уметь:

- выделять три признака подобия треугольников;

- применять их при решении задач;

- работать по заданному алгоритму, доказывать правильность решения с помощью аргументов

Математический диктант

11

Подобие прямоугольных треугольников

1

Комбинированный, поисковый

Индивидуальное решение контрольных заданий

Преобразование плоскости, движение, осевая и центральная симметрия, параллельный перенос и поворот

Знать определение подобных треугольников

Уметь:

- выделять три признака подобия треугольников;

- применять их при решении задач;

- работать по заданному алгоритму, доказывать правильность решения с помощью аргументов

Самостоятельная работа

12

Контрольная работа № 2

1

Контроль, оценка и коррекция знаний

Проверка знаний, умений, навыков

Преобразование плоскости, движение, осевая и центральная симметрия, параллельный перенос и поворот

Уметь:

- расширять и обобщать сведения о преобразовании плоскости и его свойствах;

- владеть навыками контроля и оценки своей деятельности, предвидеть возможные последствия своих действий.

Контрольная работа

Многоугольники

13

Основная цель:

- ознакомление с новым геометрическим действием и применением;

- формирование определения многоугольники;

- развивать логическое мышление

13

Анализ контрольной работы. Ломаная. Выпуклые многоугольники. Сумма углов выпуклого многоугольника

1

Проблемно -поисковый

Работа с опорными конспектами, раздаточным материалом,

в группах

Многоугольники, выпуклые многоугольники, теорема синусов и косинусов

Знать определение многоугольников, теорему синусов и косинусов;

Уметь:

- применять теоремы при решении задач;

- работать по заданному алгоритму, доказывать правильность решения с помощью аргументов

Групповая работа