ПОВТОРИ И ЗАПОМНИ-5
Десятичные дроби. Сложение и вычитание.
Алгоритм сложения (вычитания) дробей
Чтобы сложить (вычесть) десятичные дроби, надо:
1) Уравнять в дробях число знаков после запятой.
2) Записать их “в столбик” так, чтобы запятая оказалась под запятой.
3) Выполнить сложение (вычитание), не обращая внимания на запятую.
4) Поставить в ответе запятую под запятой в данных дробях.

Умножение десятичных дробей
Алгоритм умножения десятичных дробей
Чтобы перемножить десятичные дроби, надо:
1) Отбросить в множителях запятые и перемножить получившиеся натуральные числа.
2) В полученном произведении отделить запятой справа столько знаков после запятой, сколько их в обоих множителях вместе.
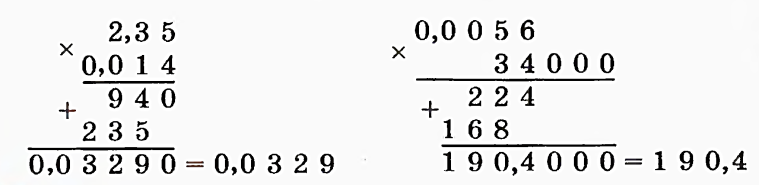
Деление десятичных дробей
Алгоритм деления десятичных дробей
Чтобы поделить десятичную дробь на натуральное число, надо:
1) Выполнить деление целой части.
2) Поставить в частном запятую.
3) Продолжить деление, не обращая внимания на запятую, дописывая в делимом после запятой столько нулей, сколько потребуется.
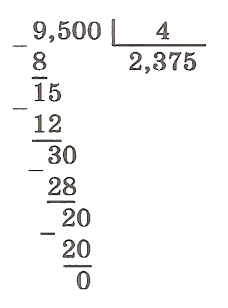
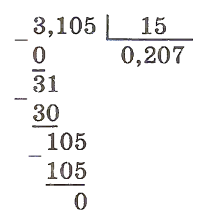
Чтобы поделить десятичную дробь на десятичную дробь, надо:
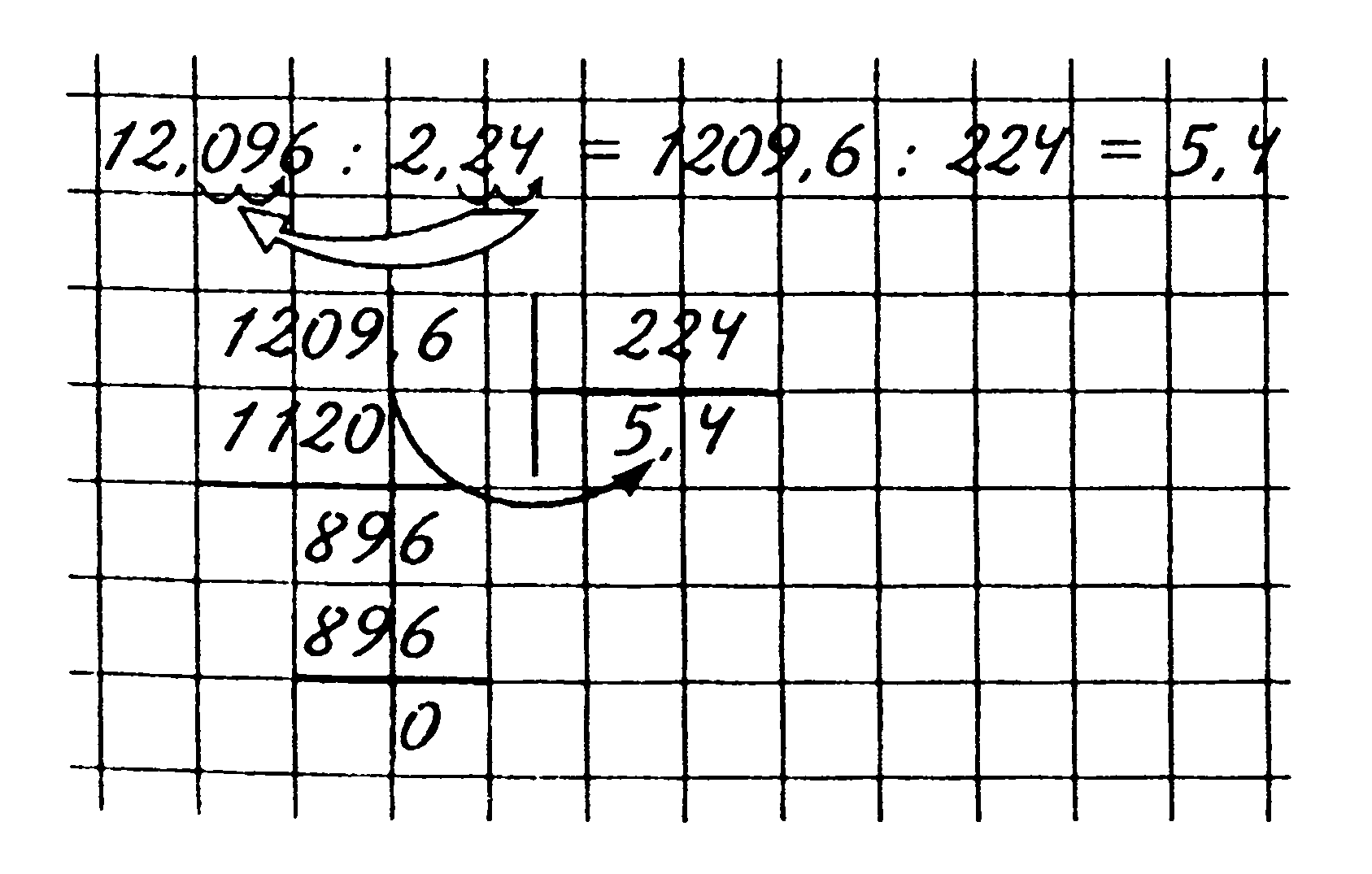
1) Перенести в делимом и в делителе запятую вправо на столько цифр, сколько их после запятой в делителе.
2) Выполнить деление на натуральное число.
Умножение и деление десятичных дробей на 10, 100, 1000 и т.д.
Чтобы умножить или разделить десятичную дробь на 10,100,1000 и т.д., надо перенести запятую соответственно на 1, 2, 3 и т.д. разряда вправо, а при делении - на 1, 2, 3 и т.д. разряда влево.
2,75 10 = 27,5; 2,75 : 10 = 2,75;
2,75 100 = 275; 2,75 : 100 = 0,275;
2,75 1000 = 2750; 2,75 : 1000 = 0,0275;
2,75 10 000 = 275000; 2,75 : 10 000 = 0,000275;
Умножение и деление десятичных дробей на 0,1; 0,01; 0,001 и т.д.
Заметим, что при умножении числа на 0,1; 0,01; 0,001 и т.д. оно уменьшается соответственно в 10, 100, 1000 и т.д. раз, а при делении увеличивается в 10, 100, 1000 и т.д. раз
Поэтому чтобы умножить или разделить десятичную дробь на 0,1; 0,01; 0,001 и т.д., надо перенести запятую соответственно на 1, 2, 3 и т.д. разряда влево, а при делении - на 1, 2, 3 и т.д. разряда вправо.
2,75 0,1 = 0,275; 2,75 : 0,1 = 27,5;
2,75 0,01 = 0,0275; 2,75 : 0,01 = 275;
2,75 0,001 = 0,00275; 2,75 : 0,001 = 27500;
2,75 0,0001 = 0,000275; 2,75 : 0,0001 = 275000;
Применение десятичных дробей
|
|
1 км = 1000 м, 1 ч = 60 мин
1 м = 0,001 км, 1 с = 1/3600 ч |
Чтобы записать число в более мелких единицах, надо умножить его на 10, 100, 1000 и т.д.
5,3м = 530см; 5,3м = 5,3 100см = 530см; 1м = 100см
0,18м = 1,8дм; 0,18м = 0,18 10дм = 1,8дм; 1м = 10дм
12,7 км = 12700м; 12,7км = 12,7 1000м = 12700м; 1км = 1000м
Чтобы записать число в более крупных единицах, надо умножить его на 0,1; 0,01; 0,001 и т.д.
29 кг = 0,029т; 29 кг = 29 0,001 т = 0,029 т; 1 кг = 0,001 т
17,5 ц = 1,75т; 17,5 ц = 17,5 0,1 т = 1,75 т; 1 ц = 0,1 т
8,4 кг = 0,084 ц; 8,4 кг = 8,4 0,01 ц = 0,084 ц; 1 кг = 0,01 ц
250 г = 0,25 кг; 250 г = 250 0,001 кг = 0,25 кг; 1 г = 0,001 кг
Чтобы записать число процентов в виде десятичной дроби, надо данное число разделить на 100
7 % = 0,07; 7% = 7 : 100 = 0,07
32 % = 0,32; 32% = 32 : 100 = 0,32 1% - сотая часть числа
129 % = 1,29; 129% = 129 : 100 = 1,29
4,5% = 0,045; 4,5% = 4,5 : 100 = 0,045
Чтобы записать десятичную дробь в виде процентов, надо данное число умножить на 100
0,09 = 9 %; 0,09 = 0,09 100 = 9%
0,36 = 36 %; 0,36 = 0,36 100 = 36%
2,4 = 240 %; 2,4 = 2,4 100 = 240%
0,0278 = 2,78 %; 0,0278 = 0,0278 100 = 2,78%

 Получите свидетельство
Получите свидетельство Вход
Вход


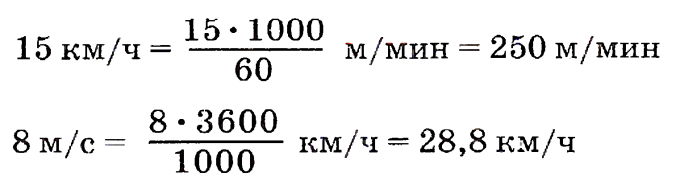

 +
+ 
 -
- 
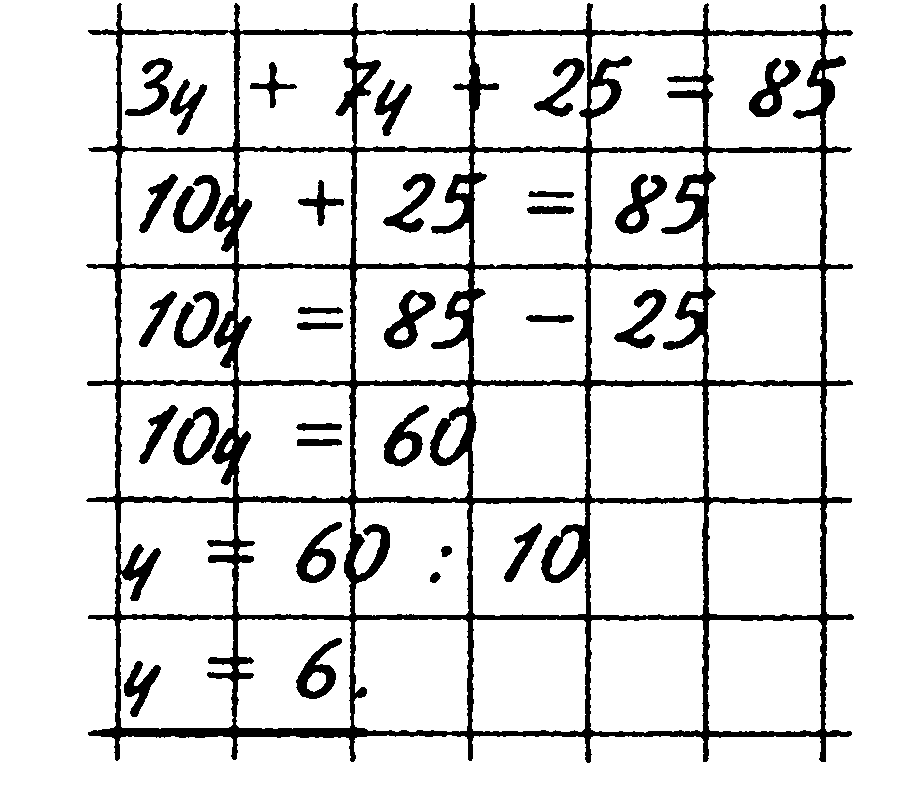
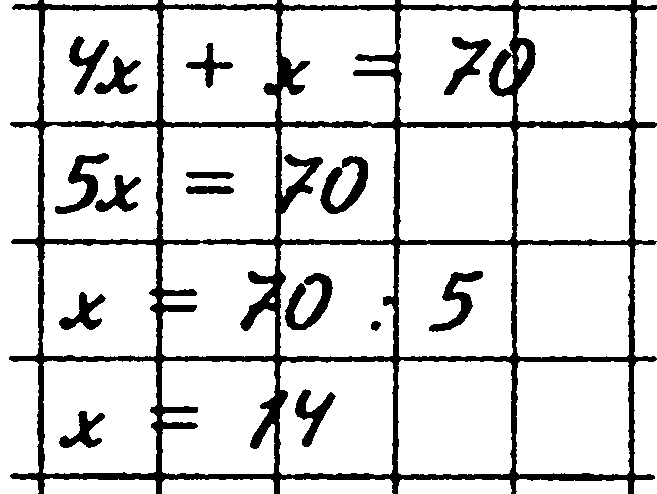




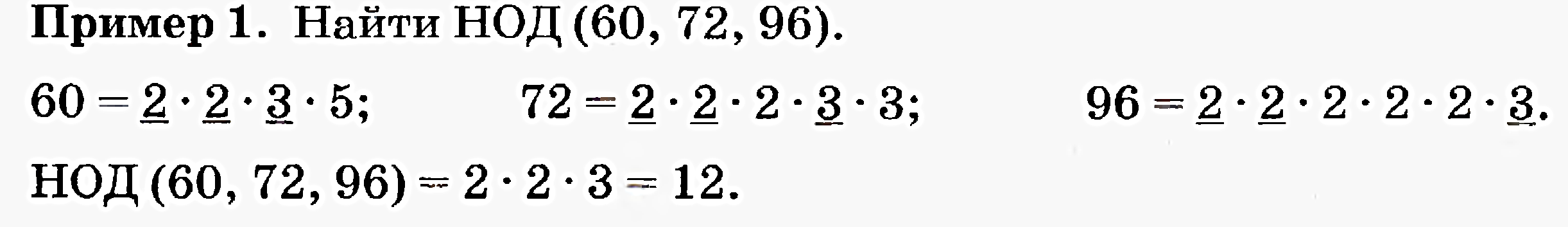




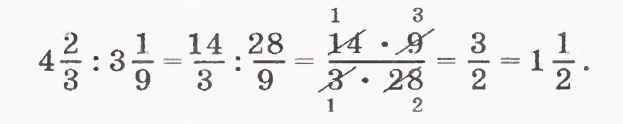
 АДАЧА 2
АДАЧА 2
 АДАЧА 3
АДАЧА 3


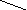




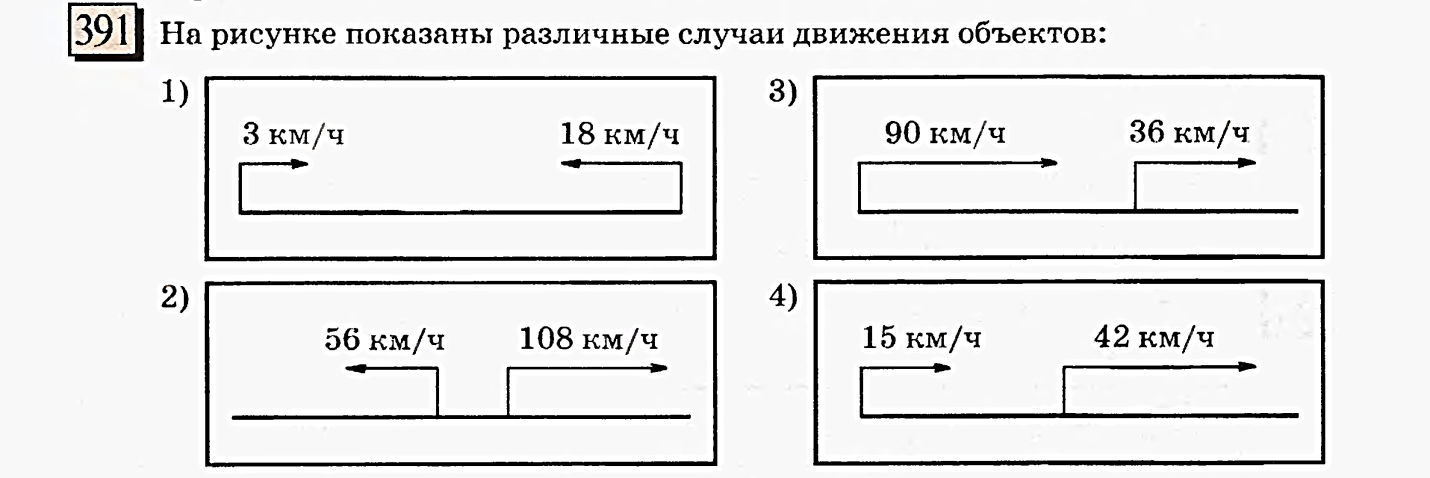

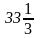
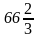
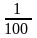
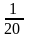
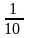
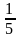

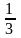

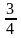
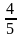










 Справочный материал к урокам математики (5 класс) (10.46 MB)
Справочный материал к урокам математики (5 класс) (10.46 MB)
 0
0 677
677 32
32 Нравится
0
Нравится
0







