Получите свидетельство
Вход
Проверяемые элементы содержания и виды деятельности:
умение анализировать различные возможности и выбирать наиболее оптимальную в зависимости от поставленных условий, умение решать текстовые задачи, составляя математическую модель предложенной в них ситуации, умение использовать приобретенные знания и умения в практической деятельности и повседневной жизни.
Ориентировочное время выполнения учащимися, изучающими математику на базовом уровне: 5—10 минут.
Типы заданий: Выбор оптимального варианта из двух возможных.
Внимание: особенности экзаменационных заданий.
Экзаменационные задания данного типа логически просты: следует перебрать все возможные варианты. Однако на экзамене не разрешается пользоваться микрокалькуляторами, а значит, есть вероятность допустить ошибку в вычислениях.
Проводите все расчеты письменно, записывайте выкладки аккуратно. Это позволит вам обнаружить возможные вычислительные ошибки при повторной проверке решений перед сдачей работы.
Это надо знать.
Для решения этого типа заданий необходимо уметь проводить вычисления с многозначными числами: складывать, вычитать, умножать и делить «в столбик».
Задача 1.
Вася загружает на свой компьютер из Интернета файл размером 30 Мб за 28 секунд. Петя загружает файл размером 28 Мб за 25 секунд, а Миша загружает файл размером 32 Мб за 29 секунд. Сколько секунд будет загружаться файл размером 420 Мб на компьютер с наибольшей скоростью загрузки?
Задача 2.
В среднем гражданин А. в дневное время расходует 125 кВтч электроэнергии в месяц, а в ночное время — 155 кВтч электроэнергии. Раньше у А. в квартире был установлен однотарифный счетчик, и всю электроэнергию он оплачивал по тарифу 2,4 руб. за кВтч. Год назад А. установил двухтарифный счeтчик, при этом дневной расход электроэнергии оплачивается по тарифу 2,4 руб. за кВтч, а ночной расход оплачивается по тарифу 0,7 руб. за кВтч.
В течение 12 месяцев режим потребления и тарифы оплаты электроэнергии не менялись. На сколько больше заплатил бы А. за этот период, если бы не поменялся счетчик? Ответ дайте в рублях.
Задача 3.
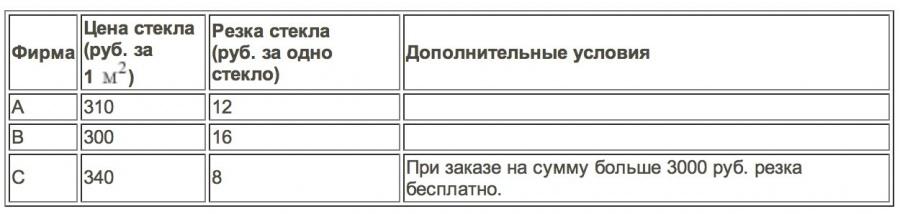
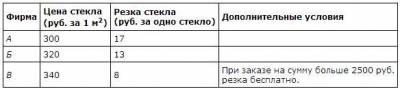
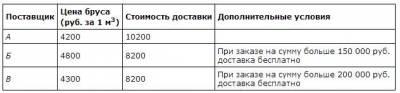
Для остекления музейных витрин требуется заказать 30 одинаковых стекол в одной из трех фирм. Площадь каждого стекла 0,3 м. В таблице приведены цены на стекло и на резку стекол. Сколько рублей будет стоить самый дешевый заказ?
Задача 4.
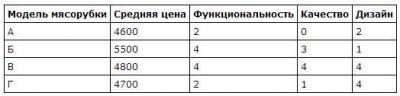
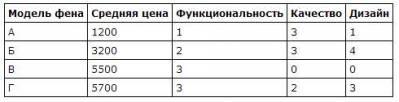
Рейтинговое агентство определяет рейтинг соотношения «цена-качество» микроволновых печей. Рейтинг вычисляется на основе средней цены P и оценок функциональности F, качества Q и дизайна D. Каждый отдельный показатель оценивается экспертами по 5-балльной шкале целыми числами от 0 до 4. Итоговый рейтинг вычисляется по формуле
R=8(F+Q) +4D-0,01P
В таблице даны оценки каждого показателя для нескольких моделей печей. Определите, какая модель имеет наивысший рейтинг. В ответ запишите значение этого рейтинга.
Задача 5.
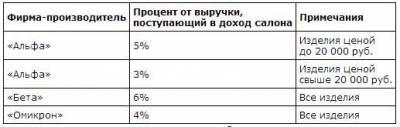
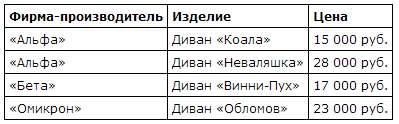
Мебельный салон заключает договоры с производителями мебели. В договорах указывается, какой процент от суммы, вырученной за продажу мебели, поступает в доход мебельного салона.
В прейскуранте приведены цены на четыре софы. Определите, продажа какой софы наиболее выгодна для салона. В ответ запишите, сколько рублей поступит в доход салона от продажи этой софы.
Задача 6.
В первом банке один евро можно купить за 39,2 рубля. Во втором банке 100 евро — за 3950 рублей. В третьем банке 30 евро стоят 1179 рублей. Какую наименьшую сумму (в рублях) придется заплатить за 10 евро?
Задача 7.
Своему постоянному клиенту компания сотовой связи решила предоставить на выбор одну из скидок. Либо скидку 20% на звонки абонентам других сотовых компаний в своем регионе, либо скидку 25% на звонки в другие регионы, либо 5% на услуги мобильного интернета.
Весь материал - в документе.
Справочные материалы для подготовки к ЕГЭ по математике "Задания B4: Выбор оптимального варианта" (0.14 MB)
0
580
65
Нравится
0
