Материал на украинском языке.
Мета. Навчати учнів знаходити спільні дільники кількох чисел. Формувати навички знаходження найбільшого спільного дільника за алгоритмом. Підвищувати рівень математичної культури. Розвивати логічне мислення учнів
Тип уроку. Урок засвоєння нових знань
Хід уроку
І. Забезпечення емоційної готовності
Учитель. Добрий день! Як настрій? Посміхніться один одному і побажайте удачі!
ІІ. Актуалізація опорних знань.
Учитель. Розшевелімо ваші сірі клітинки, пригадаймо дещо з попередніх уроків.
Фронтальне опитування
Яке число називають дільником даного числа?
Яке число називають простим?
Яке число називають складеним?
Учитель. Продовжимо активувати сірі клітинки. Візьміть сигнальні картки. Нагадаємо: зелена картка – правильна відповідь; червона – неправильна. Отож тест „Чи істинне твердження?”. В картці самоконтролю під час тестування відмічайте правильність своїх відповідей + або -.
Тест
Просте число має тільки два дільники.
Складене число має один дільник.
Число 5 є дільником числа 24.
Число 12 є дільником числа 6.
Число 7 – просте.
Число 25 – просте.
Число 10 – складене.
Число 1 – просте.
Найменше двоцифрове просте число 11.
Деякі складені числа не можливо розкласти на прості множники.
Розклад числа на прості множники виконаний правильно.
ІІІ. Повідомлення теми уроку. Постановка цілей уроку
Учитель. Ми не дарма пригадали з вами саме цей матеріал. Сьогодні на уроці ми його використаємо для вивчення нової теми. Запишіть в зошитах число, класна робота.Тема уроку:
Слайд 5
Учитель. Діти, прочитавши тему уроку, скажіть, що нового ви зможете сьогодні дізнатися, навчитись робити?
Дізнатись: що таке спільний дільник кількох чисел, що таке НСД; які числа називають взаємно простими.
Навчитись: визначати спільні дільники; взаємно прості числа; знаходити НСД.
ІV. Мотивація. Створення проблемної ситуації
Учитель. Уявіть таку ситуацію. У вас день народження. За традицією вашого класу, ви збираєтесь пригостити однокласників. Мама купила два сорти цукерок: І сорту виявилось 84 цукерки, ІІ – 56. Постають питання:
Скільки однакових подарунків можна скласти з цукерок, що купила мама?
Яку найбільшу кількість однакових подарунків можна скласти?
Чи зможете ви всіх однокласників пригостити однаковими подарунками?
V. Формування та засвоєння нових знань
Учитель. Яким чином ми можемо дати відповідь на І запитання? Спочатку проаналізуємо, скільки подарунків можна зробити з цукерок І сорту? Знаходимо дільники числа 84.
Учитель. Далі знаходимо дільники числа 56.
Учитель. Знайдемо, які є однакові дільники. Це і є спільні дільники чисел 84 і 56.
Учитель. Відповімо на ІІІ запитання. Чудовий збіг! Як раз 28 учнів у вашому класі! Такий метод знаходження НСД називається за означенням НСД.
Прочитаємо означення в підручнику на сторінці 25.
Цей метод не єдиний із відомих.
В картку самоконтролю учні ставлять + або – про правильність виконання завдань.
Роблять висновок, визначаючи для себе істинність одного з наступних тверджень:
Я зрозумів, як знаходити НСД чисел.
Я знаю, як знаходити НСД чисел, але ще допускаю помилки.
Я не зрозумів, як знаходити НСД чисел.
VІІІ. Підсумок уроку.
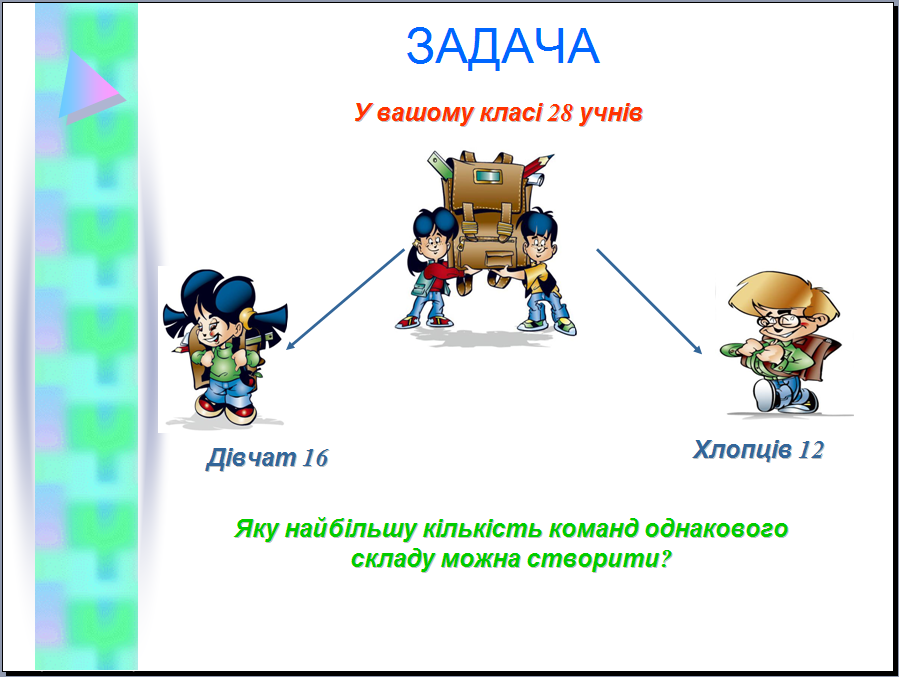
Задача. На уроці фізичної культури проводяться змагання. Допоможіть вчителю. Якщо в вашому класі 28 учнів: 16 дівчат і 12 хлопців, то яку найбільшу кількість команд однакового складу можна створити?
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход




 читель. Продовжимо активувати сірі клітинки. Візьміть сигнальні картки. Нагадаємо: зелена картка – правильна відповідь; червона – неправильна. Отож тест „Чи істинне твердження?”. В картці самоконтролю під час тестування відмічайте правильність своїх відповідей + або -.
читель. Продовжимо активувати сірі клітинки. Візьміть сигнальні картки. Нагадаємо: зелена картка – правильна відповідь; червона – неправильна. Отож тест „Чи істинне твердження?”. В картці самоконтролю під час тестування відмічайте правильність своїх відповідей + або -.

 читель. Тепер оцініть, будь ласка, свою роботу.
читель. Тепер оцініть, будь ласка, свою роботу.  читель. Ми не дарма пригадали з вами саме цей матеріал. Сьогодні на уроці ми його використаємо для вивчення нової теми. Запишіть в зошитах число, класна робота.Тема уроку:
читель. Ми не дарма пригадали з вами саме цей матеріал. Сьогодні на уроці ми його використаємо для вивчення нової теми. Запишіть в зошитах число, класна робота.Тема уроку: и зможете ви всіх однокласників пригостити однаковими подарунками?
и зможете ви всіх однокласників пригостити однаковими подарунками?


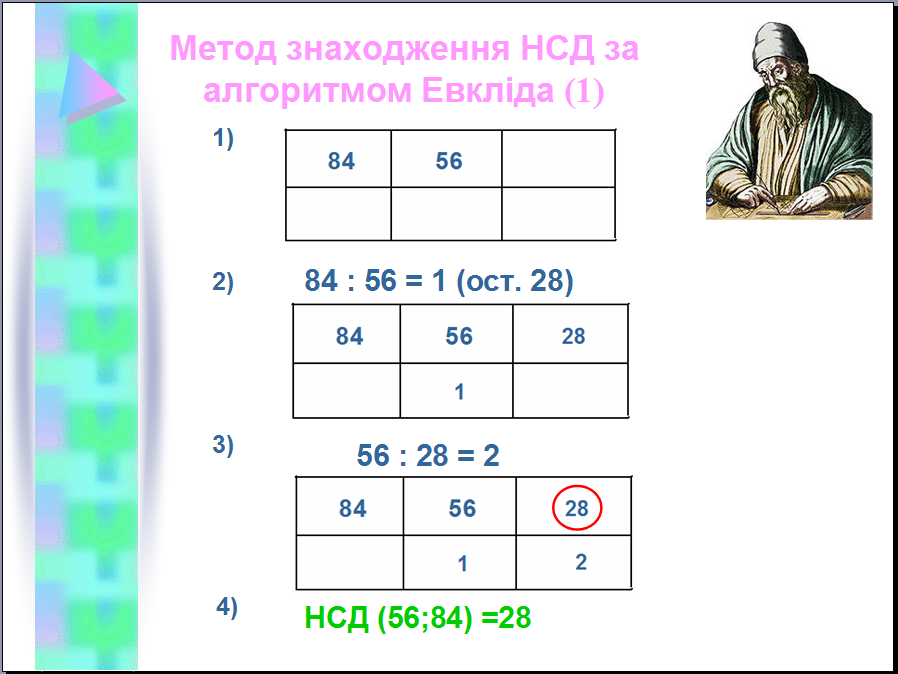
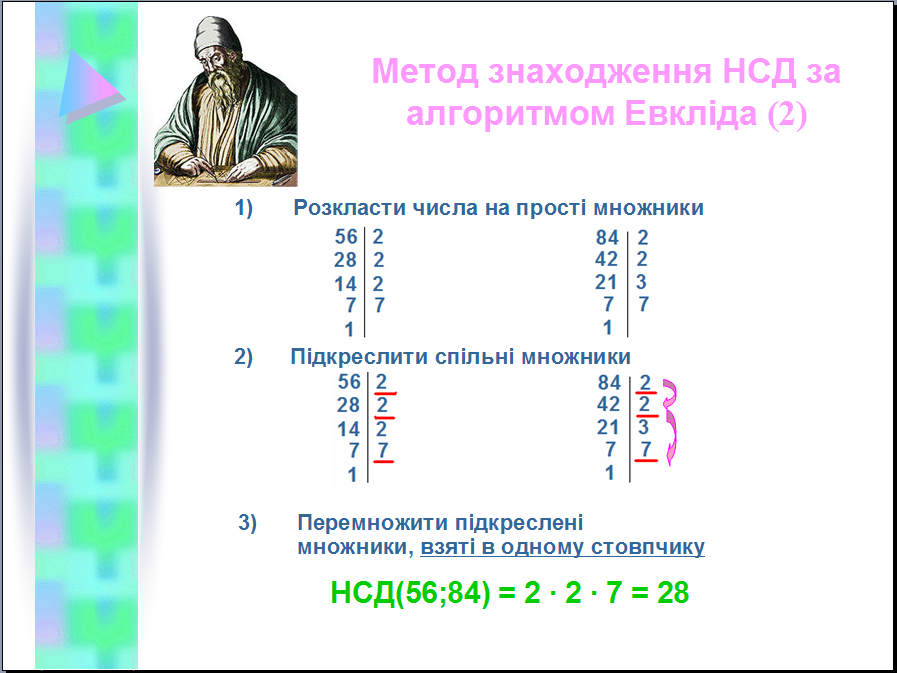
 читель. Яке найбільше з цих чисел? 28. Ось і відповідь на ІІ запитання. НСД (56;84) = 28.
читель. Яке найбільше з цих чисел? 28. Ось і відповідь на ІІ запитання. НСД (56;84) = 28.


 авдання 1
авдання 1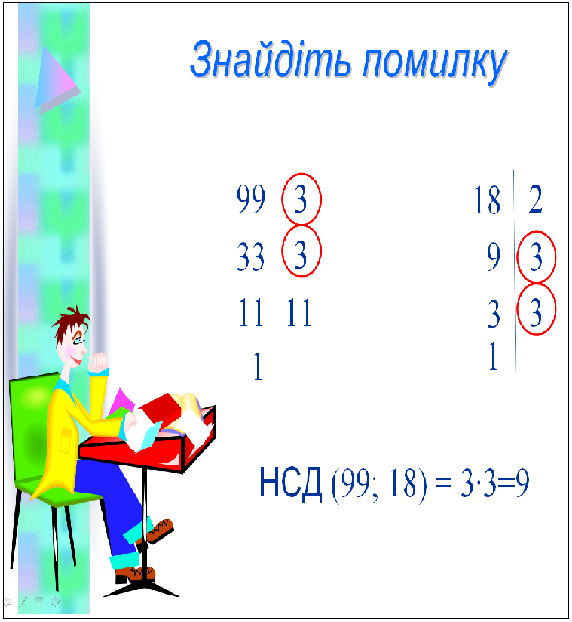
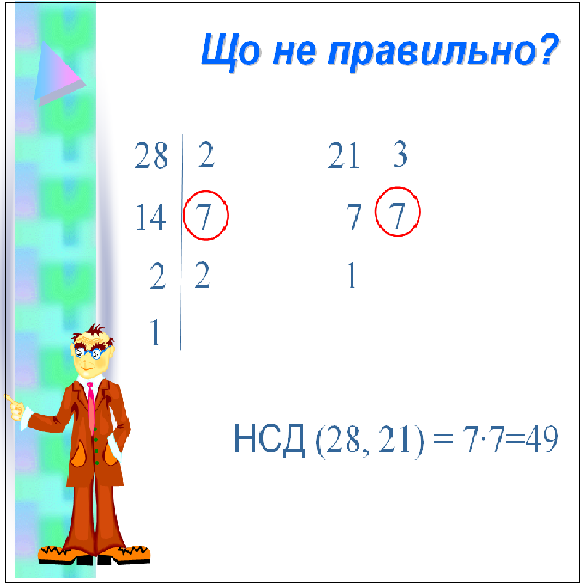 авдання 2.
авдання 2.  ідповідь:
ідповідь: озв’язування вправ.
озв’язування вправ.











 Спільний дільник кількох чисел. Найбільший спільний дільник. Взаємно прості числа (4.45 MB)
Спільний дільник кількох чисел. Найбільший спільний дільник. Взаємно прості числа (4.45 MB)
 0
0 851
851 89
89 Нравится
0
Нравится
0


