Сопряжение линий

Министерство образования и науки Республики Дагестан

Государственное бюджетное профессиональное образовательное учреждение Республики Дагестан

«Колледж архитектуры и строительства»

Открытый урок

по черчению на тему:

«Сопряжение линий»

Разработала: Шамсудинова М.В.

преподаватель спецдисциплин

2019г.

Тема урока: Сопряжение линий.

Цель урока:

1. Образовательная

- Формирование новых понятий.

- Углубление знаний.

- Систематизация обобщения знаний.

2. Развивающая

- Развитие творческого мышления.

- Развитие умений и навыков работы с чертежными

инструментами.

- Формирование качеств творческой личности.

-Интерес к народному творчеству

3. Воспитательная

- Показ важности изучаемой темы.

- Показ значимости приобретенных знаний.

- Формирование умений осуществлять контроль.

- Воспитать аккуратность, четкость, самостоятельность

выполнения работы

Оборудование для учащихся:

тетради, чертежные инструменты, карточки-задания, учебник, формат А4

для преподавателя: учебник, чертежные инструменты, проектор, интерактивная доска, презентации с примерами по теме.

План урока

1. Организационная часть (2 минуты)

2. Повторение пройденного материала (5 минут)

3. Изложение нового материала (45 минут)

4. Закрепление пройденного на уроке (35минут)

5. Итог урока. Задание на дом (3 минут)

Ход урока

1. Организационная часть

Приветствие ребят. Выявление отсутствующих.

2.Повторение пройденного материала «Геометрические построения»

Фронтальный опрос: (задание на карточках с заранее вычерченными окружностями)

1-й вариант - задание: разделить окружность на 4 равных части;

2-й вариант - разделить окружность на 3 равные частей.

Сдача работ 1 и 2-го варианта и проверка чертежей через изображения на мониторе.

Демонстрируются наиболее яркие и простые примеры использования сопряжений в технике, архитектуре, дизайне и т.д. (презентация «Сопряжения в окружающей среде»).

Затем сами учащиеся приводят аналогичные примеры из их быта и жизненного опыта.

3. Изложение нового материала

Сегодня на уроке мы познакомимся с сопряжениями линий.

На карточках даны детали, рассмотрите их и дайте ответы на вопросы.

- Сравните форму данных деталей и скажите, чем они отличаются друг от друга?

- Посмотрите на чертежи подобных деталей и скажите, чем они отличаются друг от друга?

- Какое из этих изображений вы могли бы построить прямо сейчас?

- При помощи какого чертежного инструмента можно построить округления углов?

Плавные переходы линий встречаются при моделировании одежды, когда строится выкройка; в чертежах деталей, в орнаментах различных народов; в украшениях и т.д.

Определение:

Плавный переход одной линии в другую называется сопряжением.

Где применяется сопряжение?

Сопряжение применяется для того, чтобы построить контур технической детали, (показ двух технических деталей), где можно наблюдать плавные переходы одной поверхности в другую. Для того чтобы построить чертежи данных деталей, необходимо знать способы построения сопряжений. Плавные переходы одной поверхности в другую на технических деталях применяются для того, чтобы повысить стойкость и увеличить прочность, уменьшить травмоопасность.

Плавные переходы одной поверхности в другую применяют в эстетических целях. (Показ предметов с красивыми контурными линиями).

Говоря о красоте плавных линий, нельзя не сказать о том, что они применяются в архитектуре.

Я думаю, что убедила вас в том, что знание способов построения сопряжений линий необходимо.

Сначала мы рассмотрим сопряжение прямых линий, когда они располагаются под прямым углом, под острым углом и под тупым углом.

Рассмотрим элементы сопряжений на примере построения сопряжения тупого угла, причем стороны угла называются сопрягаемыми линиями.

Сопряжение – это плавный переход одной линии в другую.

Общий алгоритм построения сопряжения:

1. Необходимо найти центр сопряжения.
2. Необходимо найти точки сопряжения.
3. Построить сопряжение (плавный переход одной линии в другую)
3. 3.1. Построение сопряжения двух сторон угла окружности заданного радиуса.

Сопряжение двух сторон угла (острого и тупого) дугой заданного радиуса R выполняют следующим образом:

Параллельно сторонам угла на расстоянии, равном радиусу дуги R, проводят две вспомогательные прямые линии. Точка пересечения этих прямых (точка О) будет центром дуги радиуса R, т.е центром сопряжения . Из точки О описывают дугу, плавно переходящую в прямые – стороны угла. Дугу заканчивают в точках сопряжения n и n1, которые являются основаниями перпендикуляров, опущенных из центра О на стороны угла. При построении сопряжения сторон прямого угла центр дуги сопряжения проще находить с помощью циркуля. Из вершины угла А проводят дугу радиусом R до взаимного пересечения в точке О, являющейся центром сопряжения. Из центра О описывают дугу сопряжения. Построение сопряжения двух сторон угла показано на рис.1.

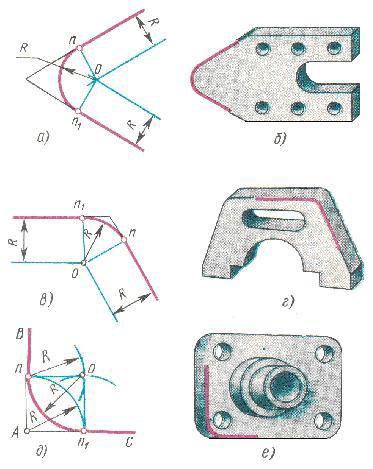
Рис. 1

Сопряжение – это плавный переход одной лини в другую.

Общий алгоритм построения сопряжения:

1. Необходимо найти точку сопряжения.
   2. Необходимо найти точки сопряжения.
   3. Построение сопряжения (плавного перехода одной линии в другую).

3.3.2 Построение внутреннего и внешнего сопряжения между прямой и дугой окружности.

Сопряжение прямой с дугой окружности может быть выполнено при помощи дуги с внутренним касанием дуги и внешним касанием. На рисунке 2(а, б) показано сопряжение дуги окружности радиусом Rи прямой линии АВ дугой окружности радиуса r с внешним касанием. Для построения такого сопряжения проводят окружность радиуса R и прямую АВ. Параллельно заданной прямой на расстоянии, равному радиусу r (радиус сопрягающей дуги), проводят прямую ab. Из центра О проводят дугу окружности радиусом, равным сумме радиусов R и r, до пересечения ее с прямой ab в точке О1. Точка О1 является центром дуги сопряжения. Точку сопряжения с находят на пересечении прямой ОО1 с дугой окружности радиуса R. Точка сопряжения О1 на данную прямую АВ. При помощи аналогичных построений могут быть найдены точки О2, с2, с3. На рисунке 2(а, б) показан кронштейн, при вычерчивании которого необходимо выполнить построения, описанные выше.

Рис. 2

При вычерчивании маховика, выполнено сопряжение дуги радиуса R с прямой АВ дугой радиуса r с внутренним касанием. Центр дуги сопряжения О1 находится на пересечении вспомогательной прямой, проведенной параллельно данной прямой на расстоянии r, с дугой вспомогательной окружности, описанной из центра О радиусом, равным разности R-r. Точка сопряжения с 1 является основанием перпендикуляра, опущенного из точки О1 на данную прямую. Точку сопряжения с находят на пересечении прямой ОО1 с сопрягаемой дугой. Пример построения сопряжения прямой с дугой окружности показан на рисунке 3.

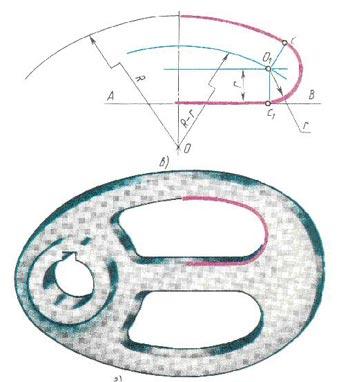
Рис. 3

Сопряжение – это плавный переход одной лини в другую.

Общий алгоритм построения сопряжения:

1. Необходимо найти центр сопряжения.
2. Необходимо найти точки сопряжения.
3. Построение линии сопряжения (плавного перехода одной лини в другую).

3.3.3. Построение сопряжения между двух дуг окружностей.

Сопряжение двух дуг окружностей может быть внутреннее и внешнее.
При внутреннем сопряжении центры О и О1 сопрягаемых дуг находятся внутри сопрягающей дуги радиуса R. При внешнем сопряжении центры О и О1 сопрягаемых дуг радиусов R1 и R2 находятся вне сопрягающей дуги радиуса R.
Построение внешнего сопряжения:

Задано:

а) радиусы сопрягаемых окружностей R и R1;
б) расстояния между центрами этих дуг;
в) радиус R сопрягающей дуги;

Требуется:

а) определить положение центра О2 сопрягающей дуги;
б) найти точки сопряжения s и s1;
в) провести дугу сопряжения;

Построение внутреннего сопряжения:

Показано на рисунке 4(б) . По заданным расстояниям между центрами на чертеже намечают центры О и О1, из которых описывают сопрягаемые дуги радиусов R и R1. Из центра О1 проводят вспомогательную дугу окружности радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой дуги R2, а из центра О – радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой дуги R1. Вспомогательные дуги пересекутся в точке О2, которая и будет искомым центром сопрягающей дуги. Для нахождения точек пересечения продолжения прямых О2О и О2О1 с сопрягаемыми дугами являются искомыми точками сопряжения (точки s и s1).

Построение внутреннего сопряжения:

Задано:

а) радиусы R и R1 сопрягаемых дуг окружностей;
б) расстояния между центрами этих дуг;
в) радиус R сопрягающей дуги;

Требуется:

а) определить положение О2 сопрягающей дуги;
б) найти точки сопряжения s и s1;
в) провести дугу сопряжения;

Построение внешнего сопряжения показано на рисунке 4(в). По заданным расстояниям на чертеже находят точки О и О1, из которых описывают сопрягаемые дуги радиусов R1 и R2. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги R2 и сопрягающей R. Вспомогательные дуги пересекутся в точке О2, которая будет искомым центром сопрягающей дуги. Для нахождения точек сопряжения центры дуг соединяют прямыми линиями ОО2 и О1О2. Эти две прямые пересекают сопрягаемые дуги в точках сопряжения s и s1. Из центра О2 радиусом Rпроводят сопрягающую дугу, ограничивая ее точками S и S1.

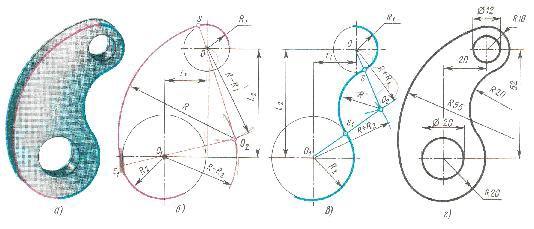
Рис. 4

3.3.4. Построение смешанного сопряжения.

Пример смешанного сопряжения показан на рисунке 5.

Задано:

а) Заданы радиусы R и R1 сопрягаемых дуг сопряжения;
б) расстояния между центрами этих дуг;
в) радиус R сопрягающей дуги;

Требуется:

а) определить положение центра О2 сопрягающей дуги ;
б) найти точки сопряжения s и s1;
в) провести дугу сопряжения;

По заданным расстояниям между центрами на чертеже намечают центры О и О1, из которых описывают сопрягаемые дуги радиусов R1 и R2. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги R1 и сопрягающей R, а из центра О1 – радиусом, равным разности радиусов R и R2. Вспомогательные дуги пересекутся в точке О2, которая будет искомым центром сопрягающей дуги. Соединив точки О и О2 прямой, получают точку сопряжения s1; соединив точки О1 и О2, находят точку сопряжения s. Из центра О2 проводят дугу сопряжения от s до s1. На рисунке 5 показан пример построения смешанного сопряжения.

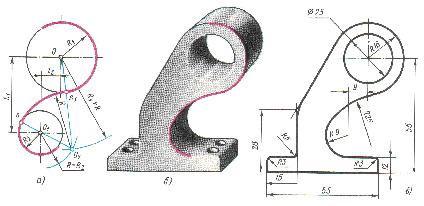
Рис. 5

4. Закрепление пройденного материала на уроке.

- Как и в предыдущей теме, здесь очень важны ли­нии построения: можно сказать, что они не менее важны, чем сам чертеж. Обязательно отмечайте три элемента сопряжения. (Уча­щиеся называют эти элементы.) Выполняйте построение точно по алгоритму.

Для закрепления пройденного материала необходимо выполнить практическую работу.

Выполнить чертеж детали, применив правила сопряжений. Линии сопряжений на чертеже сохранить. При работе обратите внимание на алгоритм выполнения чертежей.

-Если деталь симметрична, с чего начинаем выполнять чертеж?

Выполняя чертеж, не забывайте о типах линий.

Приступаем к работе. Во время работы учащихся необходимо следить за ходом выполнения данного задания, помогать тем, у кого будут вопросы.

5. Подведение итогов самостоятельной работы учащихся в группе

Оценка работы учеников.

Итог урока.

Домашнее задание.