Тема урока: Соотношения между сторонами и углами прямоугольного треугольника.
Цели урока: Систематизировать и обобщить знания и умения учащихся по данной теме; показать метапредметные связи, использование материала вне урока; расширить кругозор учащихся; подготовить к контрольной работе.
Повышать интерес математике посредством нестандартных форм проведения урока; пропедевтика готовности к сдаче экзаменов в форме ЕГЭ.
Прививать навыки само и взаимоконтроля; воспитывать сознательное отношение к учёбе.
Тип урока: обобщение и систематизация знаний и умений.
Вид урока: смотр знаний.
Оборудование: листы с заданиями, таблицами для заполнения значений тригонометрических выражений, сводная таблица результатов, компьютер, проектор, интерактивная доска, карточки для рефлексии.
Ход урока
I. Организационная часть
Вступительное слово учителя о теме и форме проведения урока. Заключительный урок по теме учитель предлагает провести смотр знаний в виде «показательных выступлений». Но в отличии спортивных выступлений, наши, всё таки, будут оцениваться, и учащиеся имеют возможность получить по две оценки: одна будет складываться из ответов в течение урока, другая из выполненных заданий самостоятельной работы в формате ЕГЭ.
II. Актуализация опорных знаний
Для участия в выступлениях желательно «подать заявку», получив за это дополнительный балл, которая представляет собой любое теоретическое утверждение о прямоугольном треугольнике. Балл заносится в сводную таблицу.
Так же некоторые учащиеся знакомят с заранее подготовленной информацией о происхождении названий сторон прямоугольного треугольника и основных тригонометрических выражений. Сообщения оцениваются в один балл.
III. Межпредметная связь. Словарный диктант
Так как олимпиада проходила в нашей стране и государственным языком является русский язык, то участникам необходимо пройти небольшой тест на знание русского языка. Проверка словарного диктанта выполняется самостоятельно по готовым записям самими учащимися. Полученные баллы заносятся в таблицу.
Планиметрия, геометрия, подобие, противолежащий, треугольник, тангенс, прилежащий, высота, гипотенуза, синус, равнобедренный, катет, прямоугольный, косинус, тригонометрия.
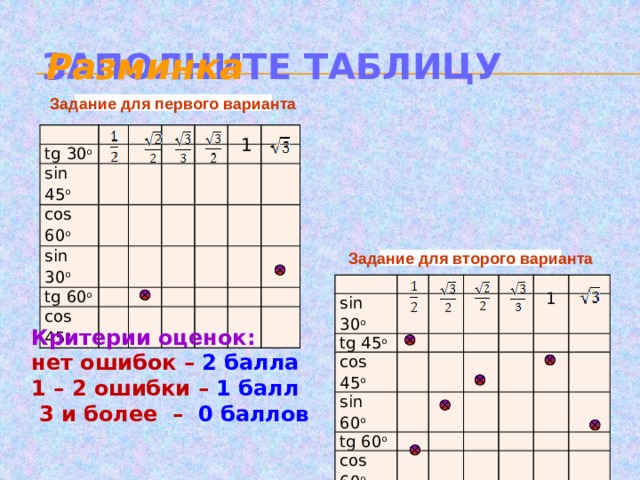
IV. Разминка. Проверка знаний значений тригонометрических выражений для некоторых углов
Перед началом выступлений необходима разминка, для этого учащиеся по вариантам выполняют задание в готовых таблицах на знание значений синуса, косинуса и тангенса некоторых углов. Работа выполняется по вариантам, по готовым ответам проводится взаимопроверка, и выставление полученных баллов. Баллы заносятся в таблицу. Проверенные работы сдаются учителю.
|
|
|
|
|
| 1 |
|
| tg 30o |
|
|
|
|
|
|
| sin 45o |
|
|
|
|
|
|
| cos 60o |
|
|
|
|
|
|
| sin 30o |
|
|
|
|
|
|
| tg 60o |
|
|
|
|
|
|
| cos 45o |
|
|
|
|
|
|
|
|
|
|
|
| 1 |
| |
| sin 30o |
|
|
|
|
|
| |
| tg 45o |
|
|
|
|
|
| |
| cos 45o |
|
|
|
|
|
| |
| sin 60o |
|
|
|
|
|
| |
| tg 60o |
|
|
|
|
|
| |
| cos 60o |
|
|
|
|
|
| |
А теперь, ребята, встали,
Быстро руки вверх подняли,
В стороны, вперёд, назад,
Повернулись вправо, влево,
Тихо сели, вновь за дело.
VI. Зачётное соревнование. Самостоятельная работа в два варианта в формате ЕГЭ.
Учащиеся получают листы с заданиями, в которых имеется четыре задания с выбором ответа, два с кратким ответом и два с развернутым решением. Задания выполняются в тетрадях, ответы заносятся в подготовленные таблицы на отдельных листах, там же выполняются задания с развёрнутым решением. На работу отводится 20 минут, после чего сдаются ответы с решениями, а учащиеся проверяют самостоятельно по предложенной таблице правильность своих решений. Заданий предлагается достаточное количество, поэтому ребёнок может выбрать посильное для него упражнение. Окончательные результаты по данному виду работы учащиеся получат на следующем уроке после его проверки задания с развёрнутым решением.
Вариант 1
А1. В треугольнике АВС  С = 90°,
С = 90°, 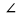 А = 41°, ВС = 5 см.
А = 41°, ВС = 5 см.
Найдите длину АС.
1) 5 · соs41° 2) 5 : tg41° 3) 5 · tg41° 4) 5 : siп41°
А2. siпα = 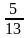 . Найдите tg
. Найдите tg 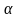 .
.
1) 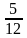 2)
2) 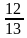 3)
3) 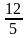 4)
4) 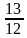
А3. В треугольнике КСР (КС = СР) 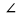 С = 68°, КС = 12 см.
С = 68°, КС = 12 см.
Найдите длину КР.
1) 12 · соs34° 2) 6 · соs34° 3) 24 · sin34° 4) 24 : siп34°
А4. Вычислите значение выражения sin260° – 3tg45°.
1) – 2,25 2) – 1,25 3) – 0,75 4) – 1,5
В1. В треугольнике АВС 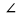 С = 90°, СD – высота,
С = 90°, СD – высота, 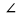 A =
A = 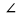 α
α
АВ = k. Найдите длины АС, ВС, АD.
В2. Стороны параллелограмма равны 4 см и 5 cм, угол между ними 45°. Найдите высоты параллелограмма.
С1. В прямоугольной трапеции меньшее основание равно 6, а меньшая боковая сторона – 2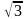 . Найдите площадь трапеции, если один из ее углов равен 120°.
. Найдите площадь трапеции, если один из ее углов равен 120°.
С2. В равнобедренном треугольнике АВС (АВ = ВС) 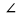 A = 30°. Найдите высоту, опущенную к основанию, если АD = 20 см (D
A = 30°. Найдите высоту, опущенную к основанию, если АD = 20 см (D 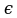 прямой АВ, СD
прямой АВ, СD 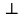 АВ).
АВ).
Вариант 2
А1. В треугольнике АВС  С = 90°,
С = 90°, 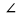 B = 49°, ВС = 9 см.
B = 49°, ВС = 9 см.
Найдите длину АС.
1) 9 : tg49° 2) 9 · cos49° 3) 9 : sin49° 4) 9 · tg49°
А2. cosα = 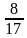 . Найдите tg
. Найдите tg 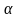 .
.
1) 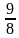 2)
2) 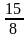 3)
3) 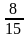 4)
4) 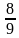
А3. В треугольнике CED (CD = DE) 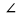 D = 78°, CE = 16 см.
D = 78°, CE = 16 см.
Найдите длину CD.
1) 8 · sin39° 2) 16 : sin78° 3) 8 · cos51° 4) 8 : siп39°
А4. Вычислите значение выражения cos245° – 4sin30°.
1) – 2 2) – 3 3) – 1,5 4) – 2,5
В1. В треугольнике MNP 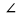 P = 90°, PK – высота,
P = 90°, PK – высота, 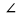 N =
N = 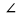 β
β
PN = b. Найдите длины MN, MP, KN.
В2. Стороны параллелограмма равны 6 см и 7 cм, угол между ними 60°. Найдите высоты параллелограмма.
С1. В равнобедренной трапеции меньшее основание равно 8, а меньшая боковая сторона – 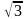 . Найдите площадь трапеции, если один из ее углов равен 150°.
. Найдите площадь трапеции, если один из ее углов равен 150°.
С2. В равнобедренном треугольнике АВС с основанием АС угол при вершине равен 120°, CD – высота. Найдите длину АD, если высота, проведённая к основанию, равна 10 см.
|
| А1 | А2 | А3 | А4 |
В1 | В2 | С1 | С2 |
| Вариант 1 | 2 | 1 | 3 | 1 | AC = k · cosα BC = k · sinα AD = k · cos2α |
|
14
| 30 |
| Вариант 2 | 4 | 2 | 3 | 1 | MN = b : cosβ MP = b · tgβ KN = b · cosβ | 3 3,5 | 11 | 30 |
VII. Применение полученных знаний в других областях. В гостях у «Кенгуру».
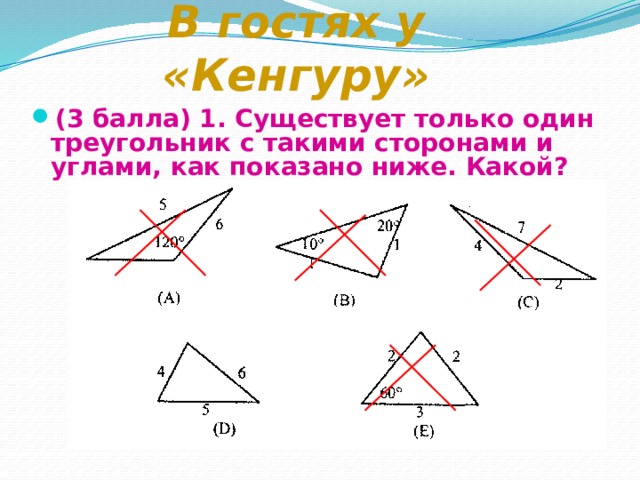
Как и олимпиада, наши выступления принимают международный размах, тем более, что скоро будет проходить математический конкурс-игра «Кенгуру», поэтому предлагаю вам одно из заданий этого конкурса. Решивший получает дополнительный бал.
(3 балла) 1. Существует только один треугольник с такими сторонами и углами, как показано ниже. Какой? Ответ D
VIII. Рефлексия.
У учащихся имеются заготовленные бланки с вопросами, отражающими итоги сегодняшнего урока. Заполнив их и сдав учителю, они получат дифференцированное домашнее задание в электронный дневник с учётом возникших вопросов.
Узнали ли что-то новое?
Доволен ли я собой: а) да, могу помочь другому;
б) да, вполне;
в) не очень;
г) нет.
Укажите задания, вызвавшие затруднения.
IX. Домашнее задание:
Ответить на вопросы к главе VII на стр. 160; подготовиться к контрольной работе.
Индивидуальные задания в электронном журнале.

 Получите свидетельство
Получите свидетельство Вход
Вход



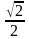
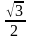
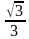


















 Смотр знаний по геометрии в 8 классе по теме "Прямоугольный треугольник" (344.02 KB)
Смотр знаний по геометрии в 8 классе по теме "Прямоугольный треугольник" (344.02 KB)
 0
0 117
117 6
6 Нравится
0
Нравится
0


