Математика – нескучная наука,
Математики – совсем не сухари!,
потому что в математике есть нечто, вызывающее восторг, и математика обладает не только истиной, но и величайшей красотой, и мы это сегодня докажем!
Так как вы ещё мало знакомы и, может быть, стесняетесь, доказательство начну Я!
Представляете, хоть я и люблю математику, но я всё ещё считаю на пальцах, хотите, научу вас умножать на 9
Пустяк! – скажете вы, но зато я могу находить квадраты двузначных чисел, оканчивающихся цифрой 5, устно! Ну, задавайте числа! Например, квадрат 35 -1225! 45 - 2025!..хотите, научу?
Что ж, тогда спрашивать буду я !
Вы отлично считаете? Подходите ближе!
Я вызову новый восторг – запросто устно сложу десять чисел Фибоначчи (каждое третье число-это сумма двух предыдущих). Итак, вы выбираете два любых числа. Складывая, получаете третье, четвёртое,...десятое. Потом столбиком проверяете мой ответ, ведь я, не дожидаясь вас, его выдам! Раскрою секрет и сейчас.
А умеете ли Вы умножать на 11? Вот так это делается:
23·11=253
Это всё истина, но есть в математике и ложь, приводящая нас в восторг. Я легко докажу, что 5=6!
35+10-45=42+12-54 верно?
5*(7+2-9)=6*(7+2-9) верно?
Разделим на выражение в скобках и получим 5=6!
Перед нами математический софизм!- такое рассуждение, в котором неправильные предпосылки выдаются за истинные, в результате чего мы приходим к нелепым умозаключениям.
Здесь заведомо допускается замаскированная ошибка, которая приводит к абсурду. Так, где же она?
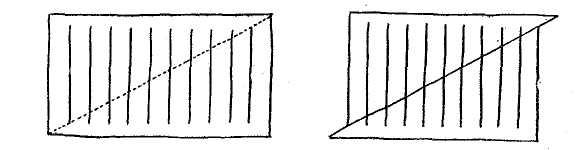
Или это! Перед вами прямоугольник с палочками, сколько их?
10!
Теперь разрежьте по линии и передвиньте на ширину расстояния между палочками - считайте их! Одна палочка бесследно растворилась в 9 остальных, удлинив каждую из них на одну девятую своей длины – совсем незаметное удлинение даёт неплохой эффект.
Такой же эффект даёт круг с палочками, надо только вращать, и палочка бесследно исчезает.
И, наконец, остроумная игрушка – задача. На арене цирка, по краю которой, художник разместил 13 клоунов в весьма воинствующих позах – внутренний круг вращайте по стрелке – уничтожился один из клоунов – их теперь 12.
Следующая практическая работа приведёт вас тоже в восторг.
Возьмём полоску бумаги и склеим, но предварительно перекрутив на полоборота один конец. Теперь покрасим внешнюю поверхность.
Вас очень удивит результат!
Вы заметили, что у этого кольца нет внутренней поверхности.
А называется она – лист Мёбиуса. Односторонняя поверхность – как рубашка без изнанки. Если по обычному кольцу паук, расположенный с одной стороны никогда не догонит муху, расположенную на другой стороне кольца, то здесь как раз наоборот – как бы не старалась муха, конец её неизбежен.
Открыть свой лист Мёбиусу помогла служанка, сшившая неправильно концы ленты. Интересно то, что почти одновременно независимо друг от друга одностороннюю поверхность открыли два немецких математика, оба ученика К.Ф.Гаусса – Август Фердинант Мёбиус и Иоганн Бенедикт Листинг.
А не хотите поэкспериментировать? Склейте концы ленты, перекрутив на полный оборот, на два оборота, сделайте разрез на одном конце ленты, просуньте в него другой конец и склеивайте по-разному. Красьте всякий раз и расскажите всем – что у вас получилось! А ещё попробуйте разрезать ровно пополам, на три части, на две разные, например 1/2. Я очень люблю эксперименты, уверена, что и вам понравится! Вот в чём вся прелесть – у вас будут появляться иногда два кольца- отдельные, иногда два, сплетённые друг с другом. О, это целая отдельная глава, и писать её уже вам. До встречи, друзья!

 Получите свидетельство
Получите свидетельство Вход
Вход




 потому что в математике есть нечто, вызывающее восторг, и математика обладает не только истиной, но и величайшей красотой, и мы это сегодня докажем!
потому что в математике есть нечто, вызывающее восторг, и математика обладает не только истиной, но и величайшей красотой, и мы это сегодня докажем!






 десь заведомо допускается замаскированная ошибка, которая приводит к абсурду. Так, где же она?
десь заведомо допускается замаскированная ошибка, которая приводит к абсурду. Так, где же она? 
 10!
10! Такой же эффект даёт круг с палочками, надо только вращать, и палочка бесследно исчезает.
Такой же эффект даёт круг с палочками, надо только вращать, и палочка бесследно исчезает.











 Скучная ли наука математика? (0.37 MB)
Скучная ли наука математика? (0.37 MB)
 0
0 628
628 129
129 Нравится
0
Нравится
0







