Курсовая работа
в рамках курсов повышения квалификации по теме «Систематизация заданий по решению систем уравнений второй части ОГЭ, конструирование подготовительных упражнений»
авторы:
Яковлева Марина Александровна, Пивоваров Дмитрий Владимирович, учителя математики МБОУ «СОШ №1 г.Тосно с углубленным изучением отдельных предметов»
2017г.
Содержание:
Введение
Анализ интернет ресурсов, решение системы
Цепочка вспомогательных задач
Анализ учебников по математике
Диагностика знаний учащихся 9 классов
Вывод
Введение:
Решение систем линейных алгебраических уравнений — одна из классических задач линейной алгебры, во многом определившая её объекты и методы. Кроме того, линейные алгебраические уравнения и методы их решения играют важную роль во многих прикладных направлениях.
Объект исследования: готовность учащихся к сдаче экзамена в форме ОГЭ
Предмет исследования: системы уравнений второй части ОГЭ
Цель исследования: выбрать системы уравнений второй части ОГЭ, разработать цепочку подготовительных задач, проанализировать учебники за 5-9 классы на наличие в них этих задач, рассмотреть методы решения.
2. Анализ интернет ресурсов, решение системы
Проведя анализ различных интернет-ресурсов, выяснили, что ОГЭ по математике часто в задании №21 содержат системы уравнений, также задания №22 (текстовая задача) иногда решается при помощи систем уравнений, решая которые учащиеся испытывают некоторые сложности.
Примеры таких систем приведены ниже:
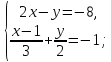 ответ: (-3,5;1)
ответ: (-3,5;1)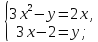 ответ: (
ответ: (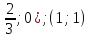
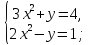 ответ: (1;1);(-1;1)
ответ: (1;1);(-1;1)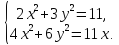 ответ: (2;1);(2;-1)
ответ: (2;1);(2;-1)
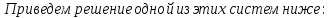
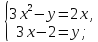
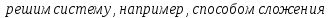 . Для этого перенесем в левую часть уравнений все слагаемые. Умножим второе уравнение на (-1). Получим:
. Для этого перенесем в левую часть уравнений все слагаемые. Умножим второе уравнение на (-1). Получим:
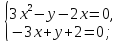
Выполним сложение, 2 уравнение перепишем, получим:
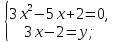
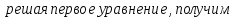 :
:
x1=1, х2=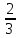 , подставляя в систему, найдем y, получим:
, подставляя в систему, найдем y, получим:
ответ: (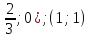
3. Для решения подобных систем составим цепочку вспомогательных задач:
Решение линейного уравнения (перенос слагаемых, рассуждения)
Приведение подобных слагаемых (правила раскрытия скобок, применение распределительного свойства)
Решение квадратного уравнения (использование различных способов)
Решение системы линейных уравнений способом подстановки
Решение системы линейных уравнений способом сложения
4. Анализ учебников по математике
Проведение анализа учебников математики и алгебры с 5 по 9 классы на предмет содержания в них необходимых задач выявил следующее:
5-6 класс (Н.Я. Виленкин): понятия систем не введено, решаются линейные уравнения: 5 класс по правилам: слагаемое+слагаемое+сумма, уменьшаемое-вычитаемое=разность, множитель*множитель=произведение, делимое:делитель=частное, 6 класс: по новым правилам решения уравнений (перенос выражения из одной части уравнения в другую…)
7 класс ( Ю.Н.Макарычев и др.под ред. С.А.Теляковского)
Вводится понятие систем уравнений и некоторые способы их решения.
| №1 |
|
|
|
|
| Решение методом подстановки. Для того чтобы решить систему уравнений методом подстановки нужно следовать простому алгоритму:
Ответ: (
| Решение методом сложения. Чтобы решить систему методом почленного сложения (вычитания) нужно:
-5x+5y+5x+2y=-5+16; 7y=11;
Ответ: (
|
| №2 |
|
| | |
| Решение методом подстановки.
; ; ; ; Ответ: (
| Решение методом сложения.
-2x-6x-y+y=-12-7;
Подставиим найденную переменную в первое уравнение:
Ответ: (
|
| №3 |
|
| Начальные преобразования (общие для обоих методов). | |
| Решение методом подстановки. ; ; ;
Ответ: (7;1)
| Решение методом сложения. + -2x+38y+12x-38y=24+46; 10x=70; x=7 Подставиим найденную переменную в первое уравнение: 7-19y=-12; y=1 Ответ: (7;1)
|
| №4 |
|
| Начальные преобразования (общие для обоих методов). ;
| |
| Решение методом подстановки.
; 5x=-36; x= y= Ответ: (-7,2;3,2)
| Решение методом сложения. + 2x+3x-3y+3y=-24-12; 5х=-36 x= y=
Ответ: (-7,2;3,2)
|
-решение задач с помощью систем уравнений (учебник алгебры: №1103,1109)
Пример №1103
Дано:
Пусть основание равнобедренного треугольника x, тогда боковая сторона y.
Решение:
; ;
;
Ответ: боковая сторона равна 12см.
8 класс ( Ю.Н.Макарычев и др.под ред. С.А.Теляковского)
-системы отсутствуют, как отдельный модуль для рассмотрения новых способов вычисления; вводится понятие квадратных уравнений и способы их решения, что необходимо при дальнейшей работе с системами уравнений
9 класс ( Ю.Н.Макарычев и др.под ред. С.А.Теляковского)
Системы уравнений второй степени:
способ подстановки
способ сложения
способ введения новой переменной
- по сложности
| | способ подстановки
|
| | способ подстановки
|
| | способ подстановки
|
| способ сложения
| |
| | способ сложения
|
| | способ сложения способ подстановки |
|
| способ введения новой переменной
|
- Также присутствует решение некоторых задач с помощью систем уравнений (№460,472,476)
Пример №460. Дано:
Пусть один катет треугольника x, тогда второй y.
Решение:
; ; ; ;
Решая квадратное уравнение, получаем корни 35 и 12.
Ответ: боковая сторона равна 35см и 12 см.
Можно рассмотреть более подробно следующую задачу:
Разность катетов прямоугольного треугольника равна 23 см, а его гипотенуза равна 37 см. Найдите площадь треугольника.
Решение.
Первый этап. Составление математической модели.
Обозначим длину одного катета xсм, а другого ycм.
Тогда x−y=23 — разность катетов прямоугольного треугольника.
Применив теорему Пифагора, получим второе уравнение:
x2+y2=372
x2+y2=1369
Составляем систему двух уравнений с двумя неизвестными:
Второй этап. Работа с составленной моделью.
Решим данную систему:
Способом подстановки получим: y1=12
y2=-35 не подходит по смыслу задачи,
найдем х из первого уравнения системы: х=35
Третий этап. Ответ на вопрос задачи.
Найдём площадь прямоугольного треугольника.
S=xy=
⋅12⋅35=210см2
Ответ: площадь равна 210 см2
5. Диагностика знаний учащихся 9 классов
Проведем проверочные работы в 9 классах, посмотрим динамику выполнения.
Задания:
1 вариант:
Решить уравнение: 2x+7=4
Упростить выражение: 2x+3y-2(x-2y)
Решить уравнение: 2x2+6x-8=0
Решить систему уравнений способом подстановки:
Решить систему уравнений способом сложения:
2 вариант:
Решить уравнение: 2x+7=4
Упростить выражение: 2x+3y-2(x-2y)
Решить уравнение: 2x2+6x-8=0
Решить систему уравнений способом подстановки:
Решить систему уравнений способом сложения:
Получили следующие результаты:
| Решаемость заданий | № задания |
|
|
|
|
|
|
| |||||||||||
| 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
| ||||||||
| верно | 81,00% | 63,00% | 76,50% | 63,00% | 67,50% |
|
|
|
|
|
|
| |||||||
| неверно | 19,00% | 37,00% | 19,00% | 28,00% | 28,00% |
|
|
|
|
|
|
| |||||||
| нет ответа | 0,00% | 0,00% | 4,50% | 9,00% | 4,50% |
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
6. Вывод:
Нами было осуществлено исследование по теме: «Систематизация заданий по решению систем уравнений второй части ОГЭ, конструирование подготовительных упражнений», разработана цепочка вспомогательных заданий, проведена диагностика учебников по математике по данной теме, рассмотрена динамику выполнения заданий в 9 классах в результате мониторинга уровня осознанности знаний при решении текстовых задач.

 Получите свидетельство
Получите свидетельство Вход
Вход



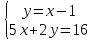
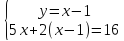 ;
;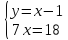 ;
;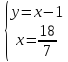 ;
;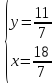 ;
;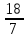 ;
;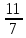 )=(
)=(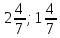 )
)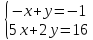 ;
;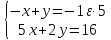 +
+








 «Систематизация заданий по решению систем уравнений второй части ОГЭ, конструирование подготовительных упражнений» (76.3 KB)
«Систематизация заданий по решению систем уравнений второй части ОГЭ, конструирование подготовительных упражнений» (76.3 KB)
 0
0 1137
1137 54
54 Нравится
0
Нравится
0


