
Автор:
Горина Лариса Владимировна,
учитель математики
МАОУ СШ №1
г. Михайловска

© Горина ЛВ
► КОНТРПРИМЕР — это пример, опровергающий верность некоторого утверждения...
► Построение КОНТПРИМЕРА — это обычный способ опровержения гипотез...
► Существует много утверждений, неверность которых очень легко доказывается с помощью КОНТПРИМЕРА...
► Бывает, что к одному и тому же заданию можно подобрать несколько КОНТРПРИМЕРОВ...
© Горина ЛВ
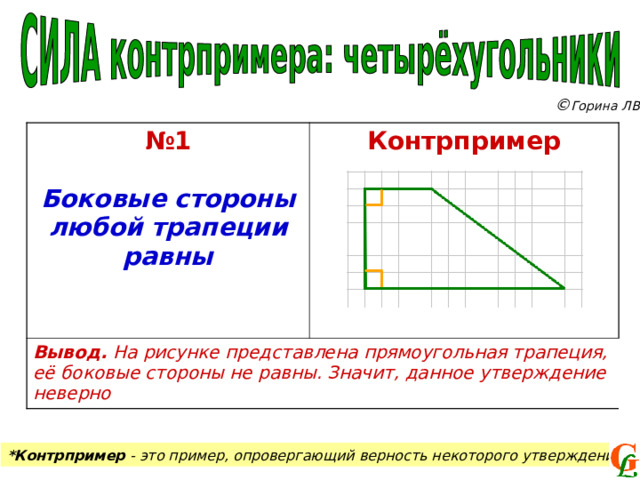
№ 1
Боковые стороны любой трапеции равны
Контрпример
Вывод. На рисунке представлена прямоугольная трапеция, её боковые стороны не равны. Значит, данное утверждение неверно
*Контрпример - это пример, опровергающий верность некоторого утверждения
© Горина ЛВ
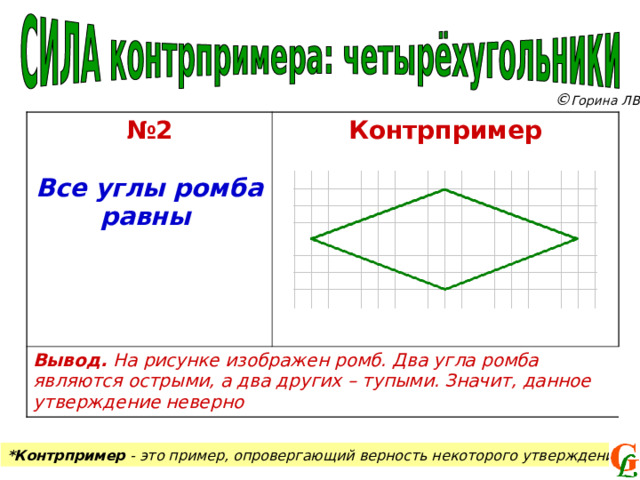
№ 2
Все углы ромба равны
Контрпример
Вывод. На рисунке изображен ромб. Два угла ромба являются острыми, а два других – тупыми. Значит, данное утверждение неверно
*Контрпример - это пример, опровергающий верность некоторого утверждения
© Горина ЛВ
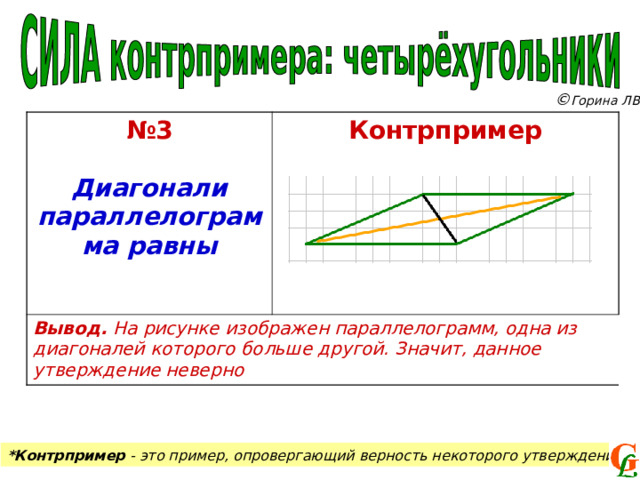
№ 3
Диагонали параллелограмма равны
Контрпример
Вывод. На рисунке изображен параллелограмм, одна из диагоналей которого больше другой. Значит, данное утверждение неверно
*Контрпример - это пример, опровергающий верность некоторого утверждения
© Горина ЛВ
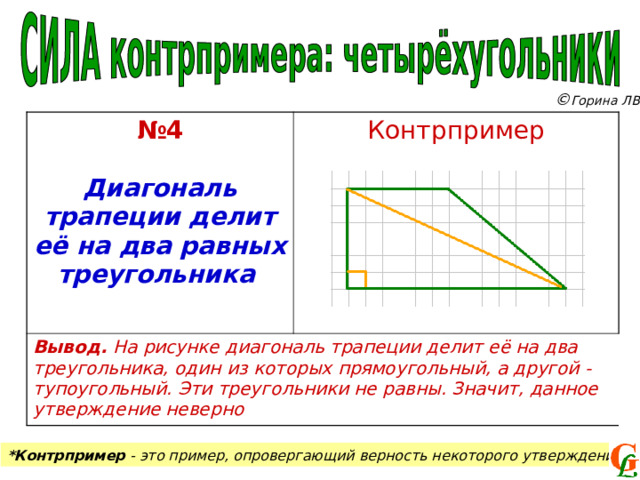
№ 4
Диагональ трапеции делит её на два равных треугольника
Контрпример
Вывод. На рисунке диагональ трапеции делит её на два треугольника, один из которых прямоугольный, а другой - тупоугольный. Эти треугольники не равны. Значит, данное утверждение неверно
*Контрпример - это пример, опровергающий верность некоторого утверждения
© Горина ЛВ
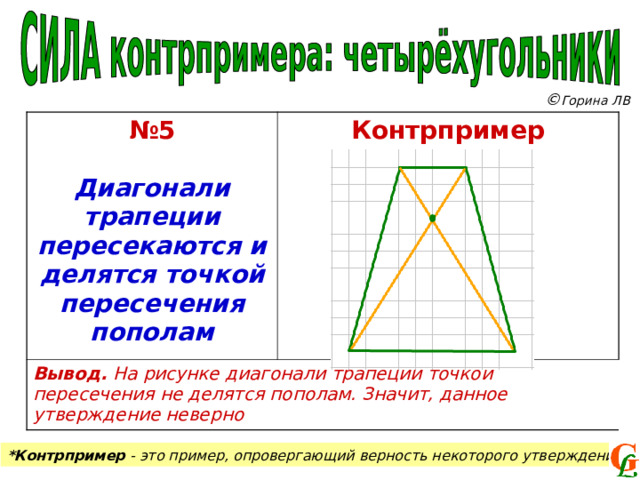
№ 5
Диагонали трапеции пересекаются и делятся точкой пересечения пополам
Контрпример
Вывод. На рисунке диагонали трапеции точкой пересечения не делятся пополам. Значит, данное утверждение неверно
*Контрпример - это пример, опровергающий верность некоторого утверждения
© Горина ЛВ
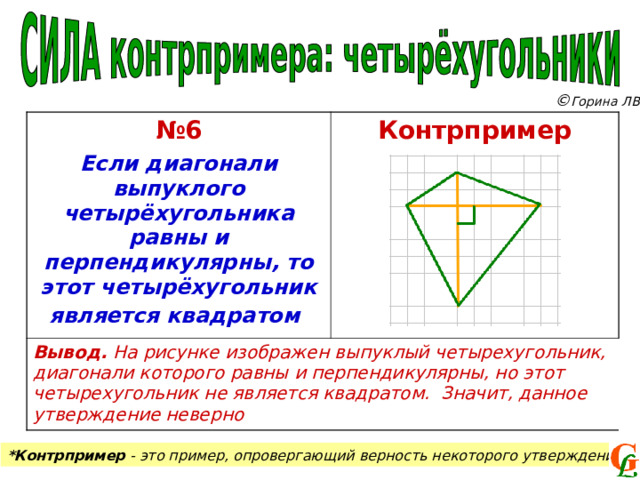
№ 6
Если диагонали выпуклого четырёхугольника равны и перпендикулярны, то этот четырёхугольник является квадратом
Контрпример
Вывод. На рисунке изображен выпуклый четырехугольник, диагонали которого равны и перпендикулярны, но этот четырехугольник не является квадратом. Значит, данное утверждение неверно
*Контрпример - это пример, опровергающий верность некоторого утверждения
© Горина ЛВ
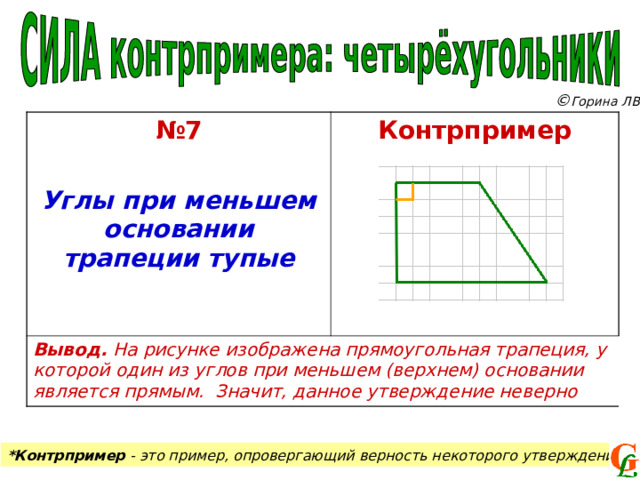
№ 7
Углы при меньшем основании трапеции тупые
Контрпример
Вывод. На рисунке изображена прямоугольная трапеция, у которой один из углов при меньшем (верхнем) основании является прямым. Значит, данное утверждение неверно
*Контрпример - это пример, опровергающий верность некоторого утверждения

 Получите свидетельство
Получите свидетельство Вход
Вход












 Сила контпримера: ЧЕТЫРЁХУГОЛЬНИКИ (145 KB)
Сила контпримера: ЧЕТЫРЁХУГОЛЬНИКИ (145 KB)
 0
0 1240
1240 19
19 Нравится
0
Нравится
0


