Теоретическая часть
СИСТЕМЫ СЧИСЛЕНИЯ
Наиболее точной моделью числа является его запись. Запись числа возникла давно и связана с важнейшей практической потребностью – запоминанием числа. Действительно, после того как число записано, набор камешков, палочек и прочих используемых для счета предметов освобождается для работы с другими числами.
На протяжении тысячелетий формы записей чисел претерпевали большие изменения. Сначала многие народы имели свои отдельные системы записи чисел. До настоящего времени дошли лишь некоторые из них.
Существуют различные формы представления одного и того же числа, различные системы записи числа.
Системой счисления называется способ записи с помощью выделенного набора специальных знаков (цифр, букв).
Разновидности систем счисления с примерами
Греческая
Римская
Древнеегипетская
Вавилонская
Система счисления майя
Г реческая система счисления – это метод представления числа с помощью букв греческого алфавита и некоторых знаков доклассического периода. Другие названия данного способа – ионийская, новогреческая.
реческая система счисления – это метод представления числа с помощью букв греческого алфавита и некоторых знаков доклассического периода. Другие названия данного способа – ионийская, новогреческая.
В Греции рассматриваемый алфавитный способ записи чисел стал применяться в III веке до н.э. Буквы греческого алфавита соответствуют следующим числам:
С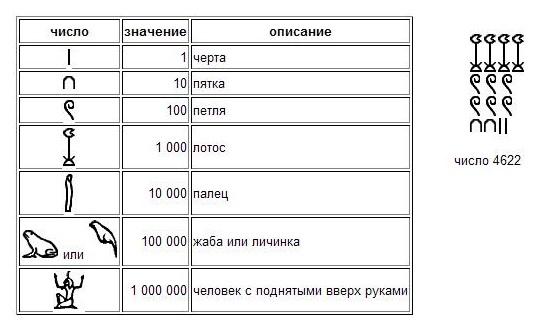 помощью ионийской системы можно записать лишь числа от 1 до 999.
помощью ионийской системы можно записать лишь числа от 1 до 999.
Способ записи чисел, используемый в Древнем Египте, основывался на иероглифах. С помощью этих символов записывались основные числа 1, 10, 100 и т.д. Другие числовые значения получались с помощью сложения ключевых чисел.
 Вавилонская (первая система счисления, частично основанная на позиционном принципе)
Вавилонская (первая система счисления, частично основанная на позиционном принципе)
Вавилонская система счисления – использует для обозначения чисел знаки в виде вертикальных и горизонтальных насечек – клиньев. Такую систему написания знаков называют клинописью.
Вавилонскую систему записи числовых значений называют также шестидесятеричной. Принцип разделения числового пространства на группы по 60 единиц используется и в настоящее время для определения временных отрезков. Один час состоит из 60 минут, одна минута – из 60 секунд.
В качестве примера возьмем число 32:
![]()
Число 60 и все его степени так же обозначаются прямым клином, что и “1”. Поэтому вавилонская система счисления получила название шестидесятеричной.
Все числа от 1 до 59 вавилоняне записывали в десятичной непозиционной системе, а большие значения — в позиционной с основанием 60. Число 92:

Ц ифры майя – это запись чисел с основанием 20, используемая племенами майя.
ифры майя – это запись чисел с основанием 20, используемая племенами майя.
Для обозначения чисел в различных бытовых ситуациях Майя использовали непозиционную систему представления чисел, в которой записывались числа от 0 до 19 с помощью знаков, представляющих собой комбинации точек и горизонтально расположенных отрезков. Ноль имел обозначение пустой ракушки. Цифры составлялись из точки и горизонтальной черточки. Точка означала единицу, черта – пятерку.
Задания
Задание 1. Запишите числа в десятичной системе счисления. Укажите название системы счисления
|
| Десятичная | Название непозиционной системы счисления |
| | 23 | вавилонская |
| | 31 | вавилонская |
|
| 13 | майя |
|
| 17 | майя |
Задание 2. Запишите числа в вавилонской системе счисления
| Десятичная | Вавилонская |
| 32 | |
| 11 | |
Задание 3. Запишите числа в системе счисления майя
| Десятичная | Майя |
| 15 |
|
| 7 |
|
Все существующие системы счисления можно разделить на два типа:
Позиционные
Непозиционные
Непозиционные системы счисления
В непозиционной системе счисления цифры не изменяют своего значения при изменении их расположения
Римская система счисления.
Для записи чисел в ней используется 7 специальных обозначений:
I – единица,
V – пять, C – сто,
X – десять, D – пятьсот,
L – пятьдесят, M – тысяча, которые называют римскими цифрами.
При записи чисел пользуются определенными правилами:
Написанные друг за другом одинаковые цифры обозначают их сумму, например, II – два;
Если меньшая цифра стоит перед большей, то из большей вычитается меньшая, например IV – четыре; При этом, левая цифра может быть меньше правой максимум на один порядок: так, перед L(50) и С(100) из «младших» может стоять только X(10), перед D(500) и M(1000) — только C(100), перед V(5) — только I(1); число 444 в рассматриваемой системе счисления будет записано в виде CDXLIV = (D-C)+(L-X)+(V-I) = 400+40+4=444.
Если после, то цифры складываются, например XI – одиннадцать.
Римскую систему счисления называют еще и аддитивной, (additio – сложение), т.к. число образуется сложением значений отдельных цифр. Например, XII = X+I+I
Например,
XXI=X+X+I = 21
XIX=X+X+(-I) = 19
LXI=L+X+I = 61
MMXIX=2019
CXXI=121
LXVII=67
95= =VC (C-V=100-5)
105= CV (C+V=100+5)
32 =XXXII
1986=MCMLXXX
2024=MMXXIV
Позиционные системы счисления
Более привычна для нас десятичная система счисления. Она является позиционной системой счисления.
В позиционной системе счисления значение каждой цифры числа зависит от того, в каком месте (позиции, разряде) она записана.
В десятичной системе счисления значение каждой цифры определяется ее местом в записанном числе.
Например: в записи числа 222 цифра 2 повторяется трижды, при этом цифра 2, стоящая слева, означает количество сотен, стоящая в центре – количество десятков и справа – количество единиц.
Теперь мы можем сформулировать отличие позиционных систем счисления от непозиционных и их преимущества над непозиционными системами.
Отличия
В непозиционных системах счисления значение цифры НЕ ЗАВИСИТ от ее положения в записи числа.
Например: у числа ХХХ (тридцать) цифра Х в любом месте означает число десять.
В позиционных системах счисления значение каждой цифры ИЗМЕНЯЕТСЯ С ИЗМЕНЕНИЕМ ее ПОЗИЦИИ (положения) в последовательности цифр, изображающих число.
Например: у числа 321 цифра 3 означает 300, цифра 2 - 20, а цифра 1 – 1. Преимущества позиционных систем
Выполнение арифметических операций производится достаточно легко (даже над очень большими числами).
Например: выполните следующие операции LXVII +CCXXI,
67+221
У чисел, записанных в позиционной системе счисления, более краткая запись.
Итак, позиционная система счисления – это система счисления, в которой значение цифр определяется их местом (позицией) в записанном числе.
Позиции цифр в записи числа называют его разрядами.
Например: для записи числа 12 надо в младший разряд записать 2, а в более старший – 1. при этом цифра 1 будет означать количество десятков, а цифра 2 – единиц.
Количество (р) различных символов, используемых для изображения числа в позиционной системе счисления, называется основанием системы счисления.
В десятичной системе счисления р=10 и для записи любого числа используется 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Древнее изображение десятичных цифр (рис.) не случайно: каждая цифра обозначает число по количеству углов в ней. Например, 0 - углов нет, 1 - один угол, 2 - два угла и т.д. Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.

КАКИЕ ЕЩЕ СУЩЕСТВУЮТ ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ?
В компьютере наиболее удобной и надежной оказалась двоичная система счисления.
Двоичная система счисления:
р=2, используемые цифры - 0, 1
Восьмеричная система счисления:
р=8, используемые цифры - 0, 1, 2, 3, 4, 5, 6, 7
Шестнадцатеричная система счисления:
р=16, используемые цифры - 0, 1, 2, 3, 4, 5, 6, 7, 8,9 и буквы A, B, C, D, E, F, заменяющие числа - 10,11,12,13,14,15
Набор символов, используемый для обозначения цифр, называется алфавитом.
Задания:
Перечислите алфавит пятеричной системы счисления и определите основание этой системы счисления – 0-4, р=5
Перечислите алфавит семеричной системы счисления и определите основание этой системы счисления – 0-6, р=7
Любое число N, в позиционной системе можно представить в следующем виде:
N=an*рn + an-1*рn-1 + … + a0*р0 + a-1*р-1 + … + a-m*р-m, (2)
где р – основание системы
n+1 – количество разрядов в целой части числа
m – количество разрядов в дробной части числа
Например:
Определить основание системы, количество разрядов целой и дробной частей
2466,67510 – р=10, n=3, m=3
1011,112 – р=2, n=3, m=2
48110 (р=10, n=2, m=0) 4*102+8*101+1*100
10 (р=10, n=1, m=0) 22*101+7*100
2305,54810 (р=10, n=3, m=3) 2*103+3*102+5*100+5*10-1+4*10-2 +8*10-3
10110,1012 (р=2, n=4, m=3) 1*24+0*23+1*22+1*21+0*20+1*2-1+0*2-2 +1*2-3
32,18 (р=8, n=1, m=1) 3*81+2*80+1*8-1
Задание
Задание 1.
Запишите числа в десятичной системе счисления
CLX _________________________ MCIX ________________MMCCLV____________
⮜⮟⮟ ________________________ ⮟⮟⮟ ____________________________





•••__________________________ • • ____________________________
Запишите числа в римской системе счисления
23 ____________________________ 816 ________________93___________
Запишите числа в вавилонской системе счисления
41 ____________________________ 16 _______________________________
Запишите числа в системе счисления майя
4 ____________________________ 18 _______________________________
Задание 2. Разложить число по формуле, указать основание систем (р), количество разрядов целой части (n+1) и дробной части (m)
65,259410
111011,1011002
423,45
Перевод чисел из различных систем счисления
Перевод чисел из недесятичной позиционной системы счисления
в десятичную
Чтобы перевести число из недесятичной системы сложения в десятичную необходимо разложить число по формуле N=an*рn + an-1*рn-1 + … + a0*р0 + a-1*р-1 + … + a-m*р-m, а затем найти сумму:
Например, перевести число 10110,101 из двоичной системы в десятичную
10110,1012 = 1*24 + 0*23 + 1*22 + 1*21 + 0*20 + 1*2-1 + 0*2-2 + + 1*2-3 = 16+0+4+2+0+0,5+0+0,125 =22,62510
5D8,AC116 = 5*162 + 13*161 + 8*160 + 10*16-1 + 12*16-2 + + 1*16-3 = 1280 + 208 + 8 + 0,625 + 0,047 + 0,006 = 1496,67810
256,547=2*72+5*71+6*70+5*7-1+4*7-2=98+35+6+0,7+0,08=139,7810
Перевод числа из десятичной системы счисления
в другую позиционную систему
Представим десятичное число в общем виде N,M, где N — целая часть числа, а М — его дробная часть. Для перевода десятичного числа в позиционную систему счисления с основанием р необходимо воспользоваться двумя правилами: одно определяет технологию перевода целой части числа, а другое — дробной части.
Правило перевода целой части числа состоит из следующих этапов:
♦ число N делится на новое основание р;
♦ полученный остаток запоминается или записывается (это будет цифра младшего разряда);
♦ целая часть полученного частного снова делится на р;
♦ опять записываем полученный остаток (это будет цифра следующего разряда) и т. д.
Такое последовательное деление продолжается до тех пор, пока целая часть частного не окажется меньше, чем основание системы счисления р. Эта последняя целая часть частного будет цифрой старшего разряда. Результат формируется путем последовательной записи слева направо цифры старшего разряда и всех записанных остатков в порядке, обратном их получению.
Правило перевода дробной части числа состоит из следующих этапов:
♦ дробная часть числа умножается на основание р;
♦ запоминается или записывается цифра результата, переносимая в целую часть;
♦ оставшаяся дробная часть числа умножается на основание р;
♦ снова фиксируется цифра результата, переносимая в целую часть, и т. д.
Такое последовательное умножение продолжается до тех пор, пока в дробной части не будет получен ноль или достигнута требуемая точность, например 5 знаков после запятой. Результат формируется в виде последовательной записи зафиксированных цифр переносов в целую часть в том порядке, в котором они были получены.
Пример перевода из десятичной системы счисления в двоичную

Задания.
Прочитайте шуточное стихотворение А. Н. Старикова «Необыкновенная девочка» и попробуйте разгадать загадку поэта. Для этого выпишите упомянутые в стихотворении числа и переведите их в десятичную систему счисления.
| Ей было тысяча сто (12) лет, | Она ловила каждый звук |
| Когда, пыля десятком (2) ног, | И десять темно-синих глаз
|
Переведите числа в десятичную систему счисления
11023=1*33+1*32+0*31+2*30=27+9+2=3810
61,118=6*81+1*80+1*8-1+1*8-2=48+1+0.125=49.12510
Переведите десятичные числа в двоичную.
7,25
383,31
7.25=111,01
7:2=3(1)
3:2=1(1)
0,25*2=0,5(0)
0,5*2=1 (1)
383,31=111100101,01001
383:2=242(1)
242:2=121(0)
121:2=60(1)
60:2=30(0)
30:2=15(0)
15:2=7(1)
7:2=3(1)
3:2=1(1)
0,31*2=0,62(0)
0,62*2=1,24(1)
0,24*2=0,48(0)
0,48*2=0,96(0)
0,96*2=1,92(1)
Сравните числа 158510 и 1152,25
1152:5=230(2)
230:5=46(0)
46:5=9(1)
9:5=1(4)
1152=14102
0,2*5=1,0(1)
0,2=0,1
158510 14102,110
Перевод двоичных чисел в восьмеричную систему счисления
Если для перевода десятичного числа в восьмеричное и наоборот вы пользовались известным вам правилом, то для перевода двоичного числа в восьмеричное и наоборот правило иное:
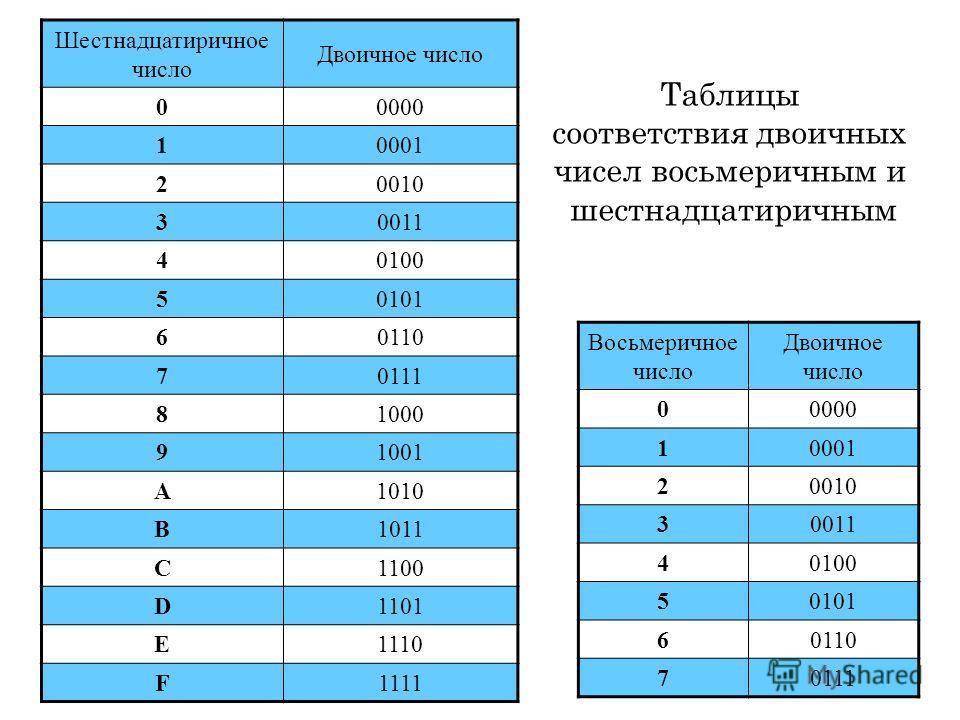
Для перевода любого двоичного числа в восьмеричное необходимо разделить число на триады и перевести каждую из них отдельно (в недостающие триады дописываются нули). Направление деления на триады для целой части – справа налево, для дробной – слева направо от точки. Для этого пользуются таблицей. (таблица в конце лекции)


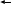 Например: записать двоичные числа 1010000102 и 11,0011112 в восьмеричном виде
Например: записать двоичные числа 1010000102 и 11,0011112 в восьмеричном виде
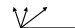 101 000 0102 = 5028 011 , 001 1112 = 3,178
101 000 0102 = 5028 011 , 001 1112 = 3,178
3, 1 7
Двоичные триады
Максимальное число, использующееся при записи в восьмеричной системе счисления, 7 (1112). Числа большие 7 будут иметь 4 разряда и больше, поэтому деление (условное) производится на тирады (т.е. 3 разряда рассматриваются вместе)
Пользуйтесь при переводе таблицей.
Для перевода восьмеричного числа в двоичное необходимо записать каждую цифру в виде двоичной триады.
Например: записать число 3158 в двоичном виде
3 = 0112
 1 = 0012 3 1 58 3158 = 110011012
1 = 0012 3 1 58 3158 = 110011012
5 = 1012 011 001 101
Задания
Преобразовать двоичные числа в восьмеричные
1010100112=5238
101100,11012=54,648
1101110011,00111112=1563,1748
Преобразовать восьмеричные числа в двоичные
7228=1110100102
6247,2138=110010100111,0100010112
52,4718=101010,100110012
Шестнадцатеричная система счисления – позиционная система счисления с основанием, равным 16.
Каждый разряд в шестнадцатеричной системе счисления может принимать значения от 0 до 15. Для изображения чисел используются десятичные цифры от 0 до 9 и буквы латинского алфавита A, B, C, D, E, F, которым ставятся в соответствие 10, 11, 12, 13, 14, 15. Эта замена вызвана необходимостью использовать одноразрядные символы.
Перевод двоичных чисел в шестнадцатиричную систему счисления
Для перевода любого двоичного числа в шестнадцатеричное необходимо разделить полученный результат на тетрады и перевести каждую из них отдельно (в недостающие тетрады записываются нули).
Например: записать двоичные числа 1010000102 и 11,0011112 в шестнадцатеричном виде
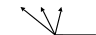 1 0100 00102 = 14216 11 , 00 11112 = 3,0F16
1 0100 00102 = 14216 11 , 00 11112 = 3,0F16
3 , 0 F
Двоичные тетрады
Для перевода шестнадцатеричного числа в двоичное необходимо записать каждую. Цифру в виде двоичной тетрады.
Например: записать число 30D16 в двоичном виде
3 = 112
 0 = 02 3 0 13 30D16 = 11000011012
0 = 02 3 0 13 30D16 = 11000011012
D = 13 = 11012 0011 0000 1101
Задания
Преобразовать двоичные числа в шестнадцатеричную
1110100102=1D216
110010100111,0100010112=CA7,4516
101010,100110012=2A,9916
Преобразовать шестнадцатеричные числа в двоичные
63016=011000110002
9213,4216=1001001000010011,010000102
52,А7С16=01010010,1010011111002
Практическая часть
Практическая работа №1
Системы счисления. Позиционные и непозиционные системы счисления.
Задание 1. Переведите числа из римской системы счисления в десятичную:
MCMXCIX
MDCCXCIX
CDXXXVII
MCCXII
Задание 2. Запишите десятичное число в римской системе счисления:
145, 2020, 86
Задание 3. Запишите пример в десятичной системе, вычислите ответ и запишите его в римской системе:
MCM – XC=
CDXLIV+CCCXXXIII=
DCCCLXXXVIII-DCLXVI=
Задание 5. Запишите основание и алфавиты следующих позиционных систем
| Система счисления | Алфавит | Основание |
| Десятичная |
| Р= |
| Восьмеричная |
| Р= |
Задание 6. Алфавиты каких позиционных систем счисления приведены ниже? Запишите их название.
| Алфавит | Система счисления |
| 0, 1, 2 |
|
| 0, 1, 2, 3, 4, 5, 6 |
|
Задание 7. Запишите наименьшее основание системы счисления, в которой могут быть записаны следующие числа:
| Числа | Система счисления |
| 9, 122, 1100, 14 |
|
Задание 8. Разложите указанное число, укажите основание системы (р), количество разрядов целой части (n-1) и дробной части (m).
869
1001,12
52,3768
12002,023
Практическая работа №2
Перевод чисел из одной системы счисления в другую
Задание №1. Перевести числа в десятичную систему счисления, указать основание системы, количество разрядов целой и дробной части.
5637
1102,2103
АС3,916
1011001,11012
Задание №2. Перевести числа из десятичной системы счисления (до 5 знаков после запятой)
143 в двоичную систему счисления
672,1 в восьмеричную систему счисления
934 в шестнадцатеричную систему счисления
486,21 в пятеричную систему счисления
62,03 в троичную систему счисления
Задание №3. Перевести числа из двоичной системы счисления в восьмеричную.
11001110002
10111100,1100111012
110110001,100100112
Задание №4. Перевести числа из восьмеричной системы счисления в двоичную.
275,2368
5642,018
Задание №5. Перевести числа из двоичной системы счисления в шестнадцатеричную
10001010002
1110001,10110012
101111010,1100101112
Задание №6. Перевести числа из шестнадцатеричной системы счисления в двоичную.
384,С516
F102,D16
Задание 7. Определите минимальное основание для чисел и поставьте числа в порядке возрастания.
10012,021 50,46 49,5
Итоговое занятие по теме «Системы счисления»
Системы счисления принципиально делятся на ...
Позиционные и непозиционные
Алфавитные и цифровые
Римские и арабские
Однозначные и многозначные
В позиционных системах счисления значение цифры ...
Не зависит от ее позиции в записи числа
Является постоянным в записи числа
Зависит от ее позиции в записи числа
Постоянно и всегда равно 10
Какой числовой эквивалент (значение) имеет цифра 6 в числе 7561?
1000
100
10
1
Основание системы счисления определяется как ...
Количество цифр, используемых для записи чисел
Количество цифр, не используемых для записи чисел
Цифры, чаще других используемые при записи чисел
Количество арифметических операций, выполняемых над числами
В семеричной системе счисления используется алфавит: ...
1, 2, 3, 4, 5, 6, 7
0, 1, 2, 3, 4, 5, 6, 7
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
0, 1, 2, 3, 4, 5, 6
Какое минимальное основание имеет система счисления, если в ней записаны числа 127, 222, 115?
4
2
7
8
Какое наибольшее число можно записать четырьмя цифрами в троичной системе счисления?
1111
2222
3333
4444
Если в записи чисел могут быть использованы только цифры 0 1 2 3, то такая система счисления называется …
Двоичной
Семеричной
Троичная
Четверичной
К какой системе счисления относится число II?
Вавилонской
Римской
Системе майя
Древнегреческой
Какому числу в десятичной системе счисления соответствует число MXCII?
1102
1112
192
1092
Задание 2.
Определите систему счисления и запишите числа в десятичной системе счисления
XXIX LXXXIII


••_ • •
Запишите числа в римской системе счисления
99 705
Запишите числа в вавилонской системе счисления
58 36
Запишите числа в системе счисления майя
9 15
Задание 3. Выполнить следующие преобразования
Переведите числа в десятичную систему счисления, укажите основание системы, количество разрядов целой и дробной части.
110012 428,35
Переведите числа из десятичной системы счисления (до 5 знаков после запятой):
в троичную 2122,1
в двоичную 58,2
Переведите числа из двоичной системы счисления в восьмеричную и шестнадцатеричную.
10110101012 111000100,1011012
Переведите числа из шестнадцатеричной системы счисления в двоичную
25А16 FA45,27116
23

 Получите свидетельство
Получите свидетельство Вход
Вход












 Сборник учебных материалов "Системы счисления" (459.41 KB)
Сборник учебных материалов "Системы счисления" (459.41 KB)
 0
0 372
372 10
10 Нравится
0
Нравится
0




