Введение
«Ведь жить – это значит решать задачи!»
Л.М.Фридман
Актуальность работы.
Текстовые задачи являются важным средством обучения математике. С их помощью мы знакомимся и получаем опыт работы с величинами, узнаем взаимосвязи между ними. Использование арифметических способов решения задач развивает смекалку и сообразительность, умение ставить вопросы, отвечать на них.
Посмотрев художественный фильм «Чебурашка», я решила создать несколько задач разных типов и предложить ребятам из своего класса решить эти задачи.
Цель: Составить сборник текстовых математических задач по содержанию художественного фильма «Чебурашка»
Задачи:
1) Просмотреть фильм «Чебурашка»
2) Изучить типы текстовых задач;
3) Составить сборник задач
4) Решить задачи и выполнить оценку полученных результатов.
Предметом проекта является изучение типов текстовых задач, процесс составления текстовых задач по содержанию фильма «Чебурашка».
Структура работы включает в себя: введение, основную часть и заключение.
Понятие задачи в математике.
Математика проникает почти во все области деятельности человека, что положительно сказалось на темпе роста научно-технического прогресса. В школьном курсе математике, особое внимание уделяется текстовым задачам.
Изучение текстовых задач происходит в начальной и основной школе, но рассматриваются они недостаточно глубоко, таким образом, приобретённые в основной школе навыки и знания решения текстовых задач со временем теряются. Исходя из этого, чтобы верно решить любые текстовые задачи, нам необходимо рассмотреть классификации этих задач.
Определим прежде всего, что подразумевается под задачей.
Задача — это текст, содержащий численные компоненты. Структура этого текста такова, что в нем можно выделить условие и требование (которое не всегда выражено в форме вопросительного предложения).
Решить задачу — значит выполнить арифметические действия, определенные условием, и удовлетворить требованию задачи.
При решении каждой задачи мы производим небольшое математическое исследование, с помощью которого проверяется наша сообразительность и способность к логическому мышлению.
Текстовые задачи мы можем условно классифицировать по типам:
задачи на числовые зависимости;
задачи, связанные с понятием процента;
задачи на «движение»;
задачи на «концентрацию смесей и сплавов»;
задачи на «работу» и т. д.
По методу решения:
арифметический метод
алгебраический метод
геометрический метод.
Решение текстовых задач делится на несколько этапов:
| Название этапа РЗ | Цель этапа | Приемы выполнения этапа |
| 1)Анализ задачи | Основное назначение этого этапа понять в целом ситуацию, описанную в задаче, выделить условия и требования, назвать известные и искомые объекты, выделить все отношения (зависимости) между ними. | -Чтение задачи -Перефразировка задачи -Толкование слов -Задаём специальные вопросы -Вспомогательная модель (краткая запись, таблица, чертёж, схема, рисунок). |
| 2)Поиск плана решения | Установить связь между данными и искомыми объектами, наметить последовательность действий. | -Разбор задачи: 1. От данных к вопросу 2. От вопроса к данным
|
| 3)Осуществление плана решения | Найти ответ на требования задачи, выполнить все действия в соответствии с планом. | -Запись по действиям с пояснением, без пояснений. -Запись в виде выражения. |
| 4)Проверка решения задачи. | Установить правильность или ошибочность выполненного решения. | -Установление соответствия между результатом и условием. -Решение другим способом. -Составление и решение обратной задачи. |
Иногда при решении сложных задач трудно с самого начала определить количество вводимых неизвестных. Выбирая неизвестные, мы создаём математическую модель ситуации, описанной в условии задачи. Поэтому все соотношения должны из конкретных условий задачи, т. е. необходимо каждое условие представить в виде уравнения или записать иным образов в виде математической модели.
Методы решения текстовых задач.
Существуют различные методы решения текстовых задач:
арифметический,
алгебраический,
геометрический,
логический,
практический и др.
В основе каждого метода лежат различные виды математических моделей.
Дадим краткую характеристику первых трех методов решения текстовых задач, которые наиболее часто встречаются в школьном курсе математики.
Арифметический метод.
Решить задачу арифметическим методом – значит найти ответ на требование задачи посредством выполнения арифметических действий над числами. Одну и ту же задачу во многих случаях можно решить различными арифметическими способами. Задача считается решенной различными способами, если её решения отличаются связями между данными и искомыми, положенными в основу решений, или последовательностью использования этих связей.
Алгебраический метод.
В науке данный метод трактуется как метод буквенных вычислений. Решить задачу алгебраическим методом – это значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений (или неравенств). Одну и ту же задачу можно также решить различными алгебраическими способами. Задача считается решенной различными способами, если для её решения составлены различные уравнения или системы уравнений (неравенств), в основе составления которых лежат различные соотношения между данными и искомыми.
Геометрический метод.
Он состоит в том, что логическое доказательство или решение задачи направляется наглядным представлением, иногда доказательство или решение видно из наглядной картины. Под геометрическим методом решения алгебраических задач будем понимать в дальнейшем метод решения, заключающийся в использовании геометрических представлений (изображений), законов геометрии и элементов аналитических методов (уравнений (неравенств)).
Как составить математическую задачу.
Изучив рекомендованную литературу, я составила памятку для составления задачи Памятка учащимся:
1) Сбор фактических данных.
2) Процесс составления задачи.
Из источника надо выбрать математическое содержание и тип задачи. Задача должна решаться средствами арифметики или с помощью уравнения и относиться к одной из следующих тем:
– Действия с натуральными числами.
– Единицы измерения длины, площади.
– Действия с дробями с одинаковыми и разными знаменателями.
– Нахождение части числа и числа по его части.
- Нахождение части, которую одно число составляет от другого.
3) Формулировка условия задачи.
Надо, чтобы задача была интересной, понятной и звучала корректно с точки зрения математики.
Как работать над формулировкой задачи:
а) выписать из источника все числовые данные и установить зависимости между числами или выяснить, во сколько раз (на сколько) одно число отличается от другого;
б) составить условие задачи в виде схемы, сформулировать условие и вопрос задачи;
в) решить задачу выбранным методом или получить ответ, выполнив следующие действия…
4) Правильное оформление задачи.
Требования:
– корректность формулировки условия;
– наличие подробного решения;
1. На завтрак Чебурашка съел 24 апельсина, что составляет 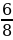 от того, что он съел на обед. Сколько апельсинов съел Чебурашка на завтрак и обед вместе?
от того, что он съел на обед. Сколько апельсинов съел Чебурашка на завтрак и обед вместе?

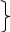 На завтрак - 24 а. -
На завтрак - 24 а. - 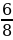 от
от
? а.
1) 24:6*8=32 (а.)- съел на обед
2) 24+32=56(а.)-съел всего
Ответ: 56 апельсинов съел Чебурашка всего.
2. Продавщица мороженого в первый день продала 32 мороженого, что составляет 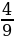 от того сколько она продала во второй день. На сколько больше она продала во второй день, чем в первый.
от того сколько она продала во второй день. На сколько больше она продала во второй день, чем в первый.
на ? 

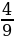 от
от
Во второй день- ?
1) 32:4*9+72(шт.) - во второй день
2) 72-32=40(шт.) - продала больше чем в первый день
Ответ: на 40 штук мороженого продала во второй день больше, чем в первый.
3. В 1 магазине на витрине стоит 8 тортов, что составляет 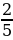 от того количества тортов, что стоит на витрине во втором магазине. Сколько тортов стоит на витрине в третьем магазине, если во всех трех магазинах всего 36 тортов.
от того количества тортов, что стоит на витрине во втором магазине. Сколько тортов стоит на витрине в третьем магазине, если во всех трех магазинах всего 36 тортов.

 В 1-ом магазине - 8шт. -
В 1-ом магазине - 8шт. - 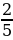 от
от
Во 2-ом магазине - ? 36 шт.
В 3-ем магазине - ?
1) 8:2*5=20(шт.) - во втором
2) 20+8 = 28 (шт.) - в первом и во втором
3) 36-28=8(шт.) -в третьем магазине
Ответ: 8 тортов стоит в третьем магазине на витрине.
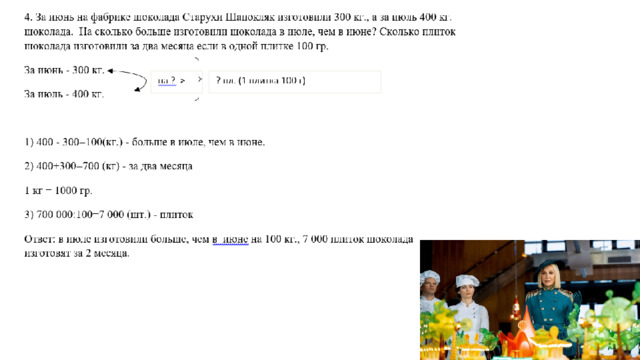
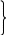 4. За июнь на фабрике шоколада Старухи Шапокляк изготовили 300 кг., а за июль 400 кг. шоколада. На сколько больше изготовили шоколада в июле, чем в июне? Сколько плиток шоколада изготовили за два месяца если в одной плитке 100 гр.
4. За июнь на фабрике шоколада Старухи Шапокляк изготовили 300 кг., а за июль 400 кг. шоколада. На сколько больше изготовили шоколада в июле, чем в июне? Сколько плиток шоколада изготовили за два месяца если в одной плитке 100 гр.
? пл. (1 плитка 100 г) на ? 


За июль - 400 кг.
1) 400 - 300=100(кг.) - больше в июле, чем в июне.
2) 400+300=700 (кг) - за два месяца
1 кг = 1000 гр.
3) 700 000:100=7 000 (шт.) - плиток
Ответ: в июле изготовили больше, чем в июне на 100 кг., 7 000 плиток шоколада изготовят за 2 месяца.
5. Скорость мотоцикла Гены 10 км/ч. Он доехал от дома до фонтана за 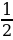 ч. Это расстояние составляет
ч. Это расстояние составляет 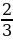 расстояния от фонтана до пекарни. Какое расстояние от дома до пекарни?
расстояния от фонтана до пекарни. Какое расстояние от дома до пекарни?
|
| V | t | S |
| от дома до фонтана | 10 км/ч | |
|
| от фонтана до пекарни | 10 км/ч |
| ? км |
| от дома до пекарни | 10 км/ч |
| ? км |
S=V*t
1) 10*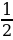 = 5 (км) - расстояние от дома до фонтана
= 5 (км) - расстояние от дома до фонтана
2) 5:2*3=7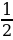 (км) - расстояние от фонтана до пекарни
(км) - расстояние от фонтана до пекарни
3) 5+7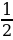 = 12
= 12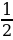 (км)
(км)
Ответ: 12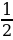 км от дома до пекарни.
км от дома до пекарни.
 6. Повар приготовил для Чебурашки 50 блюд (горячее, десерты и салаты). Из них 12 десертов, что составляет
6. Повар приготовил для Чебурашки 50 блюд (горячее, десерты и салаты). Из них 12 десертов, что составляет 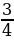 от всех горячих блюд. Сколько салатов приготовил повар?
от всех горячих блюд. Сколько салатов приготовил повар?
50 б.

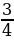 от
от
Горячие блюда - ? б.
Салаты - ? б.
1) 12:3*4=16 (б.) - горячих блюд
2) 16+12=28 (б.) - горячих блюд и десертов
3) 50-28=22 (б.) - салатов
Ответ: 22 салата приготовил повар для Чебурашки.
Вывод.
Математика - вечное живое дерево науки. С древнейших времён известно, что математика учит правильно и последовательно мыслить, логически рассуждать.
Цель и задачи поставленные перед началом работы, были выполнены. Благодаря этому проекту, я узнала много нового о математических задачах, научилась составлять текстовые задачи, порекомендую своим одноклассникам решить составленные мной задачи.
Муниципальное автономное общеобразовательное учреждение
« ГИМНАЗИЯ № 7 «СИБИРСКАЯ»

ПРОЕКТ
Математические задачи в художественном фильме «Чебурашка»
выполнила: ученица 5 «В» класса
МАОУ«Гимназия №7 «Сибирская»
Белявская Дарья
руководитель: учитель математики
Тарабановская Елена Петровна
г. Новосибирск, 2023г.
Список литературы:
Научно-теоретический методический журнал «Математика в школе», №3-2001. – 80с.
. Научно-теоретический методический журнал «Математика в школе», №2-2005. – 80с.
Л.Ф. Пичурин «За страницами учебника алгебры», С.- 35
Универсальная школьная энциклопедия. Т.З.Биографии/Глав. Ред. Е.Хлебалина; вед. ред. Д.Володихин. – М.: Аванта+, 2003. – 592 с.: ил.
Журнал «Математика» №17 – 1998.- 18с.
Журнал «Математика» №9 – 1998.- 18с.
https://www.google.com/url?sa=i&url=https%3A%2F%2Frbclife.ru%2Fnews%2F63bd2dce9a794716f9540336&psig=AOvVaw1K2bwftk3dOB7olBmvzh4g&ust=1678465298485000&source=images&cd=vfe&ved=0CAMQjB1qFwoTCJia0Zaiz_0CFQAAAAAdAAAAABAD
https://www.google.com/url?sa=i&url=https%3A%2F%2Fwww.youtube.com%2Fwatch%3Fv%3Dx1qvJL7NF9s&psig=AOvVaw1K2bwftk3dOB7olBmvzh4g&ust=1678465298485000&source=images&cd=vfe&ved=0CAMQjB1qFwoTCJia0Zaiz_0CFQAAAAAdAAAAABAI

 Получите свидетельство
Получите свидетельство Вход
Вход


 ? км
? км

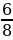 от того, что он съел на обед. Сколько апельсинов съел Чебурашка на завтрак и обед вместе?
от того, что он съел на обед. Сколько апельсинов съел Чебурашка на завтрак и обед вместе? 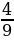 от того сколько она продала во второй день. На сколько больше она продала во второй день, чем в первый.
от того сколько она продала во второй день. На сколько больше она продала во второй день, чем в первый.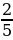 от того количества тортов, что стоит на витрине во втором магазине. Сколько тортов стоит на витрине в третьем магазине, если во всех трех магазинах всего 36 тортов.
от того количества тортов, что стоит на витрине во втором магазине. Сколько тортов стоит на витрине в третьем магазине, если во всех трех магазинах всего 36 тортов.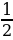 ч. Это расстояние составляет
ч. Это расстояние составляет 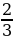 расстояния от фонтана до пекарни. Какое расстояние от дома до пекарни?
расстояния от фонтана до пекарни. Какое расстояние от дома до пекарни?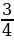 от всех горячих блюд. Сколько салатов приготовил повар?
от всех горячих блюд. Сколько салатов приготовил повар?





















 Самостоятельная работа (5.28 MB)
Самостоятельная работа (5.28 MB)
 0
0 874
874 33
33 Нравится
0
Нравится
0




