Сабақтың тақырыбы: Азайту амалы

Сабақтың тақырыбы: Азайту амалы

Азайту амалын анықтау үшін , бастауыш сыныптарда шығарылатын мынадай есепті талдайық.

Есеп: Айданада 10 дәптер бар.Оның 6-ы торкөз, қалғаны кең жол дәптерлер.Айданада неше кең жол дәптер бар?

Есеп сұрағына жауап беру үшін 10-нан 6-ны шегереміз. 10-6=4 . Бұл есеп неліктен азайту амалымен шығарылды?Айданадағы дәптерлерді шартты түрде дөңгелектермен белгілейік.Сонда біз іс жүзінде 10 элементі бар жиынның бір бөлігін айырып алдық.Ендеше, азайту амалы жиындарды айыру амалына негізделеді.

6

4

10

Анықтама: Теріс емес бүтін а және b сандарының айырымы деп а =n(A), b=n(B) және B 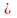A болатындай А және В жиындары айырымының элементтерінің санын айтады:

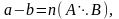мұндағы а =n(A), b=n(B) , B 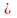A

Берілген анықтаманы пайдаланып, 10-6=4 екенін көрсетейік.

Мысалы:

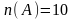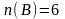
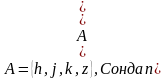, және B 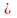A болатындай , басқа да А және В жиындарын алуға болар еді.Өйткені a-b айырымы

а =n(A), b=n(B) және B 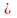A шартын қанағаттандыратын жиындарды таңдап алуға тәуелді емес.Теріс емес бүтін екі санның айырымы әрқашан бар ма? Деген сұрақ туындайды. B 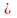A болғандықтан , 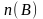болады. Ендеше, a-b айырымы болу үшін b

a-b айырымының мәнін табу амалын азайту деп атайды.

Азайтудың компонентері:

a-b=c, мұндағы а- азайғыш, b- азайтқыш, a-b өрнегі - айырма, ал c-айырманың мәні.

Анықтама: Теріс емес бүтін а және b сандарының айырымы деп, b санымен қосындысы а-ға тең болатын теріс емес бүтін с санын айтамыз:

Қосу мен азайту амалдары бір біріне кері амалдар деген түсінік бар.Азайтудың қосу арқылы берілетін анықтамасына сүйене отырып, келесі теоремаларды дәлелдейік.

Теорема: Теріс емес бүтін а және b сандарының айырмасы b

Дәлелдеуі: егер a=b болса,онда a-b=0.Ендеше a-b айырмасы бар.Егер b0 болса, онда b b

Сұрақтар:

1. Теріс емес бүтін а және b сандарының айырымы қалай анықталады?

2. Айырманың мәнінің жалғыз екендігі туралы теореманы дәлелде

3. Белгісіз қосылғышты табу ережесін тұжырымда

Үй жұмысы:

1. 12-8=4 және 24-6=18 өрнектері бойынша есептер құрастыр.

2. Назеркеде 9 дәптер бар еді.Ол оның 4 –еуін Арайға берді.Назеркеде неше дәптер қалды? Есеп неліктен азайту амалымен шығарылатынын түсіндіріп жаз.