ПЛАН Вступ І.Роль логічного мислення в процесі навчання 1.1. Поняття про мислення 1.2. Логічна структура питання ІІ. Методика розвитку логічного мислення в процесі навчання
Розвиток логічного мислення –необхідний аспект сучасного процесу навчання
Розвиток логічного мислення на уроках математики
2.2.1.Умови сприяння розвитку логічного мислення в
процесі вивчення математики
2.2.2. Логічні форми думок
2.3.Поняття,як логічна форма мислення
2.3.1.Логічна структура поняття
2.3.2.Поділ і класифікація понять
2.3.3.Запобігання можливим логічним помилкам при означенні понять
2.4.Основні методологічні прийоми формування понять
2.5.Судження, як форма логічного мислення
ВИСНОВОК
Вступ Протягом усього свідомого життя людина здобуває нові знання. Знання – це сукупність інформації, яку вона дістає з навколишнього світу в процесі практики. Пізнання є досить складним і багатогранним процесом.
Мислення – це вища форма пізнання світу. Свої думки людина виражає за допомогою мови. Навіть тоді, коли людина міркує “про себе”, вона неодмінно оформляє думки словами. Психологи називають це внутрішньою мовою.
Всебічні дослідження привели до висновку, що мислення і мова становлять нерозривну єдність. Якщо ж проаналізувати мову довільної групи людей, то можна помітити, що вона не однакова: одні люди виражають свої думки лаконічно, чітко, зрозуміло, обґрунтовано, інші – розпливчасто, не завжди зрозуміло. Про перших часто говорять, що вони мислять логічно, про других цього сказати не можна. Звичайно, кожний із нас хотів би мислити логічно. Але як цього досягти? Слово “ логічно” походить від терміна “логіка”. Логіка – це наука про форми і закони мислення. Хоч мислення має надзвичайно складну структуру, ще стародавні мислителі помітили, що значну частину умовиводів (висновків) ми робимо за стандартними схемами, незалежно від того конкретного матеріалу, яким оперуємо. Так, закон силогізму, яким ми часто користуємося, твердить: “ з істинності тверджень “A суть B” і “В суть С” випливає істинність твердження “ А суть С” незалежно від того, які об’єкти позначені буквами А, В, С.
Нажаль в шкільних навчальних програмах немає такого предмету як логіка, і тому дуже важливою стає проблема розвитку логічного мислення на уроках математики, фізики, літератури, історії тощо.
Мета даного дослідження - вивчити стан рішення проблеми розвитку логічного мислення в процесі навчання в учбово-методичній літературі. Розробити методичні рекомендації по розвитку логічного мислення в процесі навчання.
I. РОЛЬ ЛОГІЧНОГО МИСЛЕННЯ В ПРОЦЕСІ НАВЧАННЯ
1.1 ПОНЯТТЯ ПРО МИСЛЕННЯ
Сучасна практика поставила перед людством великі проблеми: збереження природи на нашій планеті, опанування новими істочниками енергії, освоєння всесвіту, ресурсів світового океану.
Всі науки виникли із практичних потреб людства: математика виникла із потреби виміру земельних ділянок і ємкості сосудів; астрономія – із потреб мореплавання; медицина – із потреб боротьби з хворобами. В процесі практичної діяльності людина, взаємодіючи з предметами і явищами об’єктивної дійсності, пізнає їх властивості, зв’язки, відношення. Пізнання здійснюється у двох основних формах: в формі різних почуттів і в формі абстрактного мислення. Процес пізнання починається з живого споглядання, з
відчуття. Відчуття дають знання про окремі сторони і властивості предметів: про колір, звук, твердість і т.п. На основі відчуттів виникає
сприйняття, воно відображає у свідомості людини предмет у цілому, без виділення його окремих властивостей. Знання які люди дістають у вигляді відчуття і сприйняття, залишаються у свідомості.
Уявлення – це чуттєво-наочний образ предметів, або явищ дійсності, що зберігаються у свідомості. Уявлення може бути результатом як безпосереднього, так і опосередкованого сприймання (наприклад, на основі почутого, прочитаного). Уявлення за своїм характером індивідуальне. Воно залежить від багатьох психічних особливостей людини, її минулого досвіду. Оскільки уявлення включає в себе елементи узагальнень, воно є вищою формою чуттєвого пізнання, тобто відображає навколишній світ глибше і диференційованіше, ніж відчуття або сприйняття. Уявлення — це перехідна форма між чуттєвим і абстрактним пізнанням, яке здійснюється за допомогою
мислення. Відчуття, сприйняття і уявлення дають безпосередні знання, тобто знання про ті ознаки предметів, які доступні органам чуттів. На цій стадії пізнання ще не відбувається відокремлення істотного від неістотного, необхідного від випадкового, окремого від загального. Метою ж пізнання людиною навколишнього світу є розкриття суті предметів і явищ та їх закономірностей. Цього людина досягає саме за допомогою абстрактного мислення. Знання, які здобуває людина на цій стадії пізнання за допомогою органів чуттів опосередковуються ними і знаходять своє відображення в логічних формах наших думок — поняттях, судженнях та умовиводах. Логіка мислення, закономірності, її зв'язки між думками обумовлені характером предметів і явищ об'єктивної дійсності, які відображаються, «копіюються», «фотографуються» мисленням.
Мислення має такі специфічні риси.
Воно є процесом опосередкованого відображення дійсності: логічні форми абстрактного мислення виникають на основі даних чуттєвого пізнання, завдяки якому мислення здійснює зв'язок із зовнішнім світом і відображає його. Аналізуючи чуттєві дані, думка людини проникає в суть предметів і явищ, розкриває їх закономірні зв'язки. Це дає можливість людській думці осягнути те, що не можна осягнути зором, слухом або дотиком. Наприклад, спостерігаючи за рухом окремих планет, людина зробила висновок про закони руху всіх космічних тіл.
Мислення – це процес узагальненого відображення світу, воно дає можливість виділити найістотніші загальні ознаки предметів.
Мислення має дійовий, активний і цілеспрямований характер.
Логічна структура питання
Питання грає особливу в процесі пізнання – все починається з питання, з постановки проблеми.
Видатний український педагог В.А. Сухомлинський значну роль в процесі навчання, розвитку логічного мислення учнів надавав вмінню вчителя ставити перед учнями запитання і добиватися правильних відповідей, які б сприяли інтелектуальному розвитку учня пробуджували власну думку підлітка.
Мислення учня напрямлене на пошуки відповідей на запитання. Викликати таку потребу в учня – сприяти розвитку логічного мислення.
Питання – це логічна форма, яка включає базисну інформацію і одночасно вказує на її недостатність з метою отримання нової інформації у вигляді відповіді.
Правила постановки простих і складних питань
- Коректність постановки питання: провокаційні, невизначені питання неприпустимі.
Передбачення альтернативності відповіді (“так” або “ні”) на уточнюючі питання.
Стислість і ясність питання: довгі заплутані питання ускладнюють їх розуміння.
Простота питання. якщо питання складне, то його краще розбити на декілька простих.
II. Методика розвитку логічного мислення в процесі навчання 2.1 Розвиток логічного мислення – необхідна умова сучасного процесу навчання
З необхідністю мислити, міркувати студенти зітхаються постійно. Виходячи із своєї життєвої практики вони поступово усвідомлюють, що правильно, а що неправильно. Виникає запитання: як навчитися не робити логічних помилок, тобто мислити правильно в усіх випадках, з будь-яких питань, відомих чи невідомих, про будь-які предмети, звичні для нас чи незвичні? Життєвий досвід, здоровий глузд у багатьох випадках допомагає уникати логічних помилок, проте не гарантує їх усунення. Кожна наука тією чи іншою мірою передбачає міркування. Навіть описові предмети, такі, як географія, біологія, анатомія, астрономія, не можуть обійтися без міркувань. Так, у географії потрібно не просто знати, який де клімат, яка рослинність, корисні копалини, а й уміти пояснити, чому, наприклад, в одному місці такий клімат, а в іншому — інший. Біологія при вивченні тварин і рослин не перелічує хаотично, без певної послідовності якісь факти, а викладає матеріал у строгому порядку, встановленому на основі певного міркування. Історія знайомить нас із подіями, умовами життя людей, їхніми звичаями, відмінними від тих, до яких ми звикли. Необхідність подумки переноситись в інші епохи, зіставляти їх між собою, знаходити подібність і відмінність - усе це, звичайно,
сприяє розвитку логічного мислення людини. Важливе значення для розвитку мислення людини має вивчення мови, як рідної, так і іноземної. Щоб правильно застосовувати граматичні правила, недостатньо вивчити їх, запам'ятати — тут потрібно вміти міркувати. Прагнення уникнути граматичних помилок зв'язується, таким чином, з необхідністю уникати логічних помилок. Ще більшою мірою сприяє розвитку мислення знання іноземних мов. Одна й та сама думка в різних монах виражається по-різному. Кожна мова містить дуже велику кількість різних елементів, які утворюють певну систему. Для передачі думок іноземною мовою треба вміти вибрати в цій системі саме ті елементи, які необхідні в даному випадку. Читаючи іноземний текст, потрібно в кожному випадку визначити, яку саме думку виражає дана комбінація мовних елементів, як літературно сформулювати її рідною мовою. Все це вимагає великих зусиль від мислення, особливо якщо система даної мови істотно відрізняється від системи рідної мови, якщо одна й та сама думка рідною і іноземною мовами виражається по-різному, так, що дослівно перекладена з іноземної мови фраза виглядає беззмістовною. В-таких випадках переклад іноземного тексту на рідну мову являє собою розв'язання свого роду логічних задач.
Значні можливості для розвитку логічного мислення відкриває вивчення літератури. Аналіз творів, вивчення психології і мови героїв, оцінка їх поведінки — усе це сприяє розвитку мислення. Дуже важливим е вміння писати твори. Успіх написання залежить не лише від знання фактичного матеріалу, а й від того, наскільки послідовно його автор зможе провести і довести основну думку свого твору, повно J чітко обґрунтувати кожний пункт складеного ним плану цього твору.
Для розвитку абстрактного мислення велику користь приносить вивчення природничих наук, наприклад хімії, в якій для дослідження причин різних явищ, вивчення атомів і молекул, недостатньо безпосереднього спостереження, і через це особливого значення набувають теоретичні міркування; фізики, де постійно виводяться одні положення з інших, що, природно, виробляє навички правильного мислення. Під час лабораторних робіт робляться висновки з фактів, одержаних у процесі дослідів. Хорошою практикою для розвитку логічного мислення є розв'язування фізичних задач.
Зауважимо, що розвиток логічного мислення залежить не лише від вивчення окремих наук, а й від методики їх вивчення, тобто не лише від того, що ми вчимо, а й від того, як саме. Якщо в основу покладено метод заучування окремих положень, то таке вивчення предмета розвиває мислення незначною мірою. Механічне заучування не лише окремих фактів, а й цілих міркувань аніскільки не змінює справи. Навіть математику можна вивчати так, що її вивчення не сприятиме розвитку мислення: якщо людина механічно запам'ятовує положення і цілі доведення (міркування), то при розв'язуванні задач замість того, щоб міркувати самостійно, вона просто повторює зазубрені приклади міркувань. Така методика вивчення предмета не тільки не розвиває, а й часто, навпаки, притуплює мислення. Коли людина розвиток свого мислення висуває на перший план, вивчення всіх наук може відіграти велику роль у розвитку навичок правильного мислення і цим самим зменшити кількість логічних помилок у міркуваннях.
Роль логічного мислення полягає в тому, що:
воно дисциплінує мислення, звільняє його від неясностей і плутанини;
навчаючи логічно мислити, ми тим самим підвищуємо загальну культуру мислення. Логічне мислення запобігає помилкам при розв’язуванні проблемних питань.
Логіка навчає методам відшукання нових результатів, свідомого використання понять, суджень, умовиводів.
2.2 РОЗВИТОК ЛОГІЧНОГО МИСЛЕННЯ НА УРОКАХ МАТЕМАТИКИ 2.2.1 Умови сприяння розвитку логічного мислення на уроках математики Наукою, яка найбільшою мірою сприяє розвитку логічного, вважають математику. Справді, тут на перший план висувається не стільки засвоєння окремих положень, скільки їх обґрунтування і доведення. Це стосується не лише геометрії, а й усіх інших розділів математики. Правда в курсі алгебри і початків аналізу велику роль відіграють обчислення, але перш ніж їх робити, необхідно виконати деякі перетворення, намітити план обчислень. Математика сприяє розвитку творчого мислення, змушуючи учнів шукати розв’язки нестандартних задач, розмірковувати над парадоксами, аналізувати зміст умов теорем і суті їх доведень . Виховний ефект уроків математики полягає у логічній строгості та стрункості умовиводів, які сприяють вихованню у студентів культури логічного мислення. Вивчаючи математику учні зітхаються з вимогами чітко і повноцінно аргументувати свої відповіді, припущення, пропозиції. На уроках математики учні оперують всіма формами мислення: поняттями судженнями, умовиводами. В процесі навчання на уроках математики виникають різні типи задач (стандартна, навчаюча, пошукова і проблемна). Основними компонентами задач є: умова, висновок, розв’язок, обґрунтування розв’язку; які можуть бути невідомі студенту у момент постановки даної задачі. Стандартна задача – це така задача, в якій чітко визначена умова, відомий спосіб розв’язку і його обґрунтування. Навчаючою є та задача, в якій один із вищезгаданих компонентів є невідомим. Якщо невідомими є два компоненти то задачу називають пошуковою, якщо три – проблемною. Цей розподіл задач є умовним, оскільки в залежності від рівня знань і методичної підготовки учня вона може бути віднесена до того чи іншого типу. Наприклад, при вивчені теми “Вписані чотирикутники” вчитель ставить перед учнями проблему: де треба розташувати автостанцію, щоб вона знаходилась на однаковій відстані від чотирьох сіл.
A
 B O D C
B O D C Учні старших класів в процесі навчання висувають різні гіпотези відмічають способи перевірки їх вірності самостійно “відкривають” закони, формули доказують теореми. Для розвитку логічного мислення важливо не тільки ставити проблемне питання, але й спонукати учнів до самостійної, творчої роботи, відкриття нових для них властивостей, закономірностей, а також давати логічне обґрунтування вірності всіх своїх міркувань, та вміти спростовувати хибні умовиводи.
2.2.2 ЛОГІЧНІ ФОРМИ ДУМОК
Отже, незалежно від конкретного змісту, всі висловлення мають однакові структурні елементи:
поняття про предмет
поняття про властивості предмета
елемент, що виражає відношення між цими поняттями.
Якщо поняття про предмет висловлення, умовно позначимо літерою S, а поняття про ознаки предмета — літерою Р І використаємо третій елемент, що виражає відношення між ними — слово «є» (або те є»), то зможемо записати загальну формулу для всіх наведених вище висловлень: «5 є Р» (або «S не є Р»). Символи S t Р називають при цьому логічними змінними, оскільки вони вживаються замість слів, які виражають різні поняття, а слова «є», «не є» — логічними сталими. Записана формула є символічним виразом однієї Із структур
Розглянемо два міркування:
1. Усі диференційовані функції е неперервними. Функція у=cosх диференційована. Отже, функція у=cos x - неперервна;
2. Усі многогранники є просторовими тілами. Тетраедр — многогранник. Отже, тетраедр є просторовим тілом.
Ці різні за змістом міркування мають такі спільні риси: 1) у кожному з них є по три висловлення, причому два перші обумовлюють третє; 2) у кожному міркуванні е спільне поняття, що міститься в перших двох висловленнях, зумовлюючи їх зв'язок, і не переходить у висновок (у першому міркуванні — це поняття «диференційована функція», у другому — «многогранник»; позначимо його літерою М) 3) в обох міркуваннях маємо и другому вихідному висловленні і у висновку поняття
«функція у=cosx», у другому — «тетраедр»; позначимо його через S).
У першому вихідному висловленні кожного міркування як і у висновку маємо також поняття про ознаку предмета думки (у першому міркуванні — це поняття «неперервна функція», у другому — «просторове тіло»; позначимо його літерою Р). Ці спільні особливості обох міркувань, які не залежать від їх конкретного змісту, і виражають структуру (форму) умовиводів, яка у даному випадку може бути записана таким чином: «Усі М є Р; S є М.. Отже, S є Р» (М, Р і S — логічні змінні). Проаналізувавши приклади Із судженнями і умовиводами, бачимо, що І в першому, і в другому випадках спільними для всіх висловлень будуть способи зв'язку між їх елементами. Отже, форма (структура) думки.— це її будова , спосіб поєднання її складових частин.
Основними логічними формами мислення є поняття, судження і умовивід. Поняття — це форма мислення, в якій відображається суть предметів і явищ реального світу в їх істотних, необхідних ознаках і відношеннях. Відображаючи істотні ознаки предметів, поняття дає можливість у думці відділити ці предмети від інших і кім сприяє глибшому їх пізнанню. Поняття несе в собі Інформацію про істотні і характерні ознаки одиничного предмета або певної множини предметів. У мові поняття фіксується словом або групою слів, Наприклад: «похідна», «границя», «місто Львів», «автор «Енеїди» і т.д.
Судження (висловлення) — це форма мислення, в якій стверджується або заперечується щось про предмет, про певні зв'язки між предметами І явищами. Матеріальною формою суджень є речення. Прикладами суджень є такі думки: «(sin х)' = cos x», «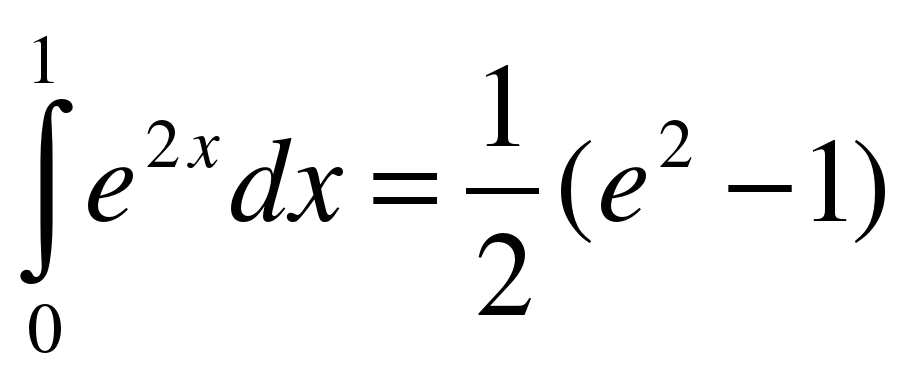 ,
,
«Усі прогресивні сили світу ведуть боротьбу за мир», «І. Я. Франко — автор повісті «Борислав сміється» та ін.
Умовивід — це виведення з вихідних суджень іншого судження, що несе в собі нову інформацію про предмет думки. У мові умовивід виражається послідовністю речень. Наприклад: «Якщо трикутник прямокутний, то для нього справедлива теорема Піфагора. Трикутник ABC — прямокутний. Отже, для трикутника ABC справедлива теорема Піфагора».
Логічні форми виникли в результаті практичної діяльності людини, її спостережень властивостей і відношень між предметами об'єктивної дійсності, тому зміст їх визначається змістом самих речей. «...Логічні форми і закони не пуста оболонка, а відображення об'єктивного світу». Логічні форми не залежать від змісту конкретних думок, а залежать від мислення в цілому і є відображеннями найпростіших і найзагальніших рис предметів. Об'єктивний характер змісту логічних форм робить їх загальнолюдськими, тобто єдиними для людей усіх рас, націй і класів.,
Як геометрія, абстрагуючись від конкретних фізичних властивостей тіл, вивчає геометричні форми, як граматика, абстрагуючись від конкретних значень слів І правил, вивчає граматичні форми, так само і формальна логіка, абстрагуючись від конкретного змісту думок, вивчає логічні форми мислення, тобто поняття, судження і умовиводи.
2.3 ПОНЯТТЯ ЯК ЛОГІЧНА ФОРМА МИСЛЕННЯ
2.3.1 Логічна структура поняття
Оволодіння будь-якою наукою немислиме без опанування системою понять цієї науки. Вище ми говорили, що поняття — це форма мислення, в якій відображається суть предметів і явищ реального світу в їх істотних, необхідних ознаках і відношеннях. Кожному поняттю відповідає певний об'єкт мислення. Ним може бути будь-який матеріальний предмет або явище природи чи суспільства, окремі властивості цих предметів чи явищ, окреме слово чи група слів і т. д.
Думаючи про якийсь конкретний предмет чи явище, ми одночасно думаємо про властивості цього предмета чи явища. Серед них є ряд властивостей, спільних з властивостями інших предметів, і ряд властивостей, якими предмет чи явище відрізняється від інших предметів чи явищ. Усе те, в чому предмети схожі один з одним або що їх відрізняє одне від одного, у логіці називається їх І знаками. Істотними вважаються ті ознаки предмета, кожна з яких необхідна, а їх сукупність достатня для того, щоб відрізнити даний предмет (чи клас предметів) під інших і дістати відповідь на запитання: «що це таке?». Наприклад, поняттям про квадрат буде поняття про прямокутник, у якого всі сторони рівні. Тут виділено дві ознаки: прямокутність і рівність усіх сторін. Кожна з цих двох ознак, взята окремо, відрізняє квадрат або від ромба, у якого всі сторони рівні, але немає характерної для квадрата властивості — прямокутності; або від нерівностороннього прямокутника. Виділені дві ознаки квадрата не тільки необхідні кожна зокрема; разом їх виявляється цілком достатньо для того, щоб за їх допомогою, не вказуючи ніяких інших ознак, ми могли відрізнити квадрат від будь-якої іншої фігури. Отже, виділені дві ознаки істотні для квадрата.
Залежно від мети, яку ставить перед собою людина, вона використовує ті або інші ознаки предмета, і тоді вони стосовно її практичних потреб стають істотними. Це означає, що істотність ознак предмета має відносний характер: одні й ті самі ознаки одного й того самого предмета є в одному випадку істотними, а в іншому — неістотними, Наприклад, для всіх людей вода має знамення як предмет, який задовольняє їхні певні життєві потреби і який відрізняється від молока, м'яса, заліза тощо. Водночас для біолога, фізика, хіміка з погляду їх науки істотні ознаки будуть різними. Біолога цікавитиме вода як певне середовище, в якому відбуваються життєві процеси організму. Тому для нього істотною ознакою води буде її здатність розчиняти певні тверді речовини, можливий рівень насиченості ЇЇ цими речовинами тощо. Для фізика істотними ознаками води будуть її властивості змінювати свій агрегатний стан і т. д. Хімічний склад води, атомарна будова її молекули будуть істотними ознаками для хіміка.
Існують родові і видові ознаки. Родовими називають ознаки, істотні для предметів одного класу. Наприклад, для ромба такою ознакою є належність до множини паралелограмів. Видовими називають такі ознаки, які лежать в основі певної групи предметів у межах роду. Наприклад, видовою ознакою ромба є рівність всіх його сторін, оскільки ця ознака виділяє ромби з множини усі паралелограмів.
2.3.2 Поділ і класифікація понять Поділ поняття — це логічна дія, яка полягає в мисленому поділі обсягу (роду) поняття на видові поняття, й яких відображені види предметів. Поділити обсяг поняття на його види можна лише за ознакою, яка є спільною для всіх предметів даного класу. Поняття, обсяг якого становить одиничний предмет, поділити не можна. Поняття, обсяг якого ділимо, називається діленим, а поняття, що утворюються в результаті поділу, називаються членами поділу. Ознака, за якою здійснюють поділ, називається основою поділу. Наприклад, дійсні числа ділять на раціональні і ірраціональні. Основа поділу — можливість для даного числа бути поданим у вигляді частки двох цілих чисел.
Щоб запобігти можливим помилкам при поділі обсягу поняття, в логіці розроблено такі правила:
Поділ понять має здійснюватися за однією основою. Якщо це правило порушено, то члени поділу нечітко визначають обсяг діленого поняття. Так, поділ трикутників на прямокутні, тупокутні і рівнобедрені неправильний, бо в основу поділу поняття «трикутник» покладено не одну , а дві ознаки, які далеко не тотожні: «наявність у трикутнику кута певної градусної міри» і «рівність
сторін трикутника». Поділ трикутників на тупокутні,
прямокутні і гострокутні є правильним.
Поділ повинен бути співмірним, тобто члени по
ділу в сумі повинні вичерпувати обсяг діленого поняття. У разі недодержання цього правила виникає помилка в поділі, яка має назву «надто вузького» або «надто широкого» поділу. Неповним, «надто вузьким» буде поділ поняття «трикутник», якщо ми дамо лише два види
трикутників — гострокутні і тупокутні, бо обсяг поняття «трикутник» не буде вичерпано (е ще прямокутні три
кутники).
Основою поділу поняття повинна бути чітко ви
значена істотна ознака. Якщо ж за основу поділу візьмемо випадкову або надуману ознаку, такий поділ приведе до помилок.
Члени поділу мають виключати один одного. Так,
поділ поняття «паралелограм» на види «прямокутник»,
с квадрат», «ромб» неправильний, бо названі члени по
ділу не виключають один одного, адже прямокутник може бути квадратом.
5. Поділ понять має бути послідовним, тобто ділене
повинне бути найближчим родом відносно членів поділу. Так, неправильним був би поділ дійсних чисел на цілі і дробові. Треба спочатку дійсні числа поділити на раціональні і ірраціональні, а потім раціональні числа поділити на цілі й дробові.
Частковим випадком поділу є так звана дихотомія .Дихотомія — це особливий вид поділу, коли поняття ділять на два суперечні поняття. Зміст одного з них заперечує зміст другого, а в сумі вони становлять рбсярі діленого поняття. Наприклад, поділ функцій на елементарні І неелементарні є дихотомією; тут маємо два члени поділу і дві множини, які в сумі становлять обсяг вихідного діленого поняття.
О собливим видом поділу є також класифікація. Тут не бмежуються поділом поняття на класи, а класи поділяють на підкласи, підкласи — на ще дрібніші частини і т. д. Наприклад, алгебраїчні вирази ми І
собливим видом поділу є також класифікація. Тут не бмежуються поділом поняття на класи, а класи поділяють на підкласи, підкласи — на ще дрібніші частини і т. д. Наприклад, алгебраїчні вирази ми І
поділяємо на раціональні і ірраціональні; раціональні вирази ділимо на цілі й дробові; цілі — на одночлени і многочлени. Схему класифікації алгебраїчних виразів можна зобразити як показано на малюнку
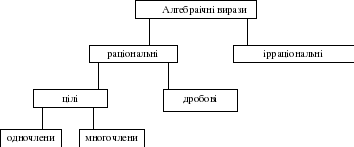
Основою такої класифікації є використання алгебраїчних операцій, за допомогою яких утворений вираз,!
Умовою цієї класифікації є перехід від родового поняття до найближчого в даному родовому понятті виду. Прикладом наукової класифікації може бути таблиця хімічних елементів Д. І. Менделєєва.
Логічний поділ (у тому числі класифікація) має велике значення при вивченні будь-якої науки бо розчленовуючи обсяг поняття на окремі класи чи види, що мають і подібні, і відмінні ознаки, ми маємо можливість глибше вивчати поняття конкретної науки і зв'язки між ними.
2.3.4 ЗАПОБІГАННЯ МОЖЛИВИМ ЛОГІЧНИМ ПОМИЛКАМ ПРИ ОЗНАЧЕННІ ПОНЯТЬ
Поняття вводять за допомогою логічної операції —означення. Особливо велику роль означення відіграють у математиці. Вони допомагають виділити даний предмет з множини інших об'єктів. Під означенням ми розуміємо таку логічну операцію, за допомогою якої розкривається зміст поняття. Отже, означити поняття — це перелічити всі істотні ознаки об'єктів, що входять у дане поняття. Словесне позначення поняття називається терміном. Наприклад, «кут», «коло», «переріз множин» — терміни. Поняття, яке означується, називають означуваним, a те поняття чи групу понять, за допомогою яких вводиться означуване поняття, називають означуючими поняттями. Наприклад: «Ромбом називається паралелограм, сторони якого рівні». У цьому означенні «паралелограм»— означуюче, а «ромб»—.означуване поняття.
У математиці існують різні види означень. Найпоширеніший з них — означення через найближчий рід і видову ознаку. Цей спосіб полягає в тому, що називаються, по-перше, найближчий рід, до якого належить означуване поняття, і, по-друге,— особлива ознака (або кілька таких ознак) даного поняття, що характеризує його як один з видів зазначеного роду. У курсі шкільної математики існують такі означення: «Центральним кутом у колі називається плоский кут з вершиною в центрі цього кола» (тут «плоский кут» — родове поняття, а властивість вершини плоского кута лежати в центрі кола — видова ознака); «Паралелограм — це чотирикутник, в якого протилежні сторони паралельні» (тут чотирикутник» — родове поняття, а властивість його протилежних сторін бути паралельними — видова ознака); «Якщо основою призми є паралелограм, то вона називається паралелепіпедом» (тут поняття «призма» — родове, а властивість призми мати в основі паралелограм — видова ознака) та ін.
2.4 ОСНОВНІ МЕТОДОЛОГІЧНІ ПРИЙОМИ ФОРМУВАННЯ ПОНЯТЬ
Щоб свідомо засвоїти те чи інше поняття, потрібно вміти з нескінченної кількості ознак відповідного предмета виділити ті, що визначають суть (зміст) предмета. Таке виділення ми здійснюємо за допомогою таких логічних прийомів, як порівняння, аналіз, синтез, абстрагування та узагальнення.
Порівняння — це логічний прийом» за допомогою якого встановлюється тотожність і відмінність ознак предметів і явищ дійсності. Порівнювати доцільно тільки ті предмети, які належать до однієї і тієї самої предметної області. Якщо ж предмети належать до різних предметних областей, не пов'язаних між собою, то вони не матимуть спільних ознак і порівняння їх позбавлене сенсу (не можна, наприклад, порівнювати трикутник і сніг або трактор і циліндр). Порівнювати треба найважливіші, істотні ознаки або такі, які хоч і не є істотними, але випливають з останніх або зумовлюють їх. Тільки за цієї умови можна проникнути в суть предметів, збагнути характерні особливості їх і на основі пізнання окремого розкрити загальне, істотне для цих предметів.
Аналіз (розклад, розчленування) — це мислене вичленення окремих властивостей предмета і дослідження їх як певних елементів цілого. Предмети об'єктивної дійсності постають перед людиною в усій своїй складності І таємничості. Щоб розкрити цю складність, людина повинна пізнати елементи, що утворюють ці предмети. Аналіз саме і є той метод, завдяки якому людина пізнає частини цілого, розчленовуючи це ціле на його складові елементи.
Синтез (з'єднання, складання, сполучення) — це мислене поєднання тих частин цілого, які вичленені й вивчені в процесі аналізу, встановлення взаємодії й взаємозв'язку їх та дослідження предмета як єдиного цілого. Синтез характеризується усвідомленим об'єднанням того, що розчленовано в аналізі. Аналіз і синтез у процесі мислення і утворення нових понять про предмети дійсності невіддільні один від одного, зумовлюючи й доповнюючи один одного. Це дві сторони одного і того самого процесу.
Абстрагування (відволікання) — це мислене відволікання від ряду неістотних властивостей і зв'язків досліджуваного предмета і виділення найістотніших і найхарактерніших його ознак, зв'язків і відношень з
метою проникнення в суть цього предмета. Абстракція е обов'язковим методом пізнання предметів дійсності: не можна утворити наукове поняття про предмет, не абстрагуючись від другорядних, неістотних його ознак.
Узагальнення є продовженням і одночасно завершенням логічної дії абстрагування. Це — поширення в думці загальних істотних ознак класу (множини) предметів виділених у процесі абстракції, на кожний предмет цієї множини. Внаслідок узагальнення людина усвідомлює загальне, що є характерним І най/типовішим для певної множини предметів. Так, у процесі пізнання особливостей окремих дерев — сосни, дуба, груші, сливи, вишні, кедра тощо — людина виділила в них найістотніше і найзагальніше (наявність стовбура, коріння, гілок) і подумки поширила ці ознаки на всю множину подібних до них предметів, сформувавши поняття «дерево».
Порівняння, аналіз, синтез, абстрагування та узагальнення взаємозв'язані між собою, їх використовує людина при формуванні будь-якого поняття. Згадаймо, як у нашій свідомості формувалось поняття паралельних прямих. Припустимо, що на дошці зображено пари прямих, що перетинаються, і пари прямих, які не мають спільних точок (мал. 13). При цьому пари прямих займають різне положення на площині: серед них є горизонтальні, вертикальні, похилі; у двох різних парах відстань між прямими, що не перетинаються, також різна. Прямі р і І (мал. 13, г) у полі дошки не перетинаються, але є впевненість, що вони перетнуться при продовженні. Спочатку ми порівнюємо між собою прямі, зображені на малюнку 13. Тоді виділяємо пари прямих, які мають істотні спільні ознаки: один клас пар прямих, що
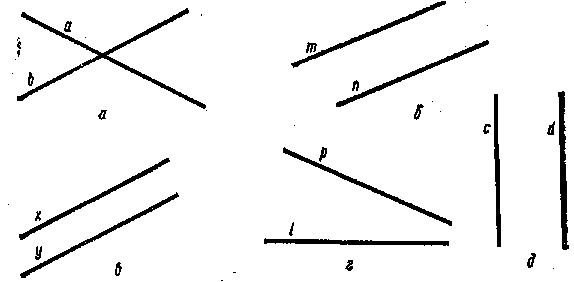
перетинаються, і другий клас, що не перетинаються. Виявляючи пари прямих, що не перетинаються, ми проводимо аналіз. Об'єднуючи ці пари в клас, виконуємо синтез. Називаючи загальну істотну ознаку (не перетинатися), ми не беремо до уваги неістотних ознак пар прямих (положення на площині, відстань між прямими ) — проводимо абстрагування. Узагальнення здійснюється тоді, коли вводиться термін «паралельні прямі на площині» і відповідний символ.
Рекомендовані вправи
1. В якому відношенні перебувають обсяги понять:
а) «квадрат», «трапеція»;
б) «трикутник», «коло»;
в) «трикутник», «прямокутний трикутник»;
г) «многогранник», «куб», «призма»;
д) «холодний», «гарячий»;
е) «далекий», «недалекий»;
є) «ромб», «трапеція», «квадрат». Покажіть відношення за допомогою кругів Ейлера.
2. Чи правильно здійснено поділ поданих нижче понять? Якщо неправильно» то визначте, яке правило порушене:
а) люди поділяються на чоловіків, жінок і дітей;
б) трикутники діляться на прямокутні, рівнобедрені і правильні;
в) прямі в просторі можуть перетинатися або бути паралельними;
г) війни поділяються на справедливі і несправедливі;
д) учнів нашого класу можна поділити на такі під
групи: ті, що вчаться лише на «5»; що вчаться на «4» і
«5»; що вчаться тільки на «З»;
е) функції поділяються на парні й непарні;
є) паралелограми поділяються на квадрати, прямокутники і ромби.
3. Здійсніть дихотомічний поділ понять:
а) «чотирикутник»; б) «многокутник»; в) «учень»; г) «функція».
4. Проаналізуйте означення. Якщо вони неправильні, встановіть, які правила в них порушені:
а) куля — це тіло, утворене обертанням кола навколо одного із своїх діаметрів;
б) паралелограм — це трапеція, в якій бічні сторони паралельні;
в) прямокутник — це ромб, в якого всі кути прямі;
г) коло — це крива замкнена лінія на площині;
д) функція у = f (х) називається парною, якщо І
е) піраміда називається правильною, якщо її основою є правильний многокутник;
є) круг — це частина площини, обмежена колом; а коло — це лінія, що обмежує круг, тобто границя круга.
2. 5 СУДЖЕННЯ, ЯК ФОРМА ЛОГІЧНОГО МИСЛЕННЯ
Окремими, ізольованими поняттями мислити неможливо. Найбільш
простою, елементарною формою логічного мислення є судження. У формі
судження знаходять свій вираз знання про взаємозв'язки предметів з їхніми
ознаками та взаємовідношення між ними. Як ми уже говорили, судження
(висловлення) — це форма мислення, в якій стверджується або
заперечується щось про предмет, про певні зв'язки і відношення між
предметами і явищами.
Кожна конкретна наука вивчає певне коло предметів і явищ дійсності, їх властивості і відношення, що становлять предметну область цієї науки. Слова «річ», «об'єкт», «предмет» е логічними синонімами, що позначають одне і те саме поняття. В логіці для позначення об'єкта дослідження найчастіше вживають слово «предмет». Тому надалі ми користуватимемося ним для позначення об'єкта мислення.
Судження як форма мислення істотно відрізняється від поняття. Це пов'язано з тим, що ці логічні форми по-різному відображають навколишню дійсність. Якщо поняття відображає сукупність істотних ознак предмета, то судження відображають окремі відношення між предметами і їх ознаками, причому шляхом ствердження чи заперечення. Судження, таким чином, надає людській думці закінчену форму, де може бути безпосередньо виражена істинність чи хибність нашого висловлення.
Перевіркою істинності змісту конкретного судження займається та наука, до предметної області якої належить предмет цього судження. Нагадаємо, що істина — це правильне, адекватне відображення предметів об'єктивної дійсності в думці людини. Так, істинним буде судження, в якому: а) зазначено ознаку, яка належить предмету (наприклад, «Коренями рівняння х2-5х+6 = 0 є числа 2 і 3»);
б) заперечується ознака, яка не належить предмету (наприклад, «Число 25671 не ділиться на 125»). Ці судження істинні, оскільки їх зміст відповідає дійсному стану речей. Істинність суджень ми піймається символом «і» («істина») або 1 («один»).
Хибним судження буде в тому разі, коли: а) за предметом стверджується ознака, яка не належить йому (наприклад, «Число 27383 ділиться на 3»); б) заперечується ознака предмета, яка належить йому (наприклад, прямокутний трикутник не містить прямого кута»).
Кожне судження має свою структуру (будову), яка залежить від того, що воно відображає — властивості чи підношення і взаємозв'язки між предметами. Судження, в яких стверджується (або заперечується) наявність властивості у того чи іншого предмета, називаються судженнями про належність, або атрибутивними судженнями. Наприклад, «Тетраедр — просторове тіло», «Число 8125 — непарне». Судження, в яких відображається підношення між двома і більше предметами, називаються судженнями про відношення, або релятивними судженнями. Наприклад, «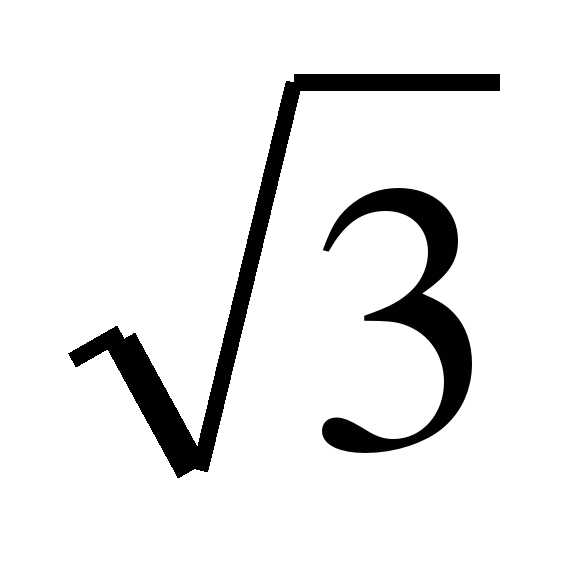 диться далі від початку координат, ніж точка
диться далі від початку координат, ніж точка
(-1;1)»тощо.
Проаналізуємо кілька атрибутивних суджень:
«Тетраедр є пірамідою»;
«Число 3 є коренем рівняння х2-х-6=0»;
«Жодне ірраціональне число не е цілим».
Кожне з них складається з трьох елементів: поняття
про предмет думки (відповідно «тетраедр», «число 3», «ірраціональне число»), поняття про властивості предмета думки (відповідно «піраміда», «корінь рівняння х2-х-6=0», «ціле число») І зв'язки («є», «не є»), що відображають відношення між предметом і його властивостями.
Поняття про ознаки (властивості) предмета називається предикатом судження і позначається літерою Р, зв'язка в судженні виражається словами «є», «не є», «суть», «не суть» і т.д. і є відображенням тих зв'язків, які існують між предметами і їх ознаками; інколи зв'язки в судженні випускається.
Треба чітко розмежовувати поняття «предмет судження» і «суб'єкт судження». Предмет судження — це предмет дійсності, про який йдеться в судженні, але який існує незалежно від мислення людини. Суб'єкт судження — це поняття про об'єктивно існуючий предмет, який став предметом судження. Ці два поняття пов'язані між собою, але вони нетотожні. Перший існує незалежно від другого, другий визначається першим. S (суб'єкт) і Р (предикат) називаються термінами судження. Нагадуємо, що S, Р — логічні змінні, а зв'язка — логічна стала.
На основі сказаного атрибутивні судження можна записати у вигляді формул «S є Р» або «S не є Р». Ці дві формули можна об'єднати в одну: «5 — Р», де риска означає зв'язку.
Розглянемо кілька суджень про відношення:
«Число 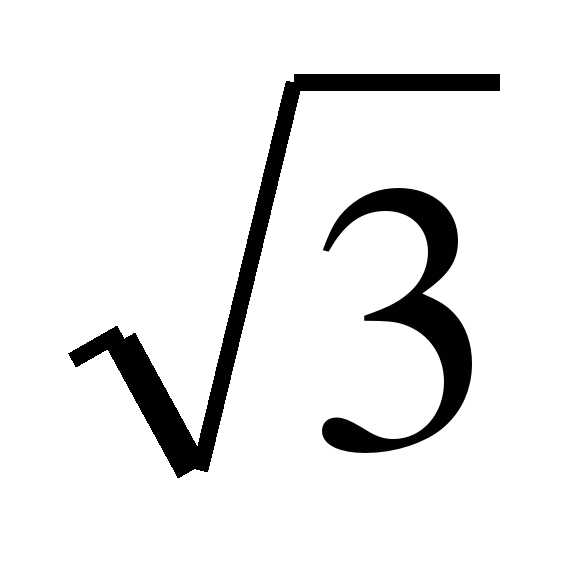 І/її знаходиться між числами 1 і 2»;
І/її знаходиться між числами 1 і 2»;
«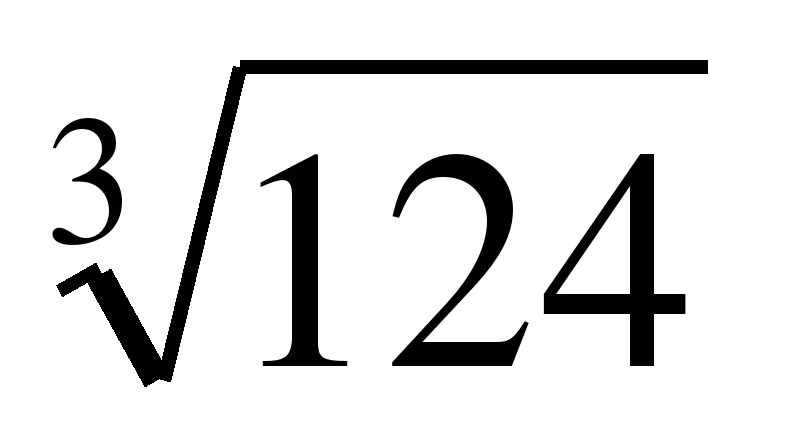
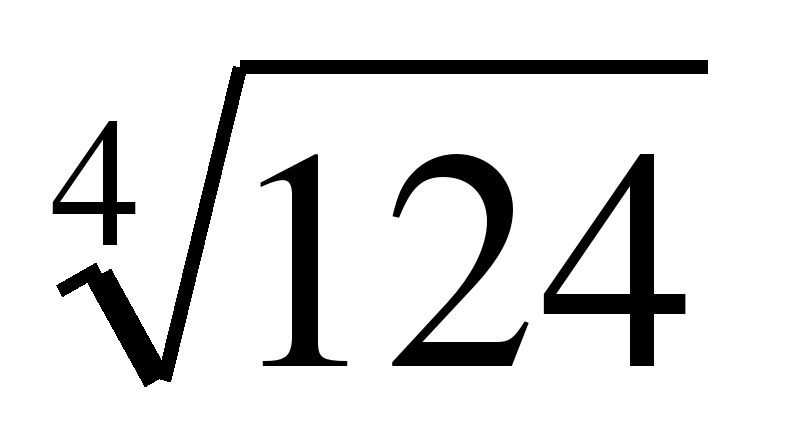 »;
»;
«Сума кутів опуклого n-кутника дорівнює 180°*(п — 2)».
Релятивні судження відображають найрізноманітніші відношення між предметами об'єктивної дійсності: рівності, тотожності, протилежності, суперечності, простору, часу, розміру, кількості, якості і т. д. Вони також мають суб'єктно-предикатну форму: в ролі предиката в них виступає відношення R, а в ролі суб'єкта — елементи предметної області. Таким чином, властивості і відношення, що відображаються в певних поняттях, виступають як предикати. Властивості притаманні окремим предметам (або множинам окремих предметів), тому їх називають одномісними предикатами. Відношення мають місце між двома, трьома і більше предметами (або множинами, що складаються з двох, трьох і т. д. предметів), тому їх називають багатомісними предикатами (двомісними — R (а, b), тримісними —R (a, b, с) і т. д.).
Зауважимо, що в релятивних судженнях порядок предметів, що відображаються суб'єктом, впливає на істинність суджень. Так, у судженні «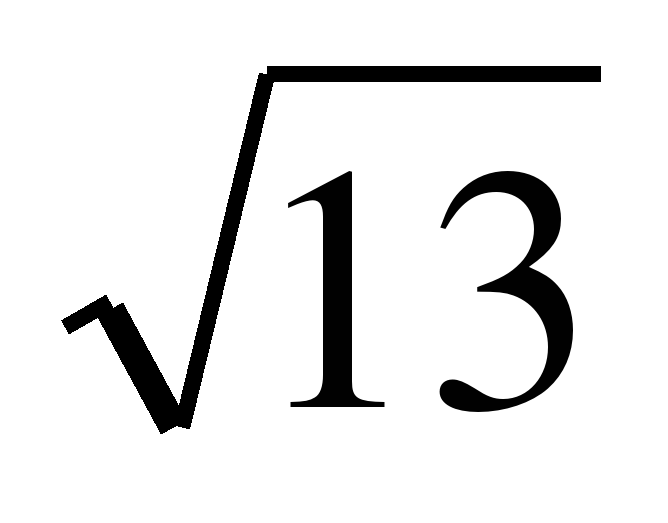
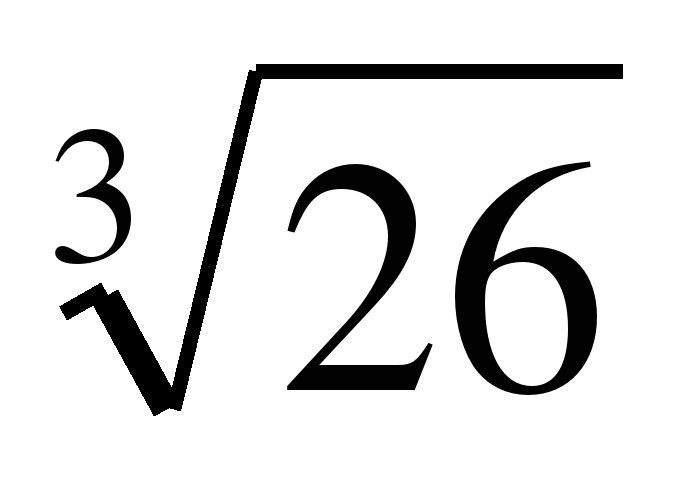 » відношення «більше», що з'єднує пару чисел у послідовності «
» відношення «більше», що з'єднує пару чисел у послідовності «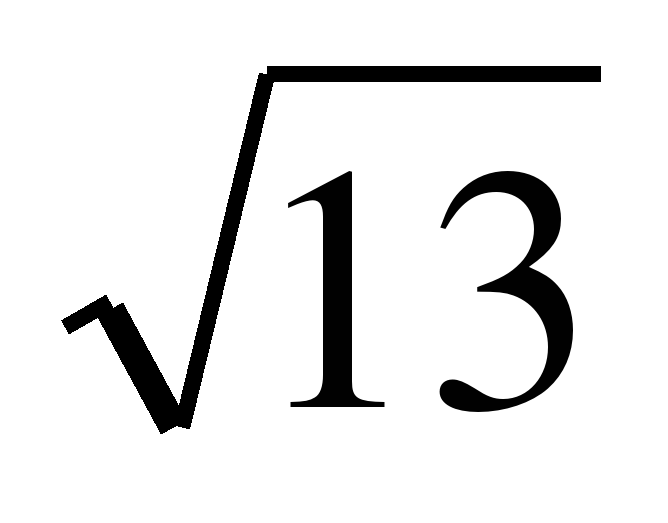 » «
» «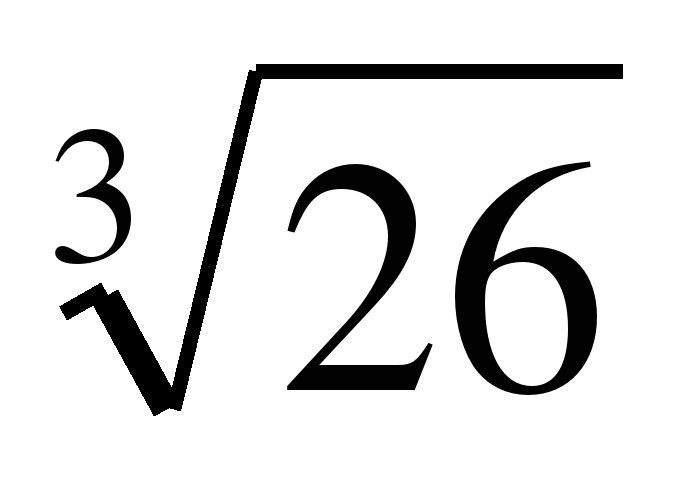 », дає можливість утворити істинне судження.
», дає можливість утворити істинне судження.
Судження в мові виражається за допомогою речення. Речення відносно судження є його своєрідною матеріальною оболонкою, а судження, як форма відображення об'єктивної дійсності, наповнює речення певним конкретним змістом. Тому якщо ми не можемо виразити якесь судження в реченні, то можна вважати, що в нас іще не сформувалось нове судження.
Граматичною формою судження е розповідне речення “об’єм кулі дорівнює 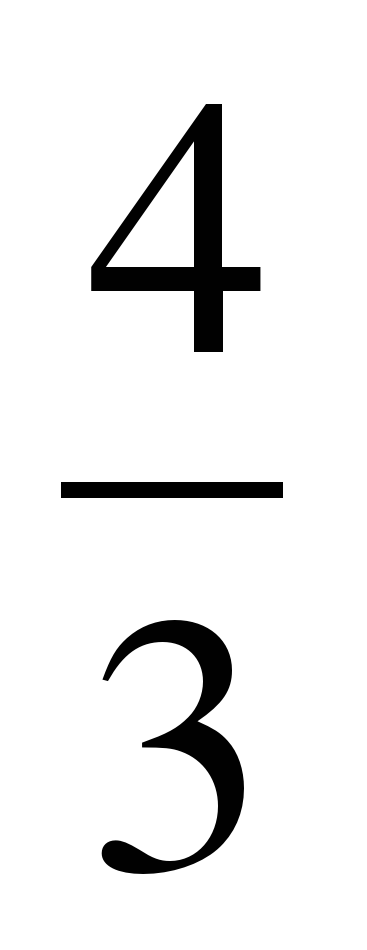
 ”; «центр кола вписаного у трикутник, є точкою перетину його бісектрис» виражають судження. Судження і речення, як бачимо, взаємопов'язані. Однак цей зв'язок не дає підстав для ототожнення їх. Виступаючи в єдності в процесі мислення, кожне з них має свою специфіку і особливості. По-перше, судження відрізняється від речення своїм характером: судження — категорія логічна, ідеальна, а речення — категорія граматична, мовна. По-друге, судження — категорія інтернаціональна, загальнолюдська. Саме ця особливість робить можливим обмін думками між людьми різних націй. Речення природної мови — категорія національна. Воно підлягає специфічним законам граматики певної національної мови. По-третє, судження за структурою завжди тричленне: воно складається з суб'єкта, предиката і зв'язки. Якщо зв'язка явно не виражена в мові, це ще не означає, що її немає в судженні. Адже саме за допомогою зв'язки встановлюється відношення між предметами і їх властивостями.
”; «центр кола вписаного у трикутник, є точкою перетину його бісектрис» виражають судження. Судження і речення, як бачимо, взаємопов'язані. Однак цей зв'язок не дає підстав для ототожнення їх. Виступаючи в єдності в процесі мислення, кожне з них має свою специфіку і особливості. По-перше, судження відрізняється від речення своїм характером: судження — категорія логічна, ідеальна, а речення — категорія граматична, мовна. По-друге, судження — категорія інтернаціональна, загальнолюдська. Саме ця особливість робить можливим обмін думками між людьми різних націй. Речення природної мови — категорія національна. Воно підлягає специфічним законам граматики певної національної мови. По-третє, судження за структурою завжди тричленне: воно складається з суб'єкта, предиката і зв'язки. Якщо зв'язка явно не виражена в мові, це ще не означає, що її немає в судженні. Адже саме за допомогою зв'язки встановлюється відношення між предметами і їх властивостями.
Висновок: логічне мислення визначається наступними властивостями:
Гранично домінує логічні схеми роздумів;
Лаконізм, свідоме намагання знаходити найкоротший, логічний шлях до досягнення мети;
Чітко визначений хід роздумів по кожному пункту проблеми;
Точність висловлювань своїх умовиводів.
Ці риси логічного мислення сприяють загальному розв’язку креативного мислення, підвищенню їх інтелектуально потенціалу.
Література
1.Виленкин Н.Я., Дуничев К.И., Калужин Л.А. Современные основи школьного курса математики. М.,1980. 240 с.
2.Гетманова А.Д. Логика. М. 1986. 288 с.
3.Осинская В.Н. Формирование умственной культуры учащихся в процессе обучения математике Киев.1989 .192 с.
4.Середа В. Ю. Вчись мислити логічно. Київ 1989 р..176 с.
Фридман Л.М. Турецкий Е.Н. Стеценко В.Я. Как научиться решать задачи. М.1979. 190 с.
40

 Получите свидетельство
Получите свидетельство Вход
Вход



 A
A  B O D C Учні старших класів в процесі навчання висувають різні гіпотези відмічають способи перевірки їх вірності самостійно “відкривають” закони, формули доказують теореми. Для розвитку логічного мислення важливо не тільки ставити проблемне питання, але й спонукати учнів до самостійної, творчої роботи, відкриття нових для них властивостей, закономірностей, а також давати логічне обґрунтування вірності всіх своїх міркувань, та вміти спростовувати хибні умовиводи.
B O D C Учні старших класів в процесі навчання висувають різні гіпотези відмічають способи перевірки їх вірності самостійно “відкривають” закони, формули доказують теореми. Для розвитку логічного мислення важливо не тільки ставити проблемне питання, але й спонукати учнів до самостійної, творчої роботи, відкриття нових для них властивостей, закономірностей, а також давати логічне обґрунтування вірності всіх своїх міркувань, та вміти спростовувати хибні умовиводи. 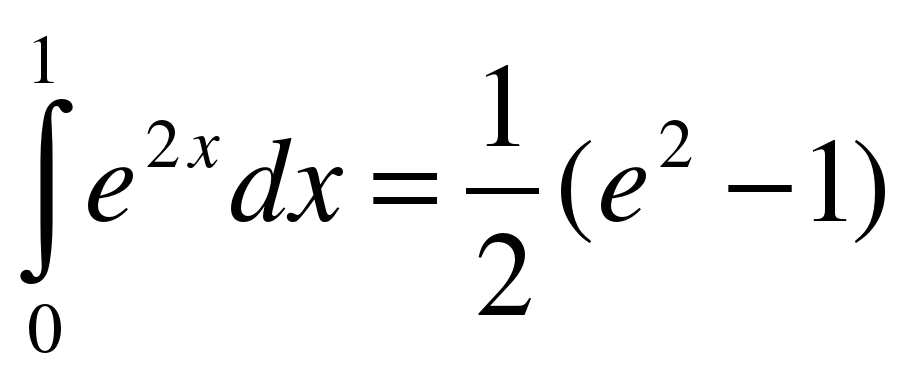 ,
, собливим видом поділу є також класифікація. Тут не бмежуються поділом поняття на класи, а класи поділяють на підкласи, підкласи — на ще дрібніші частини і т. д. Наприклад, алгебраїчні вирази ми І
собливим видом поділу є також класифікація. Тут не бмежуються поділом поняття на класи, а класи поділяють на підкласи, підкласи — на ще дрібніші частини і т. д. Наприклад, алгебраїчні вирази ми І










 Розвиток логічного мислення на уроках математики (0.17 MB)
Розвиток логічного мислення на уроках математики (0.17 MB)
 0
0 1930
1930 300
300 Нравится
0
Нравится
0


