Решение задач по теме "Числовые последовательности" (новое в ОГЭ-2021)

Подготовка к ГИА-2021 в 9 классе

Задание 14. «Числовые последовательности»

По сравнения с прошлыми годами в ГИА – 2021 по математике в 9 классе в задании 14 изменились формулировки задач. Теперь они выглядят как обычные текстовые задачи.

Важно:

1. Если в задаче что-то регулярно возрастает или убывает НА одно и то же число: на одно и то же количество больше или на одно и то же количество меньше, значит, это арифметическая прогрессия.

2. Если в задаче что-то регулярно увеличивается или уменьшается В одно и то же число раз: в одно и то же число раз больше или в одно и то же число раз меньше, значит, это геометрическая прогрессия.

Для решения данных задач нам понадобятся формулы арифметической и геометрической прогрессий (данные формулы имеются в справочных материалах):

1. Формула n-го члена арифметической прогрессии (a_n), первый член которой a₁ и разность равна d: a_{n =} а₁₊ d (n-1).

2. Формула суммы первых n членов арифметической прогрессии: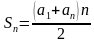

3. Формула n-го члена геометрической прогрессии (b_n), первый член которой b₁, а знаменатель равен q: b_{n =} b_{1 *} q^n-1

4. Формула суммы первых n-членов геометрической прогрессии: S_n =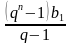

Решим задачи, предложенные в «Открытом банке ОГЭ» на сайте ФИПИ:

Задача 1.

В амфитеатре 10 рядов. В первом ряду 25 мест, а в каждом следующем на 3 места больше, чем в предыдущем. Сколько мест в восьмом ряду амфитеатра?

Решение:

«на 3 места» - значит, имеем дело с арифметической прогрессией

По условию задачи: а_{1 =} 25, d= 3. Найти: а_8.

Воспользуемся формулой: a_{n =} а₁₊ d (n-1).

а₈ = 25 + 3(8-1) = 25+21=46.

Ответ: 46.

Задача 2.

В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 7 минут.

В начальный момент масса изотопа составляла 640 мг. Найдите массу изотопа через 42 минуты.

Ответ дайте в миллиграммах.

Решение:

«уменьшается вдвое» - значит, имеем дело с геометрической прогрессией

По условию задачи: b_{1 =} 640, q= 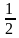(так как масса уменьшается вдвое).

Найти: b₇ (так как n =42 мин : 7 мин + 1=7)_.

Воспользуемся формулой: b_{n =} b_{1 *} q^n-1

b_{7 =} 640 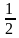_* ( )^7-1= 64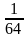0* = 10

Ответ: 10

Задача 3.

В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 13 мг. За каждые 30 минут масса колонии увеличивается в три раза. Найдите массу колонии микроорганизмов через 90 минут после начала эксперимента. Ответ дайте в миллиграммах.

Решение:

«увеличивается в три раза» - значит, имеем дело с геометрической прогрессией

По условию задачи: b_{1 =} 13, q= 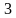. Найти: b₄ (так как n =90 мин : 30мин + 1=4)_.

Воспользуемся формулой: b_{n =} b_{1 *} q^n-1

b_{4 =} 13 _* 3^4-1= 13*27 = 351

Ответ: 351

Задача 4.

Н а клетчатой бумаге с размером клетки 1х1 нарисована «змейка», представляющая из себя ломаную, состоящую из четного числа звеньев, идущих по линиям сетки. На рисунке изображен случай, когда последнее звено имеет длину 10.

Найдите длину ломаной, построенной аналогичным образом, последнее звено которой имеет длину 120.

Решение:

Рассмотрим рисунок и обратим внимание, что самое маленькое звено равно 1 клетке и повторяется дважды, следующее звено равно 2 клетки и также повторяется дважды и так далее. Мы видим, что есть определенная закономерность: 1,1,2,2,3,3,4,4,5,5,6,6,7,7,8,8,9,9,10,10.

Данная последовательность представляет собой арифметическую прогрессию, которая повторяется дважды. Таким образом, чтобы посчитать сумму этой прогрессии, нам нужно будет отделить повторяющиеся числа и посчитать сумму арифметической прогрессии: 1,2,3,4,5….. , а затем умножить ее на 2.

По условию: а_{1 =} 1, d= 1, n=120. Найти: S_120.

Воспользуемся формулой: .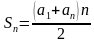

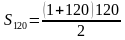= 121*60 = 7260

Теперь полученный результат нужно умножить на 2: 7260*2=14520

Ответ: 14520