Реферат на тему "Алгоритмы построения основных геометрических тел"

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ОБРАЗОВАНИЯ

«МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ

ИМЕНИ М. Е. ЕВСЕВЬЕВА»

Физико-математический факультет

Кафедра информатики и вычислительной техники

РЕФЕРАТ

АЛГОРИТМЫ ПОСТРОЕНИЯ

ОСНОВНЫХ ГЕОМЕТРИЧЕСКИХ ТЕЛ

Выполнила: студентка группы МДИ-114

К. А. Цыганова

Саранск 2018

Основные геометрические тела

Геометрическим телом называется замкнутая часть пространства, ограниченная плоскостями или кривыми поверхностями.

Существует шесть основных геометрических тел, которые лежат в основе строения (конструкции) каждого предмета: куб, конус, пирамида, шар, параллелепипед, цилиндр, тор.

Шар – геометрическое тело, ограниченное поверхностью, все точки которой находятся на равном расстоянии от центра. Образуется из полукруга, вращением вокруг диаметра разреза.

Куб – это правильный многогранник, у которого все грани это квадраты. Куб является частным случаем параллелепипеда и призмы. 4 сечения куба имеют вид правильных шестиугольников — это сечения через центр куба перпендикулярно 4-м главным диагоналям. В кубе насчитывается шесть квадратов. Все вершины куба являются вершинами 3-х квадратов.

Конус – это геометрическая трехмерная фигура, полученная объединением всех лучей, исходящих из вершины конуса и проходящих через плоскую поверхность. Образуется из прямоугольного треугольника, при вращении его вокруг одного из катетов.

Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Образуется из прямоугольника, вращая его вокруг одной из сторон.

Тетраэдр – простейший многогранник, гранями которого являются четыре треугольника, треугольная пирамида. У тетраэдра 4 грани, 4 вершины и 6 рёбер. Тетраэдр, у которого все грани — равносторонние треугольники, называется правильным.

Параллелепипед – это четырехугольная призма, все стороны которой являются параллелограммами или (равносильно) многогранник, у которого шесть граней и каждая из них — параллелограмм. Соответственно, она может иметь только три пары параллельных параллелограммов или шесть граней.

Тор – поверхность вращения, получаемая вращением образующей окружности вокруг оси, лежащей в плоскости этой окружности и не пересекающей её.

Алгоритм построения основных геометрических тел

Этапы построения остроугольной перспективы параллелепипеда:

Провести линию горизонта и восстановить перпендикуляр (любой длины) ближайшего ребра параллелепипеда, пересекающий линию горизонта.

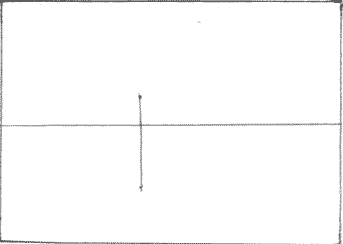
Отметить на линии горизонта две точки схода А и В по разные стороны от ребра-перпендикуляра на любом расстоянии. Соединить концы отрезка, обозначающего ребро параллелепипеда, с точками А и В.

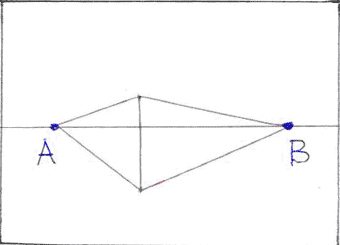
Между линиями соединения восстановить еще два ребра на произвольных расстояниях от ближайшего.

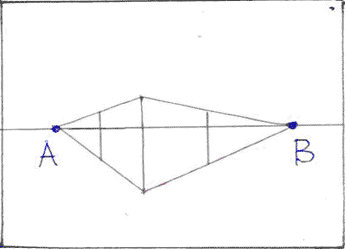
Соединить концы отрезков, обозначающих ребра с теми точками схода, с которыми они еще не соединены. Например, концы отрезка, ближайшего к точке А соединить с точкой В и наоборот. Точки пересечения вновь проведенных линий будут являться вершинами последнего четвертого ребра параллелепипеда.

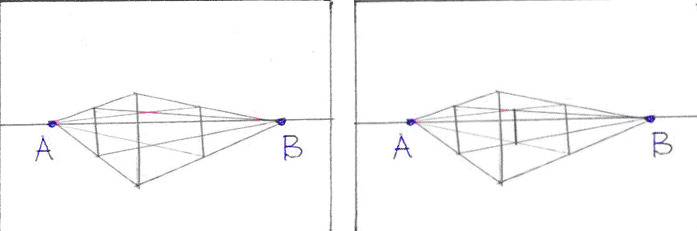
Выявить утолщенными линиями получившееся геометрическое тело, считая его прозрачным, причем видимые ребра выделить жирнее. Обозначить вершины параллелепипеда буквами CDEFGKLM.

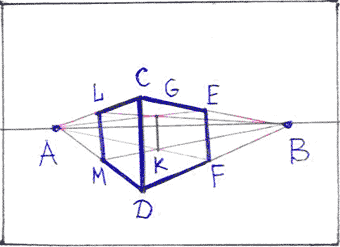
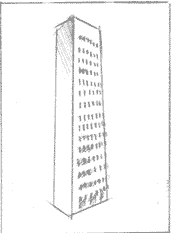
Рассмотреть полученное изображение и отметить, что параллельные в реальной жизни ребра DM, CL, FK, EG сходятся в точке А и на рисунке параллельными не являются. Аналогичная ситуация с другой четверкой ребер DF, CE, MK, LG. Вертикальные же ребра сохраняют свою параллельность и перпендикулярность линии горизонта (так как мы принимаем, что параллелепипед лежит на горизонтальной поверхности и размеры его сравнительно невелики). Сходиться «вертикальные» ребра будут только при отображении длинномерного предмета: например, высотный жилой дом.

Этапы построения цилиндра

На листе А-4 провести вертикальную ось.

Произвольно показать горизонтальные оси, так как предмет строится не с натуры.

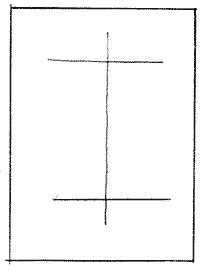
Отметить на горизонтальных осях точки, симметричные относительно вертикальной оси и соответствующие ширине цилиндра (произвольно).

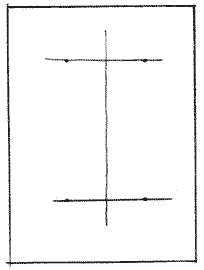
На вертикальной оси, симметрично горизонтальным, отметить еще четыре точки, характеризующие степень раскрытия эллипсов-оснований.

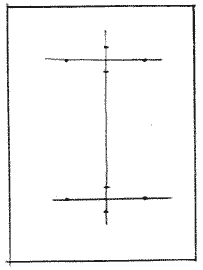
В точках, расположенных на горизонтальных осях, нарисовать четыре «скобки».

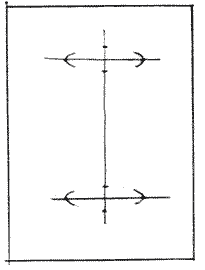
Соединить концы «скобок» и точки, расположенные на вертикальной оси. Придать получившимся фигурам форму правильного эллипса.

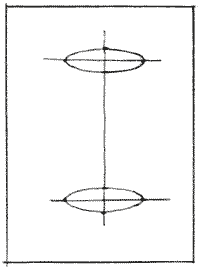
Соединить крайние точки эллипсов, расположенные на горизонтальных осях, вертикальными линиями.

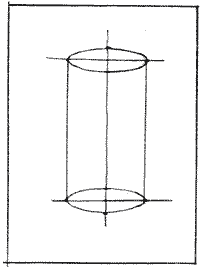
Этапы построения шара:

Провести в центре листа горизонтальную прямую. В ее центре поставьте точку. Через нее проведите прямую перпендикулярно первой, такой же длины.

Отметить на горизонтальных осях точки, симметричные относительно вертикальной оси и соответствующие ширине шара (произвольно). На вертикальной оси, симметрично горизонтальным, отметить еще четыре точки.

Соединить крайние точки получившихся пересекающихся линий, образовывая круг.

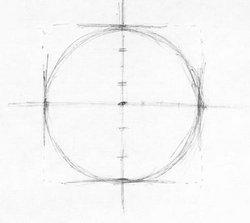
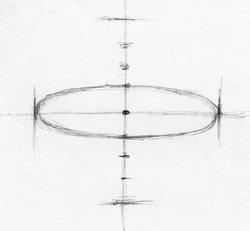
Нарисовать эллипс (овал). Поставить на горизонтали слева и справа от центра и на одинаковом расстоянии от него две точки. Затем отметить на вертикальной линии точками расстояние вдвое или втрое меньшее, чем расстоянии по горизонтали.

Разделить пополам расстояние между верхней границей окружности и центром и ставим в середине точку. Также разделить на равные части расстояние между центром и нижней границей окружности, и тоже отметить середину этого участка точкой. Через поставленные точки провести две линии, параллельные горизонтальной линии, проходящей через центр окружности. Наш круг окажется поделенным на 4 части.

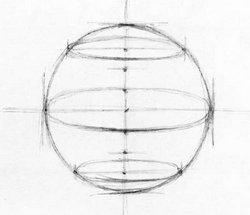
Этапы построения куба:

Взять лист А-4 писчей бумаги. Начать построение с ближайшего ребра.

Далее нарисовать «открытую книжку», учитывая, что пары линий, расположенных по одну сторону от «корешка» обязательно должны сходиться.

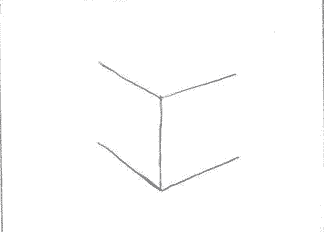
Восстановить перпендикуляры между линиями, идущими по обе стороны от « корешка», тем самым, обозначив две видимые грани и три вертикальных ребра куба.

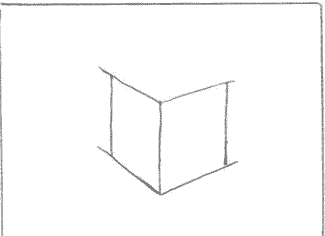
Учитывая основные правила перспективного построения, дорисовать оставшиеся «горизонтальные» ребра куба и, соединив их точки пересечения, получить последнее вертикальное ребро.

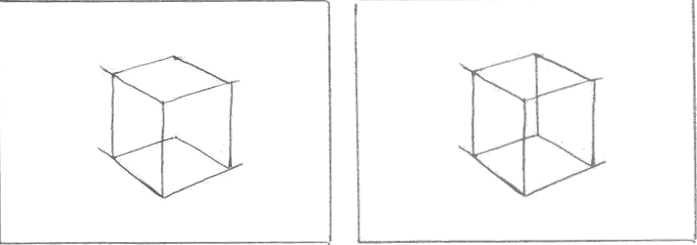
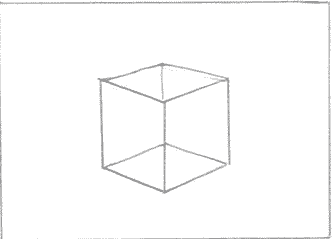
Список использованных источников

1. Геометрия. Учебник. Базовый и профильный уровни. 10-11 классы / Л. С.Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – Москва : Просвещение, – 2016. – 207 с.

2. Глущенко, Ф. Н. Рисунок по представлению [Электронный ресурс] URL: https://www.litres.ru/static/trials/17/19/17/17191709.a4.pdf.

3. Жирных, Б. Г. Начертательная геометрия: учебник. / Под общ. ред. В.И.Серегина – 1-е изд. – М. : Изд-во МГТУ им. Н.Э. Баумана, 2015. – 168 с.

4. Разумова, О. В. Геометрические построения в пространстве: Учебно-методическое пособие / О. В. Разумова, Е. Р. Садыкова. – Казань : Казан. ун-т. – 2014. – 71 с.

5. Рисунок по представлению [Электронный ресурс] URL: https://www.litres.ru/static/trials/17/19/17/17191709.a4.pdf

6. Понятие о перспективе. Простейшие геометрические тела [Электронный ресурс] URL: http://www.mochalova.ru/meth_artterapia/geom_pr.html