План открытого урока по геометрии
в 7 А классе.
Учитель: Евдокимова Л.К.
Тема: РЕШЕНИЕ ЗАДАЧ.
Цель: Закрепить знания по теме «Сумма углов треугольника», научить
применять при решении задач.
Организационный этап.
Проверка домашнего задания .
Разобрать неясные вопросы из д.з.
Теорема 4.4
Математический диктант.
Ответы записаны на доске, ученики пишут в тетрадях только буквы, соответствующие правильным ответам. В результате должно получиться слово « умница»
Существует ли треугольник с двумя прямыми углами?
ДА - А
НЕТ – Т
Существует ли треугольник, два угла которого соответственно равны 120º и 80º?
ДА - Е
НЕТ – ы
Один из углов треугольника тупой. Каковы два остальных?
Прямые - К
Остр. и прям. - Б
Острые – У
Тупой и остр. - А
Существует ли равнобедренный треугольник, два угла которого соответственно равны 30º и 60º?
ДА - Л
НЕТ - М
Один из углов равнобедренного треугольника равен 100º. Чему равны остальные углы?
50º и 50º - О
40º и 40º - Н
40º и 50º - К
100º и 80º - ы
Угол при основании равнобедренного треугольника равен 30º. Чему равен угол при вершине?
120º - И
150º - Н
60º - К
Дано: ∆МКО,
70º - Я
30º - ы
80º - Ц
Дано: ∆АВС,
остроугольный - Б
прямоугольный - А
тупоугольный - В
Так как класс слабый, то после диктанта ученики, у которых правильные ответы, комментируют каждое задание.
Решение задач
№ 22 (3) стр. 63, № 23 (3) стр. 63 (комментир. с места)
№ 28 стр. 63 (сильный ученик у доски)
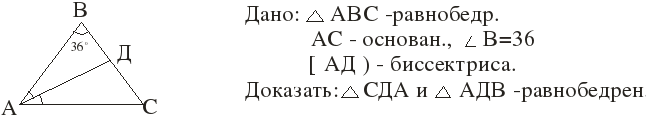
Доказательство:
В ∆ АВД:
∆ АДС:
ч.т.д.
Домашнее задание: №33, №22 (1), №23(1), №24, 27*(1) стр.63
№ 22 (1)
180º - 2*40=100º
№ 23 (1)
(180º - 80º) : 2=50º
№ 24
1). 180º - 100º = 80º
2). 80º : 2 = 40º
№ 27 (1)
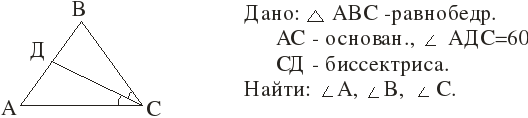
Решение:
Пусть
Значит:
Ответ: 80º, 80º, 20º
Самостоятельная работа (разноуровневая, обучающая) 15 мин.
А(базовый) – те ученики, которые еще не научились выполнять
рисунок по условию.
I В. (1,3,5,7,9,11,13)

План решения:
1). ∆ АВN - … , с основанием … ;
2). ВАN = … как углы при основании равнобедренного треугольника;
3). Сумма углов любого треугольника равна … °;
Следовательно: BАN + АВN + АNВ = … °.
Значит АNВ = … °. 100°
II В. (2, 4, 6, 8, 10, 12, 14)

План решения:
1). ∆ ЕВС - … , с основанием … ;
2). ВСЕ = … как углы при основании равнобедренного треугольника;
3). Сумма углов любого треугольника равна … °;
Следовательно: BЕС + ЕСВ + ЕВС = … °.
Значит ВЕС = … °. 80°
Б (средний) – те ученики, которые могут выполнять рисунок по условию, но не могут выводить следствий.
I В. (15, 17, 19, 21)
В ∆ АВД проведен отрезок ВС так, что АС = ВС, точка С принадлежит отрезку АД. Найти АСВ, если ВАС = 43°.
Карточка «подсказка»
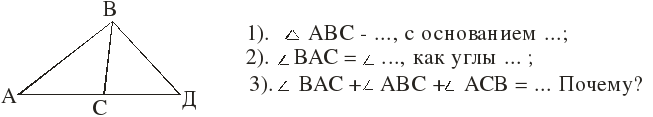
Значит АСВ = … °. 94°
II В. (16, 18, 20, 22)
В ∆ АКЕ проведен отрезок КВ так, чтобы КВ = ВЕ, точка В принадлежит отрезку АЕ. Найти КВЕ, если КЕВ = 32°.
Карточка «подсказка»
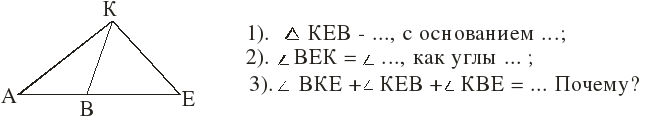
Значит КВЕ = … °. 116°
В (повышенный) (23, 24, 25, 26, 27, 28).
В ∆ АВС проведен отрезок ВД так, что ВД = АД, точка Д принадлежит отрезку АС. Найти ВДС, если А = 28°
Карточка «подсказка»
1). ∆ АВД - … , с основанием … ,
2). АВД = … как углы …,
3). АВД + ВДА + ВАД = … Почему?
Следовательно ВДС = … 56°
Дополнительно: № 27 (2) стр.63
х + 2х +75 = 180, х = 35
Ответ: А = 70°, С = 70°, В = 40°
VII. Итог урока.


 Получите свидетельство
Получите свидетельство Вход
Вход



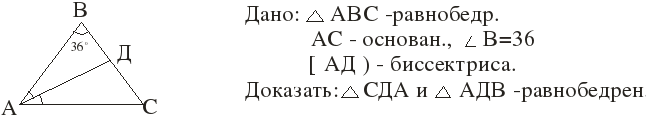
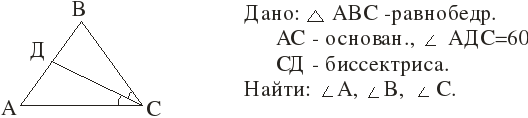


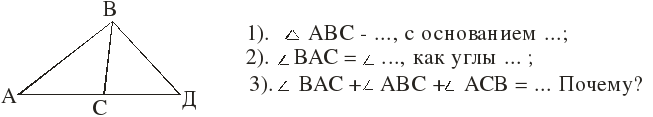
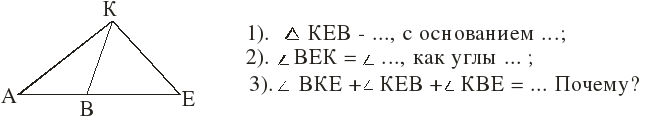









 Разработка урока по математике по теме "Сумма углов треугольника" (0.29 MB)
Разработка урока по математике по теме "Сумма углов треугольника" (0.29 MB)
 0
0 411
411 58
58 Нравится
0
Нравится
0