Цели урока:
образовательная - совершенствовать навыки действий с рациональными дробями; формировать умения выполнять тождественные преобразования рациональных выражений;
воспитательная - воспитывать у школьников любознательность, чувство национальной гордости, патриотизма; создание положительного эмоционального фона на уроке;
развивающая – развивать интерес к математике и её истории, развивать внимание, учить проводить доказательные рассуждения, используя математическую речь; учить умению сосредотачиваться на учебной деятельности и предупреждать ошибки по невнимательности (развивать самоконтроль); развивать творчество учеников.
Этапы урока.
1. Организация начала занятия. Сообщение темы и постановка цели.
2. Актуализация опорных знаний учащихся.
3. Закрепление знаний и способов действий.
4. Информация о домашнем задании, инструкция о его выполнении. (вариативное).
5. Подведение итогов урока.
6.Рефлексия.
7. Физкультурная минутка (развитие двигательной сферы, гимнастика для глаз).
Ход урока.
1. Организация начала занятия.
Сообщение темы и постановка цели. (Слайд № 1)
Если мы откроем Большой Энциклопедический словарь, то сможем прочитать, что обозначает слово «преобразование».
Итак, «Преобразование - замена одного математического объекта аналогичным объектом, получаемым из первого по определенным правилам».
В Толковом Словаре Ожегова читаем: «преобразовать - совершенно переделать, превратить из одного вида в другой, из одной формы в другую…, изменить к лучшему».
Объясните мне, пожалуйста, зачем нужна замена одного математического объекта аналогичным ему объектом?
(Выслушиваются ответы детей.)

Т.о. тождественные преобразования алгебраических выражений представляют собой набор методов, позволяющих быстро и легко упростить сложное выражение и привести его к более компактному.
Целью тождественных преобразований может быть приведение выражения к виду, более удобному для численных расчетов или дальнейших преобразований.
Итак, сегодня на уроке мы будем совершенствовать навыки действий с рациональными выражениями; формировать умения выполнять их тождественные преобразования.
2. Актуализация опорных знаний учащихся.
Ребята, давайте вспомним, какие тождественные преобразования мы знаем.
К тождественным преобразованиям относятся:
приведение подобных членов;
раскрытие скобок;
разложение на множители;
приведение алгебраических дробей к общему знаменателю.
(На этапе актуализации предложен кроссворд на повторение теоретических фактов, необходимых на уроке.)
Приложение2.
У каждого из вас на парте лежит кроссворд. Такой же кроссворд вы видите на экране. Угадав все слова и записав их в клеточки по горизонтали, в выделенном вертикальном столбце вы прочтете одно замечательное слово. (Слайд № 2)
(Разгадав кроссворд, в выделенном вертикальном столбце ученики читают слово «истина»)
Почему мне захотелось выделить это слово?
Потому что мы сегодня познакомимся с фрагментами биографии одной известной женщины-математика, у которой девизом всей жизни было: «служить истине, служить справедливости».
Но знакомиться мы будем в результате выполнения учебных заданий по теме сегодняшнего урока.
3. Закрепление знаний и способов действий.
1) (Слайд № 3)
Кто же эта женщина? Выберите её имя из четырёх имён известных женщин, каждому из которых соответствует набор из единиц и нулей.
Правильному ответу на вопрос соответствует набор, имеющий некоторое отличительное свойство по сравнению с другими наборами.
Ответ: С.В.Ковалевская. Набор (10111) отличается от трёх других тем, что состоит из четырёх единиц и нуля, а другие – из трёх единиц и двух нулей. (Слайд № 4)
Отметим кратко, чьи портреты, помимо С.В.Ковалевской, представлены на слайде.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



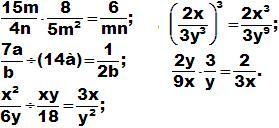
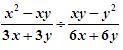
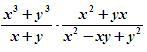
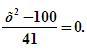
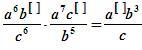
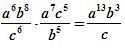









 Разработка урока по математике на тему "Преобразование рациональных выражений" (65.01 КB)
Разработка урока по математике на тему "Преобразование рациональных выражений" (65.01 КB)
 0
0 680
680 95
95 Нравится
0
Нравится
0


