Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №1
Разработка урока по геометрии в 7 классе
«Сумма углов треугольника»
Колтакова Ирина Сергеевна,
учитель математики
2014Тема «Сумма углов треугольника»
Цели урока:
Уметь доказывать теорему, используя различные подходы.
Уметь использовать приобретенные знания и умения в практической деятельности.
Способствовать развитию познавательных и исследовательских умений учащихся, повышению культуры общения.
Содействовать достижению учащимися определенного уровня компетентности в сфере массовых коммуникаций.
Способствовать повышению активности учащихся на уроке, повышению грамотности устной и письменной речи.
Обеспечение:
Microsoft PowerPoint. Презентация «Сумма углов треугольника».
Учебник для общеобразовательных учреждений «Геометрия 7-9». Авторы: Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев Л.С. и др. – М.: Просвещение, 2003.
Интерактивная доска
Компьютер
Проектор
Транспортир, линейка
Структура урока
I. Подготовка учащихся к восприятию нового материала.
Создание проблемной ситуации:
II. Изучение нового материала:
Практическая работа
Доказательство теоремы
III. Закрепление:
IV. Тест
V. Домашнее задание
Ход урока
Подготовка к восприятию нового материала.
Повторение. Устный опрос: (Слайд №4)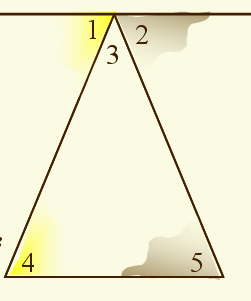
1. Укажите:
а) пару накрест лежащих углов;
б) пару односторонних углов.
2. Свойства накрест лежащих и односторонних углов.
3. Определение равнобедренного треугольника и его свойства.
4. Определение равностороннего треугольника и его свойства
5. Определение развернутого угла и его свойство.Создание проблемной ситуации
Цель работы: создание проблемной ситуации «Чему равна сумма углов треугольника?»
Задание №1. Начертите произвольный треугольник.
Задание №2. Измерьте углы треугольника с помощью транспортира.
Задание №3. Найдите сумму этих углов.
![]()
![]()
![]()
Примерная запись в тетради:
А  А =
А =

 В =
В =
 С =
С =
![]()
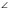 А +
А +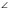 В +
В +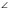 С
С  1800
1800
В С
![]()
Сравнить полученные результаты и выдвинуть предположение.
Учитель: - У всех получился результат, близкий к 1800. Мы с вами рассмотрели 20 разных треугольников и сделаем вывод:
Сумма углов любого треугольника равна 1800.
А небольшие отклонения от этой величины, которые, возможно, у вас получились, связаны с погрешностями при измерении.
II. Изучение нового материала.
Используя гипотезу, что сумма углов в каждом треугольнике равна 180°, выполнить практическую работу.
Практическая работа (Слайд №8)
Опытным путем определите, чему равна сумма углов треугольника.
Необходимое оборудование:
Вырезанный из бумаги произвольный треугольник для каждого ученика.
1. Отогнем один угол треугольника так, чтобы он касался противоположной стороны треугольника, и линия сгиба была параллельна данной стороне. 
2. Второй угол треугольника отогнем так, чтобы он соприкасался с первым углом.

3. Аналогично отогнем третий угол треугольника.
Ответьте на вопросы: (Слайд №9)
Какой угол мы получили?
Чему равна величина этого угла?
Можно ли быть уверенным, что в каждом треугольнике сумма углов равна 180°?
& Записать гипотезу о сумме углов треугольника на доске.
Гипотеза сформулирована. Чтобы она стала истинной, её нужно доказать, убедиться, что она справедлива для любого треугольника.
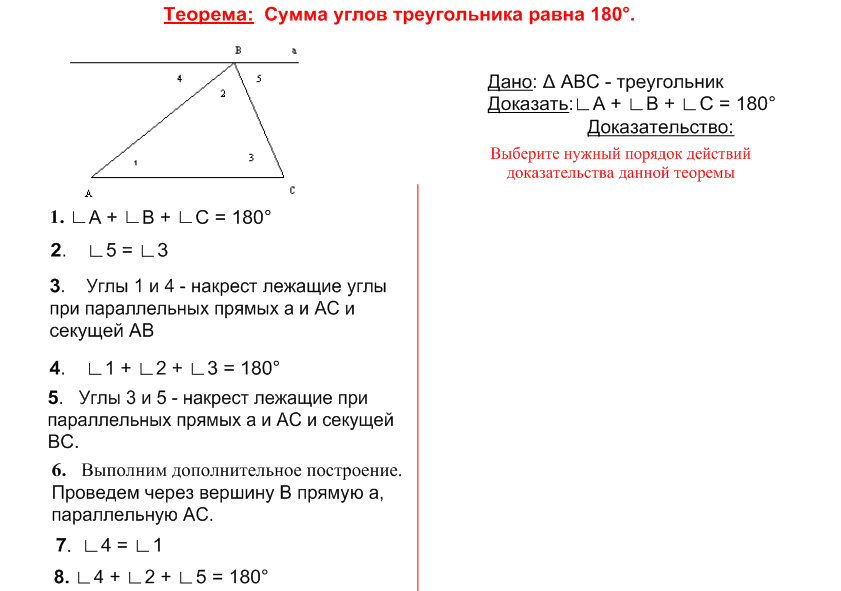
Теорема: Сумма углов треугольника равна 180°.(Слайд №10)
Дано: Δ АВС – треугольник
Доказать: ÐА + ÐВ + ÐС = 180°
Доказательство:
Проведем через вершину В прямую а, параллельную АС.
Углы 1 и 4 – накрест лежащие углы при параллельных прямых а и АС и секущей АВ, а углы 3 и 5 - накрест лежащие при параллельных прямых а и АС и секущей ВС.
Поэтому Ð4 = Ð1, Ð5 = Ð3. (1)
Сумма углов 4, 2 и 5 равна развернутому углу с вершиной В.
Значит, Ð4 + Ð2 + Ð5 = 180°.
Учитывая равенство (1), получаем:
Ð1 + Ð2 + Ð3 = 180° или
ÐА + ÐВ + ÐС = 180°.
С помощью интерактивной доски провести закрепление доказанной теоремы
![]()
![]()
![]()
![]()
Дополнительно для тех, кому интересно: (Слайд №11)
& Есть еще доказательства этой теоремы. Попробуйте свои силы, используя ниже приведенный рисунок и свойство накрест лежащих и односторонних углов при параллельных прямых.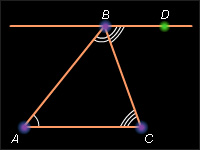
Немного истории (Слайд №12,13)
Первое доказательство было сделано еще Пифагором (V в. до н.э.). 
Великий ученый Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора неизвестно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности.
& Попробуйте доказать дома эту теорему, используя чертеж учеников Пифагора. (Слайд №14)
Внешний угол треугольника (Слайд№14,15)
Определение: Внешним углом треугольника называется угол, смежный с одним из углов треугольника.
Ð 4 – внешний угол Δ АВС
Свойство. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Ð 4 = Ð 1 + Ð 2
По данным равенствам составьте доказательство этого свойства:
Ð 4 + Ð 3 = 180° (почему?),
(Ð 1 + Ð 2) + Ð 3 = 180°(почему?),
Ð 4 = Ð 1 + Ð 2.
III. Закрепление изученного материала
![]()
![]()
![]()
Уровень А
Уровень В
Уровень С
![]()
Устная работа по готовым чертежам (Слайды №18-21)
Классу предлагается решить задачи (текст и рисунки можно заготовить на интерактивной доске, используя затенение экрана – «шторку», за которой спрятаны рисунки к задачам или слайды презентации):
Уровень А (низкий)
Уровень В (средний)
Уровень С (высокий)
(Учитель контролирует работу менее подготовленных учащихся и консультирует по необходимости остальных).
Задача уровня А (Слайды №23,24)
В треугольнике АВС: АВ = ВС, угол А равен 40°. Из вершины В к основанию АС проведена высота. Чему равны углы АСВ, АВD и DВС?
Задача уровня В (Слайды 25-27)
В равностороннем треугольнике АВС проведены биссектрисы АD и ВF, пересекающиеся в точке О. Найдите углы треугольника АОF.
Задача уровня С (Слайды №28)
В равнобедренном треугольнике АВС с основанием АС и углом при основании, равным 72° провели биссектрису АD. Докажите, что треугольники ABD и АDС - равнобедренные.
IV. Тест
I вариант
1. На рисунке ÐА равен:
а) 59°
б) 55°
в) 75°
г) 66°
На рисунке Ð1 равен:
а) 62°
б) 67°
в) 53°
г) определить невозможно
В треугольнике МNK наибольшей стороной является:
а) MN
б) MK
в) KN
г) NK и MN
Равнобедренным является треугольник, изображенный на рисунке:
На рисунке величина угла С равна:
а) 60°
б) 30°
в) 75°
г) нет верного
II вариант
На рисунке ÐС равен:
а) 54°
б) 32°
в) 34°
г) нет верного
На рисунке Ð1 равен:
а) 107°
б) 152°
в) 163°
г) определить невозможно
В треугольнике PKF наибольшим углом является угол:
а) К
б) F
в) P
г) F и P
Равнобедренным является треугольник, изображенный на рисунке:
На рисунке величина угла С равна:
а) 70°
б) 20°
в) 75°
г) нет верного
V. Домашнее задание
П.30, №228(в), №234.
Подготовить карточку к зачету по теме «Сумма углов треугольника».
Другие способы доказательства теоремы о сумме углов треугольника.


 Получите свидетельство
Получите свидетельство Вход
Вход



 А =
А =
 1800
1800















 Разработка урока по геометрии «Сумма углов треугольника» (0.65 MB)
Разработка урока по геометрии «Сумма углов треугольника» (0.65 MB)
 0
0 473
473 33
33 Нравится
0
Нравится
0









