Конспект урока математики
Класс-10
тема «Применение производной при решении прикладных задач».
Автор- учитель математики МОУ « Усогорская СОШ с УИОП»
Усачёва Аделина Олеговна.
Цели урока:
Формирование умений строить доказательство, логическую цепочку рассуждений;
Формирование умений проводить обобщение, переносить знания в новую ситуацию.
Оборудование: компьютер, экран, калькуляторы, мультимедиапроектор.
Организационный этап.
Повторение изученного материала.
Начнем наш урок с разгадывания кроссворда.
|
| 2 |
|
|
|
|
|
|
| П |
|
|
|
|
|
|
| Р |
|
|
|
|
|
| 1 | О |
|
|
| 6 |
|
| К | И |
| 4 |
| У |
|
| А | З |
| Н |
| С |
|
| С | В |
| Е |
| К | 7 |
| А | О | 3 | П |
| О | С |
| Т | Д | А | Р | 5 | Р | Л |
| Е | Н | Р | Е | М | Е | О |
| Л | А | Г | Р | А | Н | Ж |
| Ь | Я | У | Ы | К | И | Н |
| Н |
| М | В | С | Е | А |
| А |
| Е | Н | И |
| Я |
| Я |
| Н | А | М |
|
|
|
|
| Т | Я | У |
|
|
|
|
|
|
| М |
|
|
Вопросы:
Прямая, наиболее тесно примыкающая к кривой в малой окрестности заданной точки.
В математике это понятие возникло в результате попыток придать точный смысл понятию «касательная к кривой в заданной точке».
Приращение какой переменной обычно обозначают 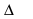
Если существует предел в точке А и этот предел равен значению функции в точке А, то в этой точке функцию называют…
Эта точка лежит внутри области определения функции, и в ней функция принимает самое значение по сравнению со значениями в близких точках.
Эта величина определяется как производная к скорости по времени.
Если функцию у=f(x) можно представить в виде у=f(x)=g(h(x)), где y=g(t) и t=h(x) – некие функции, то функцию f называют…
Кроссворд вы разгадали. В выделенных клетках вы видите фамилию французского математика и механика Жозефа Луи Лагранжа. Он являлся почетным членом Петербургской академии наук. Родился в семье обедневшего чиновника; уже в 19 лет стал профессором в Артиллерийской школе Турина. Именно Лагранж в 1797 году ввёл термин «производная», ему же мы обязаны современным обозначением производной (с помощью штриха). Термин «вторая производная» также ввёл Лагранж.
Наша с вами сегодняшняя задача – более тесно связать понятие производной с задачами практического содержания. Итак, тема урока: «применение производной при решении прикладных задач».
Класс делится на 4 группы. Первая и вторая группы получают одну задачу, третья и четвертая – другую задачу и проводят исследование в поиске решения.
Задача 1
Для размещения склада требуется огородить участок прямоугольной формы наибольшей площади имеющейся для этого сеткой длиной 80м. найдите размеры участка.
Задача 2
Найдите при каких условиях расход жести на изготовление консервных банок цилиндрической формы заданной ёмкости будет наименьшим.
Каждая группа должна составить математическую модель задачи, обсудить и рассмотреть возможные дополнительные условия и затем у доски защитить свои решения.
Учитель выступает в роли консультанта.
Примерные рассуждения учащихся первой и второй групп:
Обозначим длину одной из сторон искомого прямоугольника через х, тогда площадь S(x) прямоугольника выразится формулой: S(x)=x(40-x)=40x-x2, где x принадлежит (0;40)
Исследуя полученную функцию, убеждаемся, что участок наибольшей формы – квадрат 20х20 метров. Наибольшая площадь 400 м2. Учащиеся ввели дополнительное условие: склад строится не на открытом месте, а около каких-либо построек. Какие возможны случаи ограждения склада? Наиболее часто встречаются 2 случая, когда склад примыкает к одной стене или одновременно к двум стенам постройки.
Рассматривая первый случай увидели, что площадь выражается другой формулой: S(x)=2(40x-x2), где х – длина стороны не примыкающей к постройке. Исследуя эту функцию, учащиеся пришли к выводу, что в этом случае оптимальные размеры таковы: длина стороны примыкающей к постройке 40 м, длина другой стороны 20м, а наибольшая площадь 800 м2.
Второй случай показал, что функция S(x)=x(80-x) принимает наибольшее значение при х=40 и S=1600 м2.
Рассмотрение этой задачи ученики сопровождали схемой территории предприятия (компьютер, экран, мультимедиа). Применение схемы позволило последовательно находить оптимальные варианты размещения склада.
Примерные рассуждения учащихся третьей и четвертой групп:
Надо определить размеры цилиндра с Vсм3 так, чтобы площадь его полной поверхности была наименьшей. Обозначим диаметр основания цилиндра через х, а высоту через h. Тогда 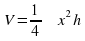 . Отсюда
. Отсюда 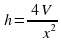 . Полная поверхность цилиндра
. Полная поверхность цилиндра 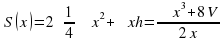 , где
, где 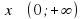 .
.
Найдем производную 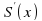 :
: 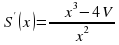 . Для нахождения критических точек решим уравнение
. Для нахождения критических точек решим уравнение 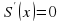 . Корень уравнения
. Корень уравнения 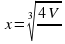 . При
. При 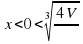
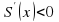 , а при
, а при 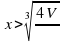
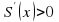 . Следовательно, в точке
. Следовательно, в точке 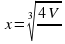 функция имеет минимум. Итак,
функция имеет минимум. Итак, 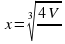 - единственная критическая точка на множестве положительных чисел и является точкой минимума функции, следовательно, функция в этой точке достигает своего наименьшего значения. Таким образом площадь полной поверхности цилиндра, имеющего объём
- единственная критическая точка на множестве положительных чисел и является точкой минимума функции, следовательно, функция в этой точке достигает своего наименьшего значения. Таким образом площадь полной поверхности цилиндра, имеющего объём 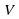 , будет наименьшей при
, будет наименьшей при
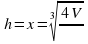 . Таким образом, учащиеся пришли к выводу, то наименьший расход жести на изготовление консервной банки цилиндрической формы заданной емкости будет достигнут при условии, что диаметр основания и высота банки равны между собой. Однако была выдвинута версия, что промышленность не редко выпускает консервы в жестяной таре, не обеспечивая наименьший расход материала на изготовление банки. Это обусловлено рядом причин: стремлением к минимизации отходов при изготовлении банок, соображениями торговой эстетики, возможностями транспортировки.
. Таким образом, учащиеся пришли к выводу, то наименьший расход жести на изготовление консервной банки цилиндрической формы заданной емкости будет достигнут при условии, что диаметр основания и высота банки равны между собой. Однако была выдвинута версия, что промышленность не редко выпускает консервы в жестяной таре, не обеспечивая наименьший расход материала на изготовление банки. Это обусловлено рядом причин: стремлением к минимизации отходов при изготовлении банок, соображениями торговой эстетики, возможностями транспортировки.
Итог урока: сегодня мы с вами узнали, как можно применять производную при решении задач практического содержания.
Домашнее задание:
Установить оптимальные размеры бака (в смысле минимума расходов) данного объёма 0,25м3 с квадратным основанием, если стоимость сварки шва составляет 100руб. за 1 метр, а стоимость жести равна 200 руб. за 1 м2.


 Получите свидетельство
Получите свидетельство Вход
Вход



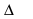
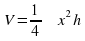 . Отсюда
. Отсюда 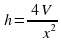 . Полная поверхность цилиндра
. Полная поверхность цилиндра 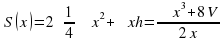 , где
, где 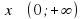 .
.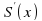 :
: 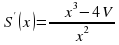 . Для нахождения критических точек решим уравнение
. Для нахождения критических точек решим уравнение 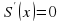 . Корень уравнения
. Корень уравнения 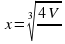 . При
. При 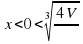
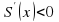 , а при
, а при 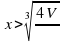
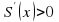 . Следовательно, в точке
. Следовательно, в точке 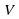 , будет наименьшей при
, будет наименьшей при 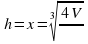 . Таким образом, учащиеся пришли к выводу, то наименьший расход жести на изготовление консервной банки цилиндрической формы заданной емкости будет достигнут при условии, что диаметр основания и высота банки равны между собой. Однако была выдвинута версия, что промышленность не редко выпускает консервы в жестяной таре, не обеспечивая наименьший расход материала на изготовление банки. Это обусловлено рядом причин: стремлением к минимизации отходов при изготовлении банок, соображениями торговой эстетики, возможностями транспортировки.
. Таким образом, учащиеся пришли к выводу, то наименьший расход жести на изготовление консервной банки цилиндрической формы заданной емкости будет достигнут при условии, что диаметр основания и высота банки равны между собой. Однако была выдвинута версия, что промышленность не редко выпускает консервы в жестяной таре, не обеспечивая наименьший расход материала на изготовление банки. Это обусловлено рядом причин: стремлением к минимизации отходов при изготовлении банок, соображениями торговой эстетики, возможностями транспортировки.








 Разработка урока математики по теме "Применение производной" (24.96 КB)
Разработка урока математики по теме "Применение производной" (24.96 КB)
 0
0 416
416 84
84 Нравится
0
Нравится
0


