ГОУ ТО «Советская школа-интернат для детей-сирот и детей, оставшихся без попечения родителей». Учитель математики Балакина Татьяна Николаевна.
___________________________________________________________
Разработка системы итогового повторения
курса алгебры 7-9 х классов
СОДЕРЖАНИЕ:
1. Пояснительная записка.
2. Примерное планирование итогового повторения курса алгебры 7-9-х классов.
3. Тематические тестовые работы (в одном варианте).
4. Обобщающая тестовая работа (в одном варианте).
5. УМК
1. Пояснительная записка
Математика, как всякая наука, представляя собой систему понятий (суждений) и их отношений, имеет свою специфику. Для школьного курса математики характерным является то, что многие понятия не вводятся сразу в полном объеме и содержании. Содержание и объем таких понятий расширяется и обогащается постепенно, по мере развития курса. Достаточно вспомнить понятие числа, функциональной зависимости, геометрической фигуры. Уже в начальной школе учащиеся индуктивным путем знакомятся с этими понятиями. К моменту их изучения в курсах алгебры и геометрии накапливается достаточно материала для их введения на основе систематизации и обобщения. Обобщение и систематизация – неотъемлемое свойство умственной деятельности, лежащее в основе установления существенных взаимосвязей между изучаемыми явлениями, и научного познания вообще.
«Голова, наполненная отрывочными, бессвязанными знаниями,- писал К.Д.Ушинский, - похожа на кладовую, в которой все в беспорядке и где сам хозяин ничего не отыщет; голова, где только система без знания, похожа на лавку, в которой на всех ящиках есть подписи, а в ящиках пусто».
Тематические обобщения и систематизации – должны обеспечить усвоение целой системы или цикла понятий, изучаемых в течение длительного времени, составляющих содержание обширных разделов программы. При организации повторения по содержательно-методическим линиям курса рассматривается ряд ведущих разделов программы: тождественные преобразования выражений, решения уравнений, решение неравенств и т.д. Повторение по содержательно-методическим линиям курса требует использования специально продуманных для этой цели дидактических материалов. Введение государственной итоговой аттестации (ГИА) в новой форме заставило учителей пересмотреть организацию заключительного повторения курса математики.
Проведение итогового повторения по математике ориентировано на подготовку к сдаче итоговой аттестации в виде тестирования, где учащиеся должны продемонстрировать результаты овладения школьного курса математики.
Занятия предназначены для оказания индивидуальной помощи при изучении математики в школе, для восстановления и закрепления знаний, полученных во время изучения той или иной темы, для развития навыков решения широкого круга задач, встречающихся на экзаменах.
Подготовка к итоговой аттестации организована так, чтобы как можно полнее охватить все разделы математики, используемые в тестах на ГИА. На занятиях в доступной форме рассматриваются решения задач и примеров, тематика которых соответствует прототипам заданий, предложенных в демоверсиях. Решение заданий рассматривается подробно, с пошаговым объяснением, методическими рекомендациями и анализом предполагаемых ошибок. Контроль осуществляется с помощью тематических тестов.
Основная цель итогового повторения – повышение качества знаний, умений и навыков, необходимых выпускнику на итоговом тестировании.
Задачи:
- создание прочной и надежной базы, которая поможет учащемуся продемонстрировать определенную системность знаний и широту представлений, умение переходить с одного математического языка на другой, узнавать стандартные задачи в разнообразных формулировках, применять свои знания в практических ситуациях;
- способствование развитию мышления коммуникативной культуры учащихся;
- формирование ответственности за результат итоговой аттестации.
2. Примерное планирование итогового повторения
| № п/п |
Итоговое повторение курса Алгебры 7-9 классов | Кол-во часов |
| 1. | Повторение по теме: «Числа и вычисления». | 2 |
| 2. | Тематическая тестовая работа №1 по теме: «Числа и вычисления». | 1 |
| 3. | Повторение по теме: «Алгебраические выражения». | 2 |
| 4. | Тематическая тестовая работа №2 по теме: «Алгебраические выражения». | 1 |
| 5. | Повторение по теме: «Уравнения. Системы уравнений». | 3 |
| 6. | Тематическая тестовая работа №3 по теме: «Уравнения. Системы уравнений». | 1 |
| 7. | Повторение по теме: «Неравенства. Системы неравенств». | 2 |
| 8. | Тематическая тестовая работа №4 по теме: «Неравенства. Системы неравенств». | 1 |
| 9. | Повторение по теме: «Последовательности и прогрессии». | 1 |
| 10. | Тематическая тестовая работа №5 по теме: «Последовательности и прогрессии». | 1 |
| 11. | Повторение по теме: «Функции». | 2 |
| 12. | Тематическая тестовая работа №6 по теме: «Функции». | 1 |
| 13. | Решение вариантов экзаменационной работы. | 2 |
| 14. | Обобщающая тестовая работа по курсу алгебры 7-9 классов. | 2 |
| 15. | Анализ обобщающей тестовой работы по курсу алгебры 7-9 кл. | 1 |
| 16. | Всего часов: | 23 |
курса алгебры 7-9-х классов
3. Тематические тестовые работы (в одном варианте)
Тематическая тестовая работа №1 по теме: «Числа и вычисления»
Расположите в порядке возрастания числа: 0,0257; 0,205; 0,07.
1) 0,07; 0,205; 0,0257; 3) 0,205; 0,07; 0,0257;
2) 0,0257; 0,205; 0,07; 4) 0,0257; 0,07; 0,205.
2. Какому из данных промежутков принадлежит число 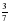 ?
?
1) [0,1; 0,2]; 2) [0,2; 0,3]; 3) [0,3; 0,4]; 4) [0,4; 0,5].
3. Какое из чисел  ,
, 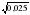 ,
, 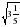 является иррациональным?
является иррациональным?
1)  ; 2)
; 2) 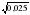 ; 3)
; 3) 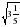 ; 4) все эти числа.
; 4) все эти числа.
4. Какое из чисел отмечено на координатной прямой точкой A?

1)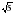 ; 2)
; 2) 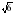 ; 3)
; 3) 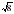 ; 4)
; 4) 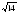 .
.
5. Известно, что х и у – нечётные числа. Какое из следующих чисел также является нечётным?
1) х + у; 2) 4х + у; 3) 4(х + у +1); 4) (х + 2)(у + 1).
6. Какие целые числа заключены между числами √50 и √90?
1) 51,52,…,89; 2) 7, 8, 9, 10; 3) 7, 8, 94 4) 8, 9.
7. Найдите десятичную дробь, равную 56,48 * 10-6.
0,05648; 2) 0,005648; 3) 0,00005648; 4) 0,0000005648.
8. Вычислить ( 5,5 - 2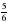 ) : 4 -1.
) : 4 -1.
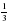 ; 2) -
; 2) - 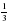 ; 3)
; 3)  ; 4) 9
; 4) 9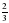 .
.
9. Выразите десятичной дробью 38,5%.
Ответ: _______________________
10. Две трубы наполняют бассейн за 5,3 часа. За какое время наполнят бассейн 5 таких труб (в ч)?
1) 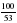 ; 2) 13,25; 3) 2,12; 4) 0,53.
; 2) 13,25; 3) 2,12; 4) 0,53.
Тематическая тестовая работа №2 по теме: «Алгебраические выражения»
Найти значение выражения 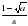 при а = 0,25; в = 0,05.
при а = 0,25; в = 0,05.
Ответ: _____________________________
Найдите значение выражения 0,4х – 1,2х3 при х = -1.
Ответ: _____________________________
Соотнесите выражение с множеством значений переменной с, при которых оно имеет смысл.
А) 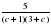 ; Б)
; Б) 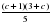 ; В)
; В) 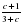 ; Г)
; Г) 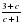 .
.




с -3; 2) с -1; 3) с -3 и с -1; 4) с – любое число.
При каком из указанных значений х выражение  не имеет смысла?
не имеет смысла?
1) х = -4; 2) х = -5; 3) х = 5; 4) х = 0.
За 45 минут человек прошел 4 км. Какое расстояние он пройдет за t минут, если будет идти с той же скоростью?
 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
6. Из формулы площади круга  выразите R.
выразите R.
Ответ: _____________________________
Представьте выражение  в виде степени.
в виде степени.
1) a2; 2) a-4 ; 3) a8 ; 4) a-2.
Найдите значение выражения: (2,4 * 10-3)*(3*10-2).
7200000; 2) 0,00072; 3) 0,000072; 4) 0,0000072.
9. Упростите выражение: (а + 2)2 – (4 – а2).
0; 2) 2а2; 3) 4а; 4) 2а2 + 4а.
10. Разложите на множители квадратный трехчлен: 3х2 + 2х – 1.
Ответ: ____________________________
11. Сократите дробь:  .
.
1) ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
12. Упростите выражение:  :
:  .
.
1) ; 2) -
; 2) - ; 3) -
; 3) -  ; 4)
; 4)  .
.
Тематическая тестовая работа №3 по теме: «Уравнения. Системы уравнений»
Какое из чисел является корнем уравнения: х3 - 2х2 - 4х + 5 = 0?
0; 2) 1; 3) 5; 4) -1.
Линейные функции заданы формулами:
А) у = -10х + 3; Б) у = 15 – 10х; В) у = 5х.
Графики каких функций пересекаются в точке ( ; 1)?
; 1)?
А и Б; 2) А и В; 3) Б и В; 4) нет таких функций.
Найдите корни уравнения: 3 (х – 1) – 2(3х +4) = 1.
-4; 2) -3; 3) 3; 4) 4.
4. Найдите сумму корней уравнения: 4х2 – 12х + 5 = 0.
12; 2) – 3; 3) 3; 4) 1,25.
5. Соотнесите каждое квадратное уравнение и его корни:
А) х2 – 9 = 0 Б) х2 + 2х = 0 В) х2 + 4 = 0
0 и -2; 2) -2 и 2; 3) -3 и 3; 4) нет корней.
6. Решите уравнение: 4х2 – 13х – 12 =0.
0,75 и 4; 2) -0,75 и 4; 3) 0,75 и -4; 4) -0,75 и – 4.
7. Решите уравнение:  .
.
Ответ: ___________________________
8. Найдите решение системы уравнений 
1) (-2; 1); 2) нет решений; 3) (-2; -1); 4) (1; -2).
9. Найдите координаты точки пересечения параболы у = х2 -5х и прямой у = 16 + х.
Ответ: _____________________________
10. Расстояние между пристанями на реке 12 км. Катер проплыл от одной пристани до другой и вернулся обратно, затратив на весь путь 2 ч 30 мин. Какова скорость течения реки (в км/ч ), если собственная скорость катера равна 10 км/ч?
Выберите уравнение, соответствующее условию задачи, если буквой х обозначена скорость течения реки (в км/ч).
1) ; 2) х =
; 2) х =  ; 3)
; 3)  ; 4)
; 4)  .
.
Тематическая тестовая работа №4 по теме: «Неравенства. Системы неравенств».
1. На координатной прямой отмечены числа х, у и z. Какая из следующих разностей
отрицательна?

1) х – у 2) у – х 3) z – у 4) z – х
2. О числах а и в известно, что а Какое из следующих неравенств неверно?
1) а +7 в + 7; 2) а – 5 в – 5; 3)  а в; 4) -
а в; 4) - .
.
3. Решите неравенство: 3 – х  3х + 5.
3х + 5.
1) (-∞; -0,5]; 2) [-0,5; +∞); 3) (-∞; -2]; 4) [-2; +∞).
4. Решите неравенство 8х + 12 4 – 3(4 – х).
1) х -4; 2) х х -5,6; 4) х
Для каждой системы неравенств укажите номер рисунка, на котором изображено
множество её решений.
 А)
А)  1)
1) 
Б)  2)
2) 
В)  3)
3) 
4) 
6. Решите неравенство: 3х2 – 7х + 2 0.
1) решений нет; 2) (-∞; 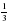 ) U (2; +∞); 3) (
) U (2; +∞); 3) (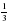 ; 2); 4) (-∞; 2).
; 2); 4) (-∞; 2).
7. Решите графически неравенство х2 + х -1 0
0
Ответ: ______________________________
Тематическая тестовая работа №5 по теме: «Последовательности и прогрессии»
1. Числовая последовательность задана следующими условиями:
а1 = 2; аn+1 = 3аn – 2. Найдите пятый член этой последовательности.
1) 64; 2) 71; 3) 81; 4) 82.
2. Каждой последовательности поставьте в соответствие формулу n-го члена.
А) 6; 12; 24…; Б) 8; 6; 4…; В) 2; 8; 18…
1) 10 – 2n; 2) аn = 2n2; 3) аn = 2n + 6; 4) аn =  .
.
3. Укажите какая из нижеперечисленных последовательностей является
арифметической прогрессией:
1) 2; 7; 11; 16;…; 2) 5; 8; 11; 13;…; 3) 7; 9; 10; 12;…; 4) 10; 20; 30; 40;…
4. Найдите неизвестный член геометрической прогрессии:
…;  ; х;
; х;  ; …, если
; …, если  ; х;
; х;  - последовательные члены и х 0.
- последовательные члены и х 0.
1) 1; 2)  ; 3)
; 3) ; 4) другой ответ.
; 4) другой ответ.
5. Геометрическая прогрессия (bn) задана условиями: b1, и bn+1 = bn· .
.
Определите формулу n-го члена этой прогрессии.
1) bn =  ; 2) bn =
; 2) bn =  ; 3) bn =
; 3) bn =  ; 4) bn =
; 4) bn =  .
.
7. Найдите сумму первых шести членов арифметической прогрессии,
если а1 = 12, d =3.
1) 117; 2) 81; 3) 78; 4) 39.
8. Сколько положительных членов в последовательности (сn), заданной формулой
Сn = 34 – 4n?
1) 4; 2) 8; 3) 9; 4) 17.
9. Найдите сумму всех натуральных чисел, кратных 9 и не превосходящих 520?
Ответ: ____________________________________
Тематическая тестовая работа №6 по теме: «Функции».
Какая из прямых отсутствует на рисунке?
у = 2х + 3; 2) у = 2х – 3; 3) у = -2х +3; 4) у = -2х – 3;
2. Какая из функций является возрастающей?
у = 6х – 8; 2) у = -2х + 5; 3) у = 7х2; 4) у = -5х2.
3. Функция задана формулой  f(x)= -x2 + 4x -3. Найдите f(1).
f(x)= -x2 + 4x -3. Найдите f(1).
4; 2) 0; 3) 1; 4) 3.
4. Найдите координаты точки пересечения графиков функций у = (х – 3)2 + 1 и у = х2 + 4.
(2; 8); 2) (-2; 8); 3) (1; 5); 4) (3;1).
5. На рисунке изображен график квадратичной функции. Для каждого утверждения укажите, верно оно или нет (Для этого, в таблице с ответами под номером верного утверждения поставьте знак «+», неверного – знак «-».)

 У
У 



 1
1
х
 -1
-1





1) функция убывает на промежутке (-∞;-2]; 2) нули функции -4; 0; -5;
3) f(0) = f(-2) = -5; 4) f(x)
6. Найдите область определения функции у =  .
.
1) х # 1; 2) х # -1; 3) х #  1; 4) х – любое число.
1; 4) х – любое число.
7. Найдите сумму координат точки пересечения графиков функций у =  и у =
и у =  .
.
Ответ: ___________________________________
8. На тренировке в 50-метровом бассейне пловец проплыл 200-метровую дистанцию. На рисунке изображен график зависимости расстояния s (в метрах) между пловцом и точкой старта от времени движения t (в секундах) пловца.
Определите по графику, за какое время пловец преодолел 130 метров.
Ответ: _______________________________________
4. Обобщающая тестовая работа (в одном варианте)
Обобщающая тестовая работа по курсу алгебры 7-9 классов
1. Чему равно значение выражения (1,8∙10 -3 ) ∙ ( 3∙105 )?
1) 5400; 2) 540; 3) 54; 4) 5,4.
2. В саду растут 74 дерева. Из них 21 яблоня. Сколько примерно процентов яблонь растут в саду?
1) 35%; 2) 28%; 3) 3,5%; 4) 0,28%.
3. Известно, что числа а, в и с – отрицательные. Какое из приведенных утверждений верно?
1) ав + с ав + с 0; 3) ав +с = 0; 4) знак ав + с может быть любым.
4. Найдите значение выражения  при х = 0,04, у = 0,49.
при х = 0,04, у = 0,49.
Ответ:____________________________
5. Из формулы площади правильного треугольника S =  выразите длину стороны а.
выразите длину стороны а.
1) а =  ; 2) а =
; 2) а =  ; 3) а = 2
; 3) а = 2 ; 4) а =
; 4) а =  .
.
6. Какое из двойных неравенств не является верным?
1) 4
7. Упростите выражение  .
.
Ответ:______________________
7. Преобразуйте в многочлен выражение а(4а – 1) – (1 – 2а)2 .
1) 3а – 1; 2) – а – 1; 3) 8а2 – 5а -1; 4) – 3а + 1.
8. Решите уравнение  .
.
Ответ: __________________________
9. Соотнесите каждое квадратное уравнение и его корни.
А) 4х2 + 4х – 15 = 0; Б) 2х2 + 7 = 0; В) 4х2 – 9 = 0.
1) – 2,5 и 1,5; 2) – 1,5 и 1,5; 3) 1,5 и - 2,5; 4) корней нет.
10. В какой координатной четверти находится точка пересечения прямых
5х + 4у = - 6 и х + 3у = 1?
1) в I; 2) вo II; 3) в III; 4) в IV.
11. От турбазы до станции турист доехал на велосипеде за 4 ч. На мопеде он смог бы проехать это расстояние за 2 ч. Известно, что на мопеде он едет со скоростью, на 9 км/ч большей, чем на велосипеде. Чему равно расстояние от турбазы до станции?
Выберите уравнение, соответствующее условию задачи, если буквой х
обозначено расстояние (в км) от турбазы до станции.
1) 4(х – 9) = 2х; 2) 4х = 2(х + 9); 3)  ; 4)
; 4)  .
.
12. Решите неравенство 8х + 12 4 – 3(4 – х).
1) х - 4; 2) х х - 5,6; 4) х
13. Решите неравенство х2 – 9  0.
0.
1) (- ∞; - 3] U [3; +∞); 2) [-3; 3]; 3) (-∞; 3]4 4) [- 3; +∞).
14. Фирма «Связь» выпустила в продажу две новые модели телефонов – модель А и модель В. На графиках показано, как эти модели продавались в течении года. (По горизонтальной оси откладывается время, прошедшее с начала продаж – в месяцах, а по вертикальной – число телефонов, проданных за это время – в тыс. шт. ). Сколько всего телефонов этих двух моделей было продано за последние 4 месяца?
Ответ: __________________________
При выполнении заданий 15 – 16 запишите решение.
15. Решите систему уравнений 
16. Найдите сумму отрицательных членов арифметической прогрессии: - 10; - 9,8 …?
АНАЛИЗ
тематической тестовой работы № 2
по теме «Алгебраические выражения»
Дата: . Класс: _______.
Кол-во уч-ся в классе ______чел.
Присутствовало: ____ чел. из них выполняли работу _____ чел.
% выполнения _____ чел.
Получили оценки: «5» - ___чел.; «4» - __ чел.; «3» - __ чел.; «2» - ___ чел.;
% успеваемости (УО) - ______%;
% качества (КО) - ______%;
(% успеваемости = к-во уч-ся, выполнивших работу на «5», «4», «3» / к-во
уч-ся, выполнявших работу; % качества = к-во уч-ся, выполнивших работу на
«5», «4» / к-во уч-ся, выполнявших работу).
II.
№ задания | Допущенные ошибки | Кол-во уч-ся, чел. | Кол-во уч-ся в % |
А1. | Выполнили верно | -
| -
|
Не приступили | -
| -
|
Допустили ошибки: - | -
| -
|
А2. | Выполнили верно | -
| -
|
Не приступили | -
| -
|
Допустили ошибки: - | -
| -
|
А3. | Выполнили верно | -
| -
|
Не приступили | -
| -
|
Допустили ошибки: | -
| -
|
- -
| -
| -
|
А4. | Выполнили верно | -
| -
|
Не приступили | -
| -
|
Допустили ошибки: | -
| -
|
- -
| -
| -
|
А5. | Выполнили верно | -
| -
|
Не приступили | -
| -
|
Допустили ошибки: | -
| -
|
- -
| -
| -
|
А6. | Выполнили верно | -
| -
|
Не приступили | -
| -
|
Допустили ошибки: | -
| -
|
- -
| -
| -
|
А7. | Выполнили верно | -
| -
|
Не приступили | -
| -
|
Допустили ошибки: | -
| -
|
- | -
| -
|
А8. | Выполнили верно | -
| -
|
Не приступили | -
| -
|
Допустили ошибки: | -
| -
|
- -
| -
| -
|
А9. | Выполнили верно | -
| -
|
Не приступили | -
| -
|
Допустили ошибки: | -
| -
|
- -
| -
| -
|
А10. | Выполнили верно | -
| -
|
Не приступили | -
| -
|
Допустили ошибки: | -
| -
|
- -
| -
| -
|
Типичные ошибки _____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Анализ причин проявления ошибок __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________
Методические решения устранения ошибок ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________
Учитель____________________ Подпись _________
Используемая литература:
1. Программы для общеобразовательных учреждений Алгебра 7-9 класс Бурмистрова Т.А. Москва «Просвещение» 2009г.
2. Алгебра: Учеб для 7,8 9 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; Под ред. С.А. Теляковского. – М.: Просвещение,2012г.
3. Л.В.Кузнецова, С.Б. Суворова, Л.О. Рослова. Экзамен для девятиклассников: содержание алгебраической части. edu.1september. ru
4. Кузнецова Л.В. и др. Математика: сборник заданий для подготовки к государственной итоговой аттестации в 9 кл.-М.; Просвещение, 2012г.
5. Алгебра. 50 типовых вариантов экзаменационных работ. Неискашова Е.В. Москва «Астраль» 2010г.
6. Математика 2012. ГИА» Интеллект Центр» 2012г.
7. Экзамен в новой форме. Л.В.Кузнецова «Издательство Астраль» 2012г.
8. Типовые тестовые задания 2013г. И.В.Ященко, С.А. Шестаков. Издательство «Экзамен» 2013г.
9. ГИА – 2012: Экзамен в новой форме: Математика: 9-й кл.: Тренировочные варианты экзаменационных работ для проведения государственной итоговой аттестации в новой форме/авт.-сост. Е.А. Бунимович, Л.В. Кузнецова, Л. О. Рослова, С.В. Суворова, С.А. Шестаков, И. В. Ященко. – М.: АСТ Астрель, 2012г. – 90, [6] с.: ил. – (Федеральный институт педагогических измерений).
10. Алгебра. 9 класс: учеб. для общеобразоват. Учреждений. [Г. В. Дорофеев, С. Б. Суворова, Е. А. Бунимович и др.]; под ред. Г. В. Дорофеева; Рос. акад наук, Рос. акад. образования, изд-во «Просвещение». – 4-е изд., с испр. – М. : Просвещение, 2009г. –304с.: ил. – ( Академический школьный учебник)
11. ГИА 2012г. Математика. 9 класс. Государственная итоговая аттестация (в новой форме). Типовые тестовые задания . И. В. Ященко, С.А. Шестаков, А. С. Трепалин, А. В. Семенов, П. И. Захаров. – М.: Издательство «Экзамен», 2012г. – 63, [1] с. (Серия «ГИА. 9 кл. типовые тестовые задания).
12. Математика. 9-й класс. Подготовка к ГИА – 2012г.: учебно-методическое пособие. Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова. – Ростов -на- Дону: Легион – М., 2011г. – 272 с. – (ГИА – 9).
Электронные ресурсы.
Российский портал открытого образования http://www.openet.edu.ru/
Федеральный институт педагогических измерений http://www.fipi.ru/
Портал информационной поддержки Единого государственного экзамена http://www.ege.edu.ru/
Открытый класс. Сообщество «Мир математики» http://www.openclass.ru/node/2367
Газета "Математика" Издательского дома "Первое сентября" http://1september.ru/
Фестиваль педагогических идей «Открытый урок» («Первое сентября») http://festival.1september.ru/
Единая коллекция цифровых образовательных ресурсов http://school-collection.edu.ru/
ГИА 2013. Открытый банк заданий по математике/ http://www.mathgia.ru:8080/or/gia12/
Карман для математика http://karmanform.ucoz.ru/
Сайт Савченко Е.М http://le-savchen.ucoz.ru/

 Получите свидетельство
Получите свидетельство Вход
Вход



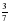 ?
? ,
, 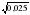 ,
, 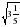 является иррациональным?
является иррациональным?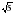 ; 2)
; 2) 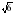 ; 3)
; 3) 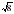 ; 4)
; 4) 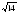 .
.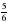 ) : 4 -1.
) : 4 -1.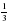 ; 2) -
; 2) -  ; 4) 9
; 4) 9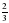 .
.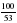 ; 2) 13,25; 3) 2,12; 4) 0,53.
; 2) 13,25; 3) 2,12; 4) 0,53.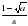 при а = 0,25; в = 0,05.
при а = 0,25; в = 0,05.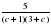 ; Б)
; Б) 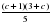 ; В)
; В) 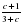 ; Г)
; Г) 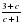 .
.










 Разработка системы итогового повторения за курс алгебры (0.22 MB)
Разработка системы итогового повторения за курс алгебры (0.22 MB)
 0
0 1195
1195 99
99 Нравится
0
Нравится
0






