Разработка практико-ориентированных задач
По данным исследований, в памяти человека остается 25% услышанного материала, 33% увиденного и услышанного, 75% материала, если ученик вовлечен в активные действия в процессе обучения.
Работа с детьми основной школы показала, что уже с 5 класса необходимо знакомить учащихся с алгоритмом решения практико-ориентированных задач.
В каждом параграфе учебника по математике представлены задачи, решение которых рассматривается преимущественно, как средство закрепления теоретического материала. Как показала практика, особый интерес вызывают у детей задачи с практическим содержанием, представляющие собой реальные жизненные ситуации. Поэтому в ходе исследования были разработаны и подготовлены практико-ориентированные задачи для каждой темы, изучающиеся в 8 классе.
Учащиеся, как правило, решают такие задачи после изучения нового материала на этапе закрепления. Решая данные задачи, учащиеся, используют зависимость реальных величин, взятых из жизни. Это позволяет сделать урок более современным, т.к. в это время, дети сами ищут, спорят, сопоставляют, обобщают, делают выводы - одним словом, активно действуют в течении всего урока.
Содержание учебника «Математика 8 класс» авторов Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович и др. (М.: Просвещение, 2010) включает следующие главы [10]:
I. Алгебраические дроби;
II. Квадратные корни;
III. Квадратные уравнения;
IV. Системы уравнений;
V. Функции;
VI. Вероятность и статистика.
Приведены для примера несколько составленных практико-ориентированных задач.
Алгебраические дроби;
Ученик, отработав в школьной трудовой бригаде две недели, получил заработную плату, и решил положить ее на счет в банке. Он может открыть счет с годовым доходом 8%. Если бы банк выплачивал 11% годовых, то для получения такого же дохода потребовалось бы на 900 рублей меньше. Определите, сколько рублей составила заработная плата.
Ответ: 3300р.
Два ученика вместе могут набрать текст на компьютере за 2 ч. Первому ученику на эту работу потребовалось бы на 3 ч больше, чем второму. За какое время может набрать текст на компьютере первый ученик?
Ответ: за 6 часов
Путь от Кыштыма до Екатеринбурга автомобиль проезжает за 2.5 часа. Если он увеличит скорость на 20 км/ч, то за 2 ч он проедет путь на 15 км больший, чем расстояние от Кыштыма до Екатеринбурга. Найдите это расстояние.
Ответ: 125 км
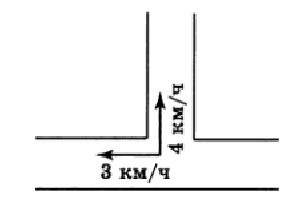
Татьяна прошла от дома до школы и вернулась обратно, затратив на весь путь 1 час. О дома до школы она шла со скоростью 4 км/ч, а на обратном пути ее скорость была 6 км/ч. Чему равно расстояние от дома Тани до школы.
Ответ: 2,4 км
Расстояние между г. Кыштымом и г. Касли равно 30 км. Из г. Кыштыма в направлении г. Касли выехал мотоциклист со скоростью 40 км/ч. Одновременно из города Касли в ом же направлении выехал велосипедист со скоростью 10 км/ч. На каком расстоянии от г. Касли мотоциклист догонит велосипедиста.
Ответ: 10 км
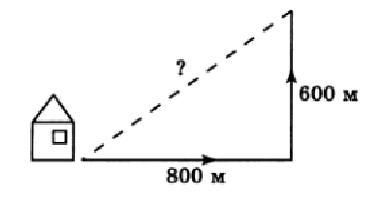
Квадратные корни;
|
|
|
|
|
|
|
|
|
|
Квадратные уравнения;
Пришкольный участок прямоугольной формы площадью 600 кв.м обнесен забором длинна которого 100 м Чему равны стороны участка?
На уроке технологии учащиеся 8 класса из металлического листа, имеющего форму прямоугольника, длина которого в 1,5 раза больше ширины, сделали открытый сверху ящик. Для этого по углам листа вырезали квадраты со стороной 3 дм. и получившиеся боковые грани загнули. Найдите размеры листа, если объем получившегося ящика оказался равным 216 куб.дм.
Системы уравнений;
Волейбольная площадка прямоугольной формы имеет площадь 720 кв.м. Длина ограждения площадки 108 м. Найдите ее размеры.
Ответ: 24 и 30 м
В школьной столовой в понедельник было продано 56 пирожков и 20 стаканов чая на сумму 872 р., а во вторник – 50 пирожков и 40 стаканов чая на 1000 р. Определите цену одного пирожка и одного стакана чая.
Ответ: 12 р. пирожок, 10 р. стакан чая
Для проведении опыта на уроках химии учащийся 8 класса смешал 4%-ный и 10%-ный растворы некоторого химического вещества и получил 75 мл 8%-ного раствора этого вещества. Сколько миллилитров 4%-ного и сколько миллилитров 10%-ного растворов было взято.
Ответ: 25 мл 4%-ного и 50 мл 10%-ного
V. Функции
|
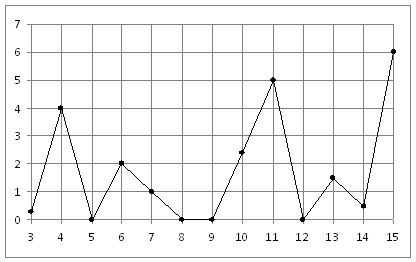
| Определите по рисунку, какого числа впервые выпало 5 миллиметров осадков.
Ответ: 11 февраля. |
На рисунке жирными точками показано суточное количество осадков, выпадавших в Кыштыме с 3 по 15 февраля 2018 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией.
На диаграмме показана среднемесячная температура воздуха в Тайгинке за каждый месяц 2017 года. По горизонтали указываются месяцы, по вертикали - температура в градусах Цельсия.
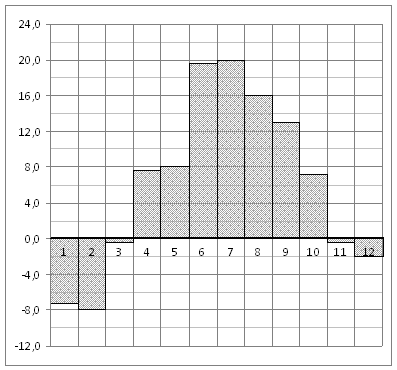
Определите по диаграмме, в течение какого количества месяцев среднемесячная температура не превышала 4 градусов Цельсия.
Ответ: 5 месяцев.
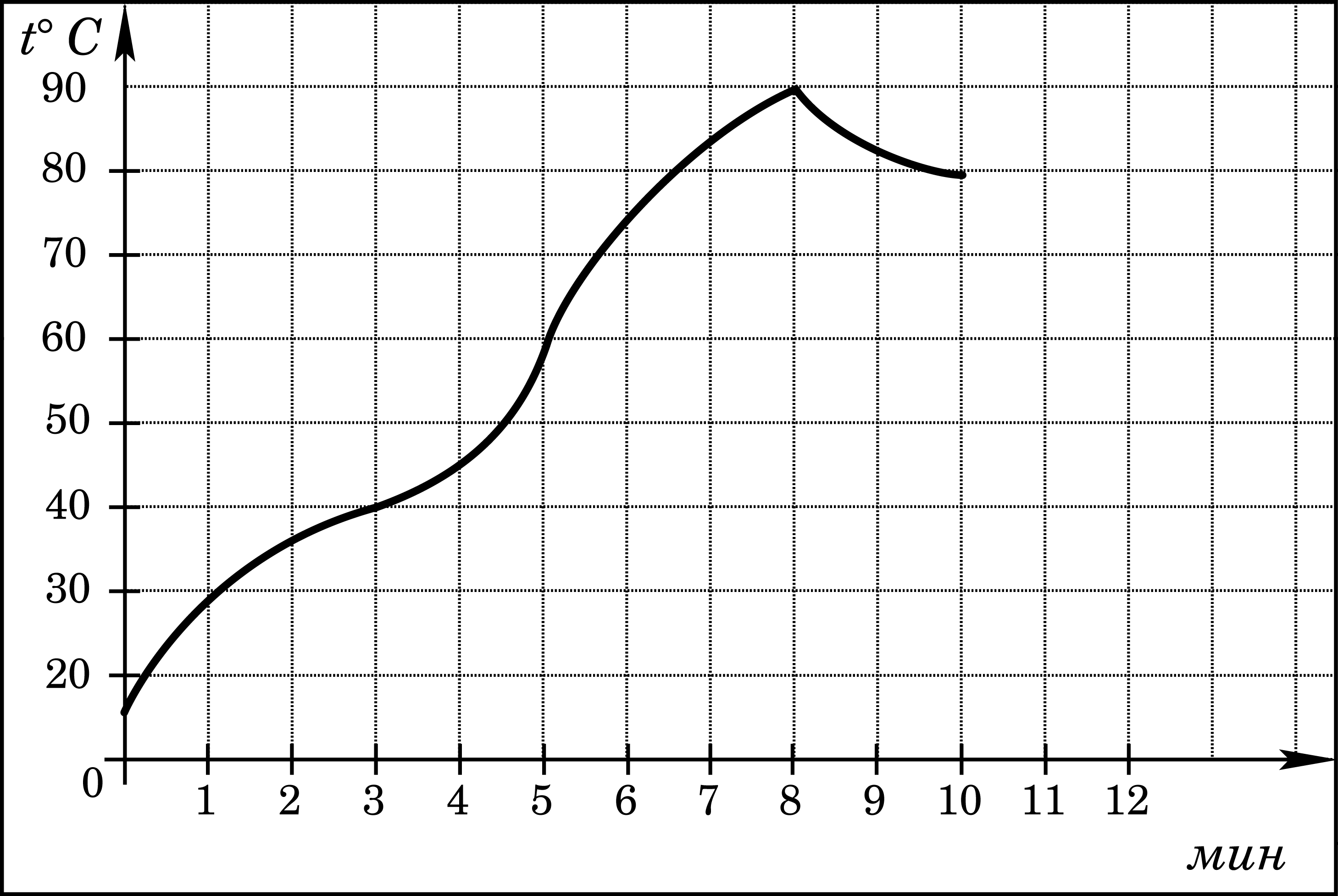
На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат — температура двигателя в градусах Цельсия.
|
| Определите по графику, сколько часов двигатель нагревался от температуры 40 градусов до температуры 90 градусов.
Ответ: 1/12 ч. |
|
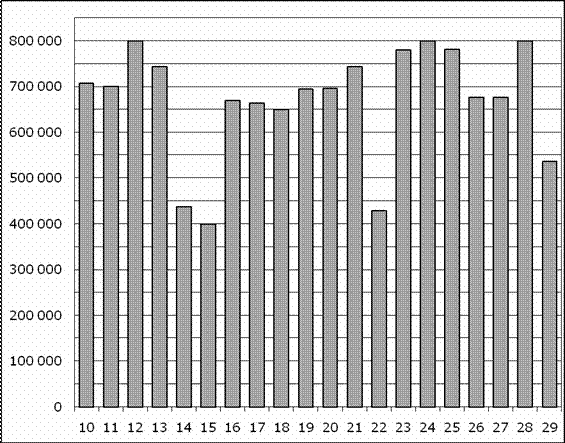
| Определите по диаграмме, какого числа количество посетителей сайта mathege.ru было наименьшим за указанный период
Ответ: 15 ноября. |
4. На диаграмме показано количество посетителей сайта mathege.ru во все дни с 10 по 29 ноября 2018 года. По горизонтали указываются дни месяца, по вертикали — количество посетителей сайта за данный день.
|
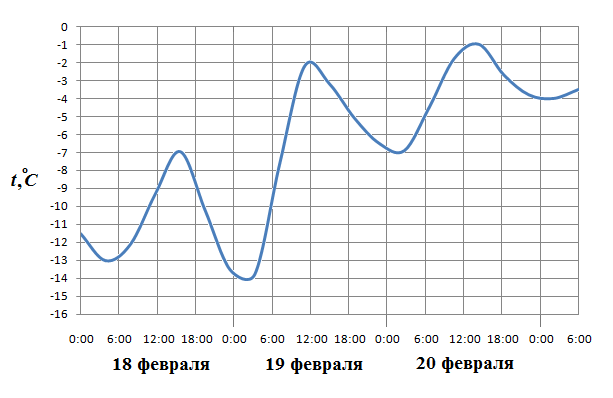
| Определите по рисунку разность между наибольшей и наименьшей температурами воздуха 19 февраля. Ответ дайте в градусах Цельсия.
Ответ: 12С. |
5. На рисунке показано изменение температуры воздуха в Кыштыме на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия.
VI. Вероятность и статистика.
У 25 восьмиклассников спросили, в каком месяце у них день рождения. Вот что получилось:
| Месяц | 1 | 3 | 5 | 6 | 7 | 9 | 10 | 12 |
| Число учащихся | 2 | 2 | 2 | 1 | 4 | 5 | 4 | 5 |
Определите размах, моду, среднее арифметическое выборки, постройте полигон частот.
В коробке лежит 8 красных, 2 синих и 20 белых мелков. Учащийся у доски достает один из мелков. Какова вероятность того, что этот мелок красный? синий? Не белый? Какое наименьшее количество мелков нужно достать, чтобы с вероятностью, равной 1, среди них оказался белый мелок.
Для школьного новогоднего вечера напечатали 90 пронумерованных пригласительных билетов, между которыми будет разыгрываться главный приз. Какова вероятность того что счастливый номер оканчивается:
А) цифрой 5? Б) цифрой 0?
В) У Ольги пригласительный билет с номером 25, а у Артема с номером 90. Верно ли, что у Ольги больше шансов получить главный приз, чем у Артема?
4. Грани кубика желтого, красного и синего цвета. Вероятность выпадения желтой грани при подбрасывании кубика равна 1/6, красной – 1/2. Сколько у кубика желтых, красных и синих граней?
5. Зимой 2018 года в г. Кыштыме относительная частота простудных заболеваний составила 12% - это 4200 человек. Сколько человек проживает в г. Кыштыме.
Как показывает практика, применение данных задач на уроках математики делают урок более интересным. Практико-ориентированные задачи используются на уроках с разной дидактической целью. Они заинтересовывают и мотивируют учащихся, развивают умственную деятельность, объясняют соотношение между математикой и другими дисциплинами.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Разработка практико-ориентированных задач (математика 8 класс) (264 KB)
Разработка практико-ориентированных задач (математика 8 класс) (264 KB)
 0
0 2085
2085 144
144 Нравится
0
Нравится
0


