Разноуровневые индивидуальные домашние задания по теме: «Логарифмическая функция» 10 класс.
Учитель:
ГБОУ ЛНР «Ровеньковская
Специализированная Школа №3»
Литвин Л. Н.
| № | Средний уровень | Достаточный уровень. (Решить уравнение) | Высокий уровень. (Решить неравенство). |
| 1 | а). Вычислить:
|
|
|
| б). Найти область определения функции: | |||
| 2 | а). Чему равно значение выражения: |
|
|
| б). Найти область определения функции: | |||
| 3 | а). Вычислите:
|
| log2x+log2(x-1) ≤1 |
| б). Найти область определения функции: | |||
| 4 | а). Вычислить: |
| log0,5x+log0,5(x+1) ≥1 |
| б). Решите неравенство: | |||
| 5 | а). Вычислить: |
| log0,3 |
| б). Найти область определения:
| |||
| 6 | а). Вычислите: |
| log0,5 |
| б). Найти область определения функции: | |||
| 7 | а). Найти область определения функции: |
| log0,5(x2+3x) ≥-2 |
| б). Вычислить: | |||
| 8 | а). найти область определения функции: |
| log4(x2-6x+8)0,5 |
| б). Вычислить: | |||
| 9 | а). Решить неравенство: |
| log2(x2+3x)≤2 |
| б).Вычислить: | |||
| 10 | а). Решить неравенство: | 1). | log0,2(x2+4x) ≥-1 |
| б). Вычислить: | |||
|
11 |
а). Вычислить: |
. |
log0,5(x2+x) ≥-1 |
| б). Найти область определения функции: | |||
| 12 | а). Вычислить:
| . | log |
| б). Найти область определения функции: | |||
| 13 | а). Вычислить: ; |
| log0,2(x2-2x-3) ≥-1 |
| б). Найти область определения функции: | |||
| 14 | а). Вычислить: |
| log5(x2+2x-3)≤1 |
| б). Найти область определения функции: | |||
| 15 | а). Вычислить: | | log0,1(x+1)log0,1(5-x) |
| б). Найти область определения функции: | |||
| 16 | а). Вычислить: б). Найти область определения функции: |
| log0,5(2x-4)log0,5(x+1) |

 Получите свидетельство
Получите свидетельство Вход
Вход



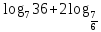 ;
;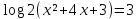 .
.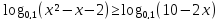 .
.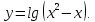
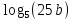 , если
, если 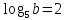 ?
?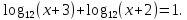
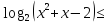
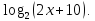
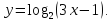
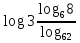
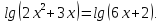
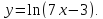
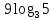 ;
;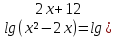 ).
). 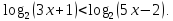
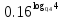
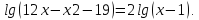
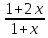 1
1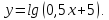
 ;
;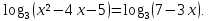
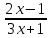 ≥1
≥1 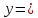 ln(2x+5).
ln(2x+5).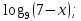









 Разноуровневые индивидуальные домашние задания по теме: «Логарифмическая функция» 10 класс. (23.65 KB)
Разноуровневые индивидуальные домашние задания по теме: «Логарифмическая функция» 10 класс. (23.65 KB)
 0
0 462
462 20
20 Нравится
0
Нравится
0


