Разбор задач по теории вероятности кубики и монеты

Типы задач по теории вероятностей, предлагаемых на ОГЭ

Задачи

на вероятность

с игральным кубиком

(игральная кость)

Задача 1. Игральный кубик бросили один раз. Какова вероятность того, что выпало число очков, большее чем 4?

Решение:

Случайный эксперимент – бросание кубика .

Элементарное событие – число на выпавшей грани .

Всего граней:

Элементарные события:

1, 2, 3, 4, 5, 6

N=6

N(A)=2

Ответ: 1 /3

Реши самостоятельно!

В случайном эксперименте игральный кубик бросают один раз. Найдите вероятность того, что выпадет чётное число.

1, 2, 3, 4, 5, 6

Ответ: 0,5

Реши самостоятельно!

В случайном эксперименте игральный кубик бросают один раз. Найдите вероятность того, что выпадет число, отличающееся от числа 3 на единицу.

1, 2, 3, 4, 5, 6

Ответ: 1/3

Задача2 . Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел нечетна.

Решение :

Сумма будет нечетна, когда: 1) в первый раз выпадет нечетное число, а во второй четное . 2) в первый раз - четное , а во второй раз нечетное .

1) 3 : 6 = 0,5 - Вероятность выпадения нечетного числа в первое бросание.

3 : 6 = 0,5 - Вероятность выпадения четного числа во второе бросание.

0,5 · 0,5 = 0,25 – т.к. эти два события должны произойти совместно . 2) 3 : 6 = 0,5 - Вероятность выпадения четного числа в первое бросание.

3 : 6 = 0,5 - Вероятность выпадения нечетного числа во второе бросание.

0,5 · 0,5 = 0,25 – т.к. эти два события должны произойти совместно.

3) 0,25 + 0,25 = 0,5

Ответ: 0,5

Задача 3. Игральную кость бросают дважды. Найдите вероятность того, что наибольшее из двух выпавших чисел равно 5. Ответ округлите до десятых.

Решение :

1) При первом броске выпадет 1, или 2, или 3, или 4, или 5, а при втором броске выпадет 5 2) При первом броске выпадет 5, а при втором броске выпадет 1, или 2, или 3, или 4, или 5

• 5 : 6 = 5/6 – вероятность того, что выпадут 1; 2; 3; 4; 5

1 : 6 = 1/6 - вероятность выпадения 5

5/6 · 1/6 = 5/36 - вероятность, что произойдут оба события

• 1 : 6 = 1/6 - вероятность выпадения 5

5 : 6 = 5/6 - вероятность выпадения 1; 2; 3; 4; 5

1/6 · 5/6 = 5/36 - вероятность, что произойдут оба события

• 5/36 + 5/36 = 10/36 = 5/18 = 0,277…

Ответ: 0,3

Задачи

на вероятность

с монетами

Задача 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

Решение:

Возможные исходы события:

1 бросок

2 бросок

N=4

О

О

Р

О

N(A)=2

решка - Р

орел - О

О

Р

4 исхода

Р

Р

Ответ: 0,5

Реши самостоятельно!

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что наступит исход ОР (в первый раз выпадет ОРЕЛ, во второй -РЕШКА)

1

О

2

О

О

Р

Р

Р

О

Р

Ответ: 0,25

Реши самостоятельно!

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет ровно 2 раза.

1

О

2

О

О

Р

Р

Р

О

Р

Ответ: 0,25

Реши самостоятельно!

Монету бросают дважды. Найдите вероятность того, что выпадет хотя бы один ОРЕЛ.

1

О

2

О

О

Р

Р

Р

О

Р

Ответ: 0,75

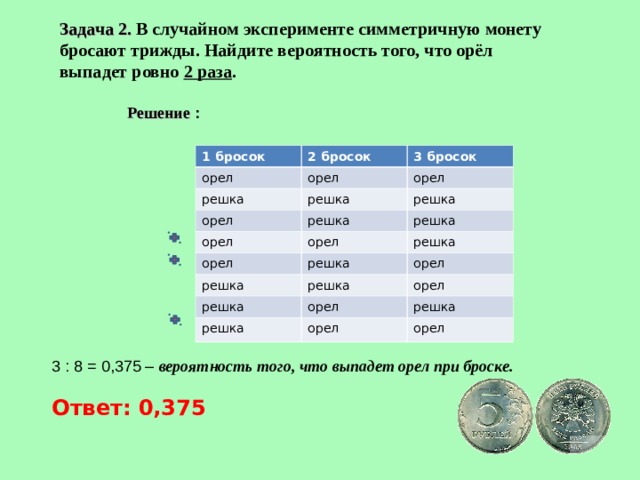
Задача 2. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно 2 раза .

Решение :

1 бросок

2 бросок

орел

орел

решка

3 бросок

решка

орел

орел

решка

решка

орел

орел

орел

решка

решка

решка

решка

решка

орел

решка

орел

орел

решка

орел

решка

орел

3 : 8 = 0,375 – вероятность того, что выпадет орел при броске.

Ответ: 0,375

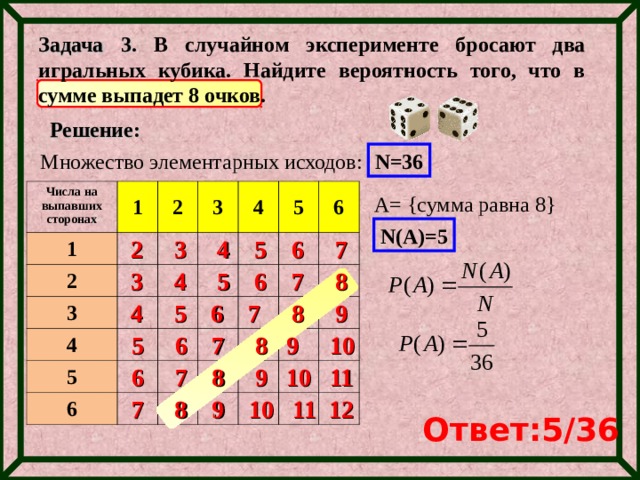
Задача 3. В случайном эксперименте бросают два игральных кубика. Найдите вероятность того, что в сумме выпадет 8 очков.

Решение:

N=36

Множество элементарных исходов:

Числа на выпавших сторонах

1

1

2

2

3

3

4

4

5

5

6

6

A= { сумма равна 8 }

N (А)=5

2 3 4 5 6 7

3 4 5 6 7 8

4 5 6 7 8 9

5 6 7 8 9 10

6 7 8 9 10 11

7 8 9 10 11 12

Ответ:5/36

Реши самостоятельно!

Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию А= { сумма очков равна 5 }

Числа на выпавших сторонах

1

1

2

2

2

3

3

3

3

4

4

4

4

4

5

5

5

5

5

5

6

6

6

6

6

6

6

7

7

7

7

7

7

8

8

8

8

8

9

9

9

9

10

10

10

11

11

12

Ответ: 4

Реши самостоятельно!

Монету бросают три раза. Какова вероятность того, что результаты двух первых бросков будут одинаковы?

1

2

О

О

О

3

О

О

О

Р

Р

О

Р

Р

О

Р

О

Р

О

О

Р

Р

Р

Р

Р

О

Р

Ответ: 0,5