Введение:
Класс: 2
Количество часов: всего 170 часов, в неделю 5 часов
Плановых контрольных уроков - 7, тест - 1
Административных контрольных работ: 3
Планирование составлено на основе Общей образовательной программы начального общего образования, авторской программы «Математика» В.Н. Рудницкой (Образовательная система «Начальная школа XXI века»), авторской программы «Информатика и ИКТ» А.В. Горячева, утвержденной МО РФ, в соответствии с требованиями ФГОС НОО второго поколения (2009г), письма МОиН РТ от 23.06.2012г. №7699/12 «Об учебных планах для I-IХ классов школ Республики Татарстан, реализующих основные образовательные программы начального общего образования и основного общего образования в соответствии с ФГОС общего образования», приказа МОиН РТ от 09.07.2012г. №4154/12 «Об утверждении базисного и примерных учебных планов для образовательных учреждений Республики Татарстан, реализующих программы начального общего образования и основного общего образования».
Учебник: В.Н. Рудницкая, Т.В.Юдачева «Математика», 2 класс, Москва, «Вентана Граф», 2012 год;
Рабочие тетради: В.Н. Рудницкая, Т.В.Юдачева «Математика», 2 части, Москва, «Вентана Граф», 2012 год; А.В. Горячев «Информатика в играх и задачах, 2 части, Москва, «Баласс», 2012 год.
Методическая литература: В.Н. Рудницкая «Методическое пособие «Математика», Москва, «Вентана Граф».
Пояснительная записка
Цели и задачи курса
Важнейшими целями обучения на этом этапе являются:
создание благоприятных условий для полноценного интеллектуального развития каждого ребенка на уровне, соответствующем его возрастным особенностям и возможностям, и обеспечение необходимой и достаточной математической подготовки ученика для дальнейшего обучения;
освоение основ математических знаний, приобретение практических навыков;
способствовать разностороннему и гармоничному развитию, развитию воображения, образного и логического мышления, формированию умения пользоваться алгоритмами;
воспитание интереса к математике, стремление использовать математические знания в повседневной жизни.
Задачи:
овладение умениями наблюдать и выражать в речи свойства предметов, группировать предметы по общим свойствам, складывать и вычитать совокупности предметов;
овладение графическим действием как основой обще учебных умений;
формирование первоначальных математических представлений для описания окружающих предметов, явлений в количественном и пространственном отношении;
развитие умения использовать арифметические способы для разрешения сюжетных ситуаций; работать с алгоритмами выполнения арифметических действий, решения задач, проведение простейших построений;
развитие коммуникативных умений: ориентироваться в книге, участвовать в диалоге, строить монологические высказывания;
воспитание положительной мотивации учения (создание для каждого ребенка ситуации успеха), критичности мышления, интереса к умственному труду, стремление использовать математические знания в повседневной жизни обогащение нравственного опыта младших школьников, формирование представлений о добре и зле, развитие нравственных чувств.
Общая характеристика курса
В программе заложена основа, позволяющая учащимся овладеть определенным объемом математических знаний и умений, которые дадут им возможность успешно изучать математические дисциплины в старших классах. Своеобразие начальной ступени обучения состоит в том, что именно на этой ступени у учащихся должно начаться формирование элементов учебной деятельности. На основе этой деятельности у ребенка возникает теоретическое сознание и мышление, развиваются соответствующие способности (рефлексия, анализ, мысленное планирование); в этом возрасте у детей происходит также становление потребности и мотивов учения.
В основу отбора содержания обучения положены следующие, наиболее важные методические принципы: анализ конкретного учебного материала с точки зрения его общеобразовательной ценности и необходимости изучения в начальной школе; возможность широкого применения изучаемого материала па практике; взаимосвязь вводимого материала с ранее изученным; обеспечение преемственности с дошкольной математической подготовкой и содержанием следующей ступени обучения в средней школе; обогащение математического опыта младших школьников за счет включения в курс новых вопросов, ранее не изучавшихся в начальной школе; развитие интереса к занятиям математикой.
Сформулированные принципы потребовали конструирования такой программы, которая содержит сведения из различных математических дисциплин, образующих пять взаимосвязанных содержательных линий; элементы арифметики; величины и их измерение; логико-математические понятия; алгебраическая пропедевтика; элементы геометрии. Для каждой из этих линий отобраны основные понятия, вокруг которых развертывается все содержание обучения. Понятийный аппарат включает следующие четыре понятия, вводимые без определений: число, отношение, величина, геометрическая фигура.
Некоторые особенности содержания и структуры каждой из содержательных линий.
Формирование первоначальных представлений о натуральном числе начинается в первом классе. При этом последовательность изучения материала такова: учащиеся знакомятся с названиями чисел первых двух десятков, учатся называть их в прямом и в обратном порядке; затем, используя изученную последовательность слов (один, два, три... двадцать), учатся пересчитывать предметы, выражать результат пересчитывания числом и записывать его цифрами.
На первом этапе параллельно с формированием умения пересчитывать предметы начинается подготовка к решению арифметических задач, основанная на выполнении практических действий с множествами предметов. При этом арифметическая задача предстает перед учащимися как описание некоторой реальной жизненной ситуации; решение сводится к простому пересчитыванию предметов. Упражнения подобраны и сформулированы таким образом, чтобы у учащихся нашелся опыт практического выполнения не только сложения и вычитания, по и умножения и деления, что в дальнейшем существенно облегчит усвоение смысла этих действий. На втором этапе внимание учащихся привлекается к числам, данным в задаче. Решение описывается словами: «пять и три - это восемь», «пять без двух это три», «три по два это шесть», «восемь на два - это четыре». Ответ задачи пока также находится пересчитыванием. Такая словесная форма решения позволяет подготовить учащихся к выполнению стандартных записей решения с использованием знаков действий.
На третьем этапе после введения знаков +,-,•.:,= учащиеся переходят к обычным записям решения задач.
При изучении табличных случаев сложения и вычитания используется основной прием вычислений: прибавление (вычитание) числа по частям. Изучение табличных случаев сложения и вычитания нe ограничивается вычислениями в пределах чисел первого десятка: каждая часть таблицы сложения (прибавление чисел 2, 3, 4, ... ) рассматривается сразу на числовой области 1-20.
Особенностью структурирования программы является раннее ознакомление учащихся с общими способами выполнения арифметических действий. При этом приоритет отдается письменным вычислениям. Устные вычисления ограничены лишь простыми случаями сложения, вычитания, умножения и деления, которые без затруднений выполняются учащимися в уме. Устные приемы вычислений часто выступают как частные случаи общих правил.
Обучение письменным приемам сложения и вычитания начинается во 2 классе. Овладев этими приемами с двузначными числами, учащиеся легко переносят полученные умения на трехзначные числа (3 класс) и вообще на любые многозначные числа (4 класс).
Изучение величин распределено по темам программы таким образом, что формирование соответствующих умений производится в течение продолжительных интервалов времени.
Понятие площади фигуры — более сложное. Однако его усвоение удастся существенно облегчить и при этом добиться прочных знаний и умений благодаря организации большой подготовительной работы, начатой во 2 классе. Идея подхода заключается в том, чтобы научить учащихся, используя практические приемы, находить площадь фигуры, пересчитывая клетки, па которые она разбита.
Особенностью структурирования программы является раннее ознакомление учащихся с общими способами выполнения арифметических действии. При этом приоритет отдастся письменным вычислениям. Устные вычисления ограничены лишь простыми случаями сложения, вычитания, умножения и деления, которые без затруднений выполняются учащимися в уме. Устные приемы вычислений часто выступают как частные случаи общих правил.
В целях усиления практической направленности обучения в арифметическую часть программы включен вопрос об ознакомлении учащихся с микрокалькуляторами и их использовании при выполнении арифметических расчетов.
Изучение величин распределено по темам программы таким образом, что формирование соответствующих умений производится в течение продолжительных интервалов времени.
Длина предмета измеряется с помощью шкалы обычной ученической линейки. Одновременно дети учатся чертить отрезки заданной длины (в сантиметрах, в дециметрах, в дециметрах и сантиметрах).
В соответствии с программой учащиеся овладевают многими важными логико-математическими понятиями. Они знакомятся, в частности, с математическими высказываниями, с логическими связками «и», «или», «если ..., то», «неверно, что ...», со смыслом логических слов «каждый», «любой», «все», «кроме», «какой-нибудь», составляющими основу логической формы предложения, используемой в логических выводах.
Важной составляющей линии логического развития ребенка является обучение его действию классификации по заданным основаниям и проверка правильности выполнения задания.
В программе четко просматривается линия развития геометрических представлений учащихся. Дети знакомятся с наиболее распространенными геометрическими фигурами (круг, многоугольник, отрезок, луч, прямая, куб, шар и др.), учатся их различать. Большое внимание уделяется взаимному расположению фигур на плоскости, а также формированию графических
умений - построению отрезков, ломаных, окружностей, углов, многоугольников и решению практических задач (деление отрезка пополам, окружности на шесть рапных частей и пр.).
Большую роль в развитии пространственных представлений играет включение в программу понятия об осевой симметрии. Дети учатся находить на картинках и показывать пары симметричных точек, строить симметричные фигуры.
При выборе методов изложения программного материала приоритет отдается дедуктивным методам. Овладев общими способами действия, ученик применяет полученные при этом знания и умения для решения новых конкретных учебных задач.
Содержание курса
Сложение и вычитание в пределах 100
Чтение и запись двузначных чисел цифрами. Числа 10, 20, 30,…, 100. Решение задач. Запись сложения столбиком. Запись вычитания столбиком. Поразрядное сложение и вычитание двузначных чисел. Числовой луч. Периметр многоугольника. Окружность, ее центр и радиус. Окружность и круг. Взаимное расположение фигур на плоскости.
Таблица умножения однозначных чисел
Табличное умножение чисел и соответствующие случаи деления. Доля числа. Умножение и деление с 0 и 1. Отношения «меньше в…» и «больше в…». Решение задач на увеличение или уменьшение числа в несколько раз.
Площадь фигуры. Единицы площади.
Выражения
Названия чисел в записях действий. Числовое выражение и его значение. Числовые выражения, содержащие скобки. Нахождение значений числовых выражений. Составление числовых выражений. Угол. Прямой угол. Переменная. Выражения с переменной. Решение задач, содержащих переменную. Прямоугольник. Квадрат. Свойства прямоугольника. Площадь прямоугольника.
Геометрические понятия
Форма предмета. Понятия: такой же формы, другой формы. Плоские фигуры: точка, линия, отрезок, ломаная, круг; многоугольники и их виды. Луч и прямая как бесконечные плоские фигуры. Окружность (круг). Изображение плоских фигур с помощью линейки, циркуля и от руки. Угол и его элементы вершина, стороны. Виды углов (прямой, острый, тупой). Классификация треугольников (прямоугольные, остроугольные, тупоугольные). Виды треугольников в зависимости от длин сторон (разносторонние, равносторонние, равнобедренные). Прямоугольник и его определение. Квадрат как прямоугольник. Свойства противоположных сторон и диагоналей прямоугольника. Оси симметрии
прямоугольника (квадрата).
Работа с текстовыми задачами
Понятие арифметической задачи. Решение текстовых арифметических задач арифметическим способом. Работа с текстом задачи: выявление известных и неизвестных величин,составление таблиц, схем, диаграмм и других моделей для представления данных условия задачи.
Планирование хода решения задачи. Запись решения и ответа задачи.
Задачи, содержащие отношения «больше (меньше) на», «больше (меньше) в»; зависимости между величинами, характеризующими процессы купли- продажи, работы, движения тел.
Примеры арифметических задач, решаемых разными способами; задач, имеющих несколько решений, не имеющих решения; задач с недостающими и с лишними данными (не использующимися при решении).
Повторение
«Сложение, вычитание, умножение и деление чисел в пределах 100». «Арифметические задачи». «Выражения с переменной». «Фигуры и величины»
Структура курса
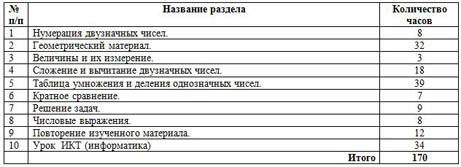
| № п/п | Название раздела | Количество часов |
| 1 | Нумерация двузначных чисел. | 8 |
| 2 | Геометрический материал. | 32 |
| 3 | Величины и их измерение. | 3 |
| 4 | Сложение и вычитание двузначных чисел. | 18 |
| 5 | Таблица умножения и деления однозначных чисел. | 39 |
| 6 | Кратное сравнение. | 7 |
| 7 | Решение задач. | 9 |
| 8 | Числовые выражения. | 8 |
| 9 | Повторение изученного материала. | 12 |
| 10 | Урок ИКТ (информатика) | 34 |
|
| Итого | 170 |
Планируемые результаты усвоения учебного курса
Личностные, метапредметные и предметные результаты освоения курса математики
Личностными результатами обучения учащихся являются:
- самостоятельность мышления; умение устанавливать, с какими учебными задачами ученик может самостоятельно успешно справиться;
-готовность и способность к саморазвитию;
- сформированность мотивации к обучению;
- способность характеризовать и оценивать собственные математические знания и умения;
- заинтересованность в расширении и углублении получаемых математических знаний;
- готовность использовать получаемую математическую подготовку в учебной деятельности и при решении практических задач, возникающих в повседневной жизни;
- способность преодолевать трудности, доводить начатую работу до ее завершения;
- способность к самоорганизованности;
- высказывать собственные суждения и давать им обоснование;
- владение коммуникативными умениями с целью реализации возможностей успешного сотрудничества с учителем и учащимися класса (при групповой работе, работе в парах, в коллективном обсуждении математических проблем).
Метапредметными результатами обучения являются:
- владение основными методами познания окружающего мира (наблюдение, сравнение, анализ, синтез, обобщение, моделирование);
- понимание и принятие учебной задачи, поиск и нахождение способов ее решения;
- планирование, контроль и оценка учебных действий; определение наиболее эффективного способа достижения результата;
- выполнение учебных действий в разных формах (практические работы, работа с моделями и др.);
- создание моделей изучаемых объектов с использованием знаково-символических средств;
- понимание причины неуспешной учебной деятельности и способность конструктивно действовать в условиях неуспеха;
- адекватное оценивание результатов своей деятельности;
- активное использование математической речи для решения разнообразных коммуникативных задач;
- готовность слушать собеседника, вести диалог;
- умение работать в информационной среде.
Предметными результатами учащихся на выходе из начальной школы являются:
- овладение основами логического и алгоритмического мышления, пространственного воображения и математической речи;
- умение применять полученные математические знания для решения учебно-познавательных и учебно-практических задач, а также использовать эти знания для описания и объяснения различных
процессов и явлений окружающего мира, оценки их количественных и пространственных отношений;
- овладение устными и письменными алгоритмами выполнения арифметических действий с целыми неотрицательными числами, умениями
вычислять значения числовых выражений, решать текстовые задачи, измерять наиболее распространенные в практике величины, распознавать и изображать простейшие геометрические фигуры;
- умение работать в информационном поле (таблицы, схемы, диаграммы, графики, последовательности, цепочки, совокупности); представлять, анализировать и интерпретировать данные.
К концу обучения во втором классе ученик научится:
называть:
— натуральные числа от 20 до 100 в прямом и в обратном порядке, следующее (предыдущее) при счете число;
— число, большее или меньшее данного числа в несколько раз;
— единицы длины, площади;
— одну или несколько долей данного числа и числа по его доле;
— компоненты арифметических действий (слагаемое, сумма, уменьшаемое, вычитаемое, разность, множитель, произведение, делимое, делитель, частное);
— геометрическую фигуру (многоугольник, угол, прямоугольник, квадрат, окружность);
сравнивать:
— числа в пределах 100;
— числа в кратном отношении (во сколько раз одно число больше или меньше другого);
— длины отрезков;
различать:
— отношения «больше в» и «больше на», «меньше в» и «меньше на»;
— компоненты арифметических действий;
— числовое выражение и его значение;
— российские монеты, купюры разных достоинств;
— прямые и непрямые углы;
— периметр и площадь прямоугольника;
— окружность и круг;
читать:
— числа в пределах 100, записанные цифрами;
— записи вида 5 · 2 = 10, 12 : 4 = 3;
воспроизводить:
— результаты табличных случаев умножения однозначных чисел и соответствующих случаев деления;
— соотношения между единицами длины: 1 м = 100 см, 1 м = 10 дм;
приводить примеры:
— однозначных и двузначных чисел;
— числовых выражений;
моделировать:
— десятичный состав двузначного числа;
— алгоритмы сложения и вычитания двузначных чисел;
— ситуацию, представленную в тексте арифметической задачи, в виде схемы, рисунка;
распознавать:
— геометрические фигуры (многоугольники, окружность, прямоугольник, угол);
упорядочивать:
— числа в пределах 100 в порядке увеличения или уменьшения;
характеризовать:
— числовое выражение (название, как составлено);
— многоугольник (название, число углов, сторон, вершин);
анализировать:
— текст учебной задачи с целью поиска алгоритма ее решения;
— готовые решения задач с целью выбора верного решения, рационального способа решения;
классифицировать:
— углы (прямые, непрямые);
— числа в пределах 100 (однозначные, двузначные);
конструировать:
— тексты несложных арифметических задач;
— алгоритм решения составной арифметической задачи;
контролировать:
— свою деятельность (находить и исправлять ошибки);
оценивать:
— готовое решение учебной задачи (верно, неверно);
решать учебные и практические задачи:
— записывать цифрами двузначные числа;
— решать составные арифметические задачи в два действия в различных комбинациях;
— вычислять сумму и разность чисел в пределах 100, используя изученные устные и письменные приемы вычислений;
— вычислять значения простых и составных числовых выражений;
— вычислять периметр и площадь прямоугольника (квадрата);
— строить окружность с помощью циркуля;
— выбирать из таблицы необходимую информацию для решения учебной задачи;
— заполнять таблицы, имея некоторый банк данных.
К концу обучения во втором классе ученик может научиться:
формулировать:
— свойства умножения и деления;
— определения прямоугольника и квадрата;
— свойства прямоугольника (квадрата);
называть:
— вершины и стороны угла, обозначенные латинскими буквами;
— элементы многоугольника (вершины, стороны, углы);
— центр и радиус окружности;
— координаты точек, отмеченных на числовом луче;
читать:
— обозначения луча, угла, многоугольника;
различать:
— луч и отрезок;
характеризовать:
— расположение чисел на числовом луче;
— взаимное расположение фигур на плоскости (пересекаются, не пересекаются, имеют общую точку (общие точки);
решать учебные и практические задачи:
— выбирать единицу длины при выполнении измерений;
— обосновывать выбор арифметических действий для решения задач;
— указывать на рисунке все оси симметрии прямоугольника (квадрата);
— изображать на бумаге многоугольник с помощью линейки или от руки;
— составлять несложные числовые выражения;
— выполнять несложные устные вычисления в пределах 100.
Часть базисного учебного плана, формируемая участниками образовательного процесса, отведена на предмет математика для изучения курса Информатики. Такое решение принято из существующих условий образовательного учреждения и запросов обучающихся и их родителей. Предмет «Информатика и ИКТ» предъявляет особые требования к развитию в начальной школе логических универсальных действий и освоению информационно-коммуникационных технологий в качестве инструмента учебной и повседневной деятельности учащихся. В учебно-тематическом планировании этот час обозначен (Урок ИКТ).
Пояснительная записка к курсу информатика
Цели и задачи курса
Цели: овладение первоначальными умениями передачи, поиска, преобразования, хранения информации, использования компьютера;
- поиск (проверка) необходимой информации в словарях, каталоге библиотеки;
- представление материала в табличном виде;
- упорядочение информации по алфавиту и числовым параметрам (возрастанию и убыванию);
- использование простейших логических выражений типа: «…и/или…», «если …, то….», «не только, но и …»;
- элементарное обоснование высказанного суждения;
- выполнение инструкций, точное следование образцу и простейшим алгоритмам.
Задачи: развитие у школьников навыков решения задач с применением таких подходов к решению, которые наиболее типичны и распространены в областях деятельности, традиционно относящихся к информатике;
- алгоритмический подход к решению задач – умение планирования последовательности действий для достижения какой-либо цели, а также решения широкого класса задач, для которых ответом является не число или утверждение, а описание последовательности действий;
- системный подход – рассмотрение сложных объектов и явлений в виде набора более простых составных частей, каждая из которых выполняет свою роль для функционирования объекта в целом; рассмотрение влияния изменения в одной составной части на поведение всей системы;
- объектно-ориентированный подход – акцентирование объектов, а не действий, умение объединять отдельные предметы в группу с общим названием, выделять общие признаки предметов этой группы и действия, выполняемые над этими предметами; умение описывать предмет по принципу «из чего состоит и что делает (можно с ним делать»).
Общая характеристика курса
1.Формирование информационной стороны целостной картины мира, включающей представление об информации и информационных процессах, способах современного развития новых информационных технологий.
2. Освоение терминологии, основных понятий информатики и информационных технологий.
3.Овладение информационной грамотностью, предполагающей умение распознавать потребность в дополнительной информации и стратегию ее поиска, получать, оценивать и использовать недостающую информацию.
4. Формирование представлений о потенциальных возможностях и ограничениях компьютерных технологий.
5. Овладение умениями адекватного применения новых информационных технологий, а также в процессе овладения информационной грамотностью.
Особо следует подчеркнуть актуальность своевременного изучения логических сложных тем на доступном уровне в пропедевтическом курсе информатики.
К основным результатам изучения информатики и ИКТ относятся:
- освоение учащимися системы базовых знаний, отражающих вклад информатики в формирование современной научной картины мира, роль информационных процессов в обществе, биологических и технических системах;
- овладение умениями применять, анализировать, преобразовывать информационные модели реальных объектов и процессов, используя при этом информационные и коммуникационные технологии (ИКТ), в том числе при изучении других школьных дисциплин;
- развитие познавательных интересов, интеллектуальных и творческих способностей путём освоения и использования методов информатики и средств ИКТ при изучении различных учебных предметов;
- воспитание ответственного отношения к соблюдению этических и правовых норм информационной деятельности;
- приобретение опыта использования информационных технологий в индивидуальной и коллективной учебной и познавательной, в том числе проектной, деятельности.
Содержание курса
План действий и его описание
Последовательность действий. Последовательность состояний в природе. Выполнение последовательности действий. Составление линейных планов действий. Поиск ошибок в последовательности действий. Знакомство со способами записи алгоритмов. Знакомство с ветвлениями в алгоритмах.
Отличительные признаки и составные части предметов
Выделение признаков предметов, узнавание предметов по заданным признакам. Сравнение двух или более предметов. Разбиение предметов на группы по заданным признакам. Составные части предметов.
Логические рассуждения
Истинность и ложность высказывании. Логические рассуждения и выводы. Поиск путей на простейших графах, подсчет вариантов. Высказывания и множества. Вложенные множества. Построение отрицания высказываний.
Модуль «Знакомство с компьютером» Компьютеры вокруг нас. Новые профессии. Компьютеры в школе. Правила поведения в компьютерном классе. Основные устройства компьютера. Компьютерные программы. Операционная система. Рабочий стол. Компьютерная мышь. Клавиатура. Включение и выключение компьютера. Запуск программы. Завершение выполнения программы.
Структура курса
| № п/п | Название раздела | Количество часов |
| 1 | План действий и его описание | 11 |
| 2 | Отличительные признаки и составные части предметов | 11 |
| 3 | Логические рассуждения | 12 |
|
| Итого | 34 |
Планируемые результаты усвоения учебного курса
Личностные, метапредметные и предметные результаты освоения учебного предмета
Личностные результаты
К личностным результатам освоения информационных и коммуникационных технологий как инструмента в учёбе и повседневной жизни можно отнести:
критическое отношение к информации и избирательность её восприятия;
уважение к информации о частной жизни и информационным результатам других людей;
осмысление мотивов своих действий при выполнении заданий с жизненными ситуациями;
начало профессионального самоопределения, ознакомление с миром профессий, связанных с информационными и коммуникационными технологиями
Метапредметные результаты
1. Технологический компонент
Регулятивные универсальные учебные действия:
освоение способов решения проблем творческого характера в жизненных ситуациях;
формирование умений ставить цель – создание творческой работы, планировать достижение этой цели, создавать вспомогательные эскизы в процессе работы;
оценивание получающегося творческого продукта и соотнесение его с изначальным замыслом, выполнение по необходимости коррекции либо продукта, либо замысла.
Познавательные универсальные учебные действия:
поиск информации в индивидуальных информационных архивах учащегося, информационной среде образовательного учреждения, в федеральных хранилищах информационных образовательных ресурсов;
использование средств информационных и коммуникационных технологий для решения коммуникативных, познавательных и творческих задач.
Коммуникативные универсальные учебные действия:
создание гипермедиасообщений, включающих текст, набираемый на клавиатуре, цифровые данные, неподвижные и движущиеся, записанные и созданные изображения и звуки, ссылки между элементами сообщения;
подготовка выступления с аудиовизуальной поддержкой.
2. Логико-алгоритмический компонент
Регулятивные универсальные учебные действия:
планирование последовательности шагов алгоритма для достижения цели;
поиск ошибок в плане действий и внесение в него изменений.
Познавательные универсальные учебные действия:
моделирование – преобразование объекта из чувственной формы в модель, где выделены существенные характеристики объекта (пространственно-графическая или знаково-символическая);
анализ объектов с целью выделения признаков (существенных, несущественных);
синтез – составление целого из частей, в том числе самостоятельное достраивание с восполнением недостающих компонентов;
выбор оснований и критериев для сравнения, сериации, классификации объектов;
подведение под понятие;
установление причинно-следственных связей;
построение логической цепи рассуждений.
Коммуникативные универсальные учебные действия:
аргументирование своей точки зрения на выбор оснований и критериев при выделении признаков, сравнении и классификации объектов;
выслушивание собеседника и ведение диалога;
признавание возможности существования различных точек зрения и права каждого иметь свою.
В результате изучения материала учащиеся должны уметь:
-предлагать несколько вариантов лишнего предмета в группе однородных;
-выделять группы однородных предметов среди разнородных и давать названия этим группам;
-разбивать предложенное множество фигур (рисунков) на два подмножества по значениям разных признаков;
-находить закономерности в расположении фигур по значению двух признаков;
-приводить примеры последовательности действий в быту, в сказках;
точно выполнять действия под диктовку учителя;
-отличать высказывания от других предложений, приводить примеры высказываний, определять истинные и ложные высказывания.
Критерии и нормы оценки знаний обучающихся
Особенности организации контроля по математике
Текущий контроль по математике можно осуществлять как в письменной, так и в устной форме. Письменные работы для текущего контроля рекомендуется проводить не реже одного раза в неделю в форме самостоятельной работы или математического диктанта.
Тематический контроль по математике в начальной школе проводится в основном в письменной форме. Для тематических проверок выбираются узловые вопросы программы: приемы устных вычислений, действия с многозначными числами, измерение величин и др.
Среди тематических проверочных работ особое место занимают работы, с помощью которых проверяются знания табличных случаев сложения, вычитания, умножения и деления.
Итоговый контроль по математике проводится в форме контрольных работ комбинированного характера (они содержат арифметические задачи, примеры, задания геометрического характера и др.). В этих работах сначала отдельно оценивается выполнение задач, примеров, заданий геометрического характера, а затем выводится итоговая отметка за всю работу.
При этом итоговая отметка не выставляется как средний балл, а определяется с учетом тех видов заданий, которые для данной работы являются основными.
Классификация ошибок и недочетов, влияющих на снижение оценки
Оценивание письменных работ
В основе данного оценивания лежат следующие показатели: правильность выполнения и объем выполненного задания.
Ошибки:
вычислительные ошибки в примерах и задачах;
ошибки на незнание порядка выполнения арифметических действий;
неправильное решение задачи (пропуск действия, неправильный выбор действий, лишние действия);
не решенная до конца задача или пример;
невыполненное задание;
незнание или неправильное применение свойств, правил, алгоритмов, существующих зависимостей, лежащих в основе выполнения задания или используемых в ходе его выполнения;
неправильный выбор действий, операций;
неверные вычисления в случае, когда цель задания - проверка вычислительных умений и навыков;
пропуск части математических выкладок, действий, операций, существенно влияющих на получение правильного ответа;
несоответствие пояснительного текста, ответа задания, наименования величин выполненным действиям и полученным результатам;
несоответствие выполненных измерений и геометрических построений заданным пара метрам.
Недочеты:
неправильное списывание данных (чисел, знаков, обозначений, величин);
ошибки в записях математических терминов, символов при оформлении математических выкладок;
неверные вычисления в случае, когда цель задания не связана с проверкой вычислительных умений и навыков;
нерациональный прием вычислений;
недоведение до конца преобразований;
наличие записи действий;
неправильная постановка вопроса к действию при решении задачи;
отсутствие ответа к заданию или ошибки в записи ответа.
Оценивание устных ответов
В основу оценивания устного ответа учащихся положены следующие показатели: правильность, обоснованность, самостоятельность, полнота.
Ошибки:
неправильный ответ на поставленный вопрос;
неумение ответить на поставленный вопрос или выполнить задание без помощи учителя;
при правильном выполнении задания не умение дать соответствующие объяснения.
Недочеты:
неточный или неполный ответ на поставленный вопрос;
при правильном ответе неумение самостоятельно или полно обосновать и проиллюстрировать его;
неумение точно сформулировать ответ решенной задачи;
медленный темп выполнения задания, не являющийся индивидуальной особенностью школьника;
За грамматические ошибки, допущенные в работе, оценка по математике не снижается.
За неряшливо оформленную работу, несоблюдение правил каллиграфии оценка по математике снижается на один балл, но не ниже «3».
Характеристика цифровой оценки (отметки)
«5» («отлично») – уровень выполнения требований значительно выше удовлетворительного: отсутствие ошибок как по текущему, так и по предыдущему учебному материалу; не более одного недочета; логичность и полнота изложения.
«4» («хорошо») – уровень выполнения требований выше удовлетворительного: использование дополнительного материала, полнота и логичность раскрытия вопроса; самостоятельность суждений, отражение своего отношения к предмету обсуждения. Наличие 2 – 3 ошибок или 4 – 6 недочетов по текущему учебному материалу; не более 2 ошибок или 4 недочетов по пройденному материалу; незначительные нарушения логики изложения материала; использование нерациональных приемов решения учебной задачи; отдельные неточности в изложении материала.
«3» («удовлетворительно») – достаточный минимальный уровень выполнения требований, предъявляемых к конкретной работе; не более 4 – 6 ошибок или 10 недочетов по текущему учебному материалу; не более 3 – 5 ошибок ли не более 8 недочетов по пройденному учебному материалу; отдельные нарушения логики изложения материала; неполнота раскрытия вопроса.
«2» («плохо») – уровень выполнения требований ниже удовлетворительного: наличие более 6 ошибок или 10 недочетов по текущему материалу; более 5 ошибок или более 8 недочетов по пройденному материалу; нарушение логики; неполнота, нераскрытость обсуждаемого вопроса, отсутствие аргументации либо ошибочность ее основных положений.
Оценка письменных работ по математике.
Работа, состоящая из примеров
«5» – без ошибок.
«4» – 1 грубая и 1 – 2 негрубые ошибки.
«3» – 2 – 3 грубых и 1 – 2 негрубые ошибки или 3 и более негрубых ошибки.
«2» – 4 и более грубых ошибки.
Работа, состоящая из задач
«5» – без ошибок.
«4» – 1 – 2 негрубые ошибки.
«3» – 1 грубая и 3 – 4 негрубые ошибки.
«2» – 2 и более грубых ошибки.
Комбинированная работа
«5» – без ошибок.
«4» – 1 грубая и 1 – 2 негрубые ошибки, при этом грубых ошибок не должно быть в задаче.
«3» – 2 – 3 грубых и 3 – 4 негрубые ошибки, при этом ход решения задачи должен быть верным.
«2» – 4 грубых ошибки.
Контрольный устный счет
«5» – без ошибок.
«4» – 1 – 2 ошибки.
«3» – 3 – 4 ошибки.
«2» – более 3 – 4 ошибок.
Характеристика словесной оценки (оценочное суждение)
Словесная оценка есть краткая характеристика результатов учебного труда школьников. Эта форма оценочного суждения позволяет раскрыть перед учеником динамику результатов его учебной деятельности, проанализировать его возможности и прилежание. Особенностью словесной оценки являются ее содержательность, анализ работы школьника, четкая фиксация успешных результатов и раскрытие причин неудач. Причем эти причины не должны касаться личностных характеристик учащегося.
Оценочное суждение сопровождает любую отметку в качестве заключения по существу работы, раскрывающего как положительные, так и отрицательные ее стороны, а также пути устранения недочетов и ошибок.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по математике (УМК "Школа 21 века") (0.13 MB)
Рабочая программа по математике (УМК "Школа 21 века") (0.13 MB)
 1
1 2300
2300 175
175 Нравится
0
Нравится
0


