ОДП.10
Росрыболовство
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Астраханский государственный технический университет»
Обособленное структурное подразделение «Волго-Каспийский морской рыбопромышленный колледж» федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Астраханский государственный технический университет»
РАБОЧАЯ ПРОГРАММА
дисциплины
ОДП.10 «Математика»
для специальности
080114 «Экономика и бухгалтерский учет (по отраслям)»
Астрахань
2013
|
Одобрена цикловой комиссией естественно-математических дисциплин ФГБОУ ВПО «АГТУ» ОСП «Волго-Каспийский морской рыбопромышленный колледж» Протокол №1 от 29.08.2013
|
|
Разработана на основе примерной программы учебной дисциплины «Математика» для специальности среднего профессионального образования 080114 «Экономика и бухгалтерский учет (по отраслям)»
|
Председатель цикловой комиссии Зам. директора по
естественно-математических дисциплин учебно-производственной работе
Д.В. Земцов И.Д. Кузин
Автор:
Земцов Д.В. – преподаватель Волго-Каспийского морского
рыбопромышленного колледжа
Рецензенты:
Гладченко Л.И. – преподаватель Волго-Каспийского морского
рыбопромышленного колледжа
Панферова Н.А. – преподаватель Астраханского социально-педагогического
колледжа
1. Пояснительная записка
Программа учебной дисциплины «Математика» составлена на основании примерной программы для специальностей среднего профессионального образования. Согласно «Рекомендациям по реализации образовательной программы среднего (полного) общего образования в образовательных учреждениях начального профессионального и среднего профессионального образования в соответствии с федеральным базисным учебным планом и примерными учебными планами для образовательных учреждений Российской Федерации, реализующих программы общего образования», математика в учреждениях среднего профессионального образования изучается с учетом профиля получаемого профессионального образования. Данная программа составлена для специальностей экономического профиля 080114 «Экономика и бухгалтерский учет (по отраслям)», 080118 «Страховое дело (по отраслям)», 100701 «Коммерция (по отраслям)».
Программа ориентирована на достижение следующих целей:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения смежных естественнонаучных дисциплин на базовом уровне и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки;
воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.
В результате изучения учебной дисциплины обучающийся должен
уметь:
выполнять в ходе практической, в том числе профессиональной деятельности практические расчеты по изученным алгебраическим формулам, используя при необходимости справочные материалы, простейшие вычислительные средства;
использовать знания алгебры в практической, в том числе профессиональной деятельности для описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков, для построения и исследования простейших моделей;
использовать знания и умения математического анализа в практической, в том числе профессиональной деятельности для решения прикладных задач;
анализировать реальные числовые данные, представленные в виде диаграмм, графиков, информацию статистического характера;
использовать знания и умения геометрии в практической деятельности и повседневной жизни для исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур, для вычисления объемов и площадей поверхностей пространственных тел;
знать:
значение математической науки для решения задач, возникающих в теории и практике; сферу применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
вероятностный характер различных процессов окружающего мира.
Содержание рабочей программы рассчитано на 290 часов. Распределение часов по разделам и темам программы произведено с учетом экономического профиля профессионального образования. Профилизация целей математического образования для специальностей экономического профиля предполагает усиление общекультурной составляющей дисциплины с ориентацией на визуально-образный и логический стили учебной работы.
В целях эффективной реализации данной программы, формирования общих и профессиональных компетенций обучающихся преподаватель должен использовать современные дидактические приемы и методы (проблемное изложение учебного материала, использование проблемных вопросов и заданий, исследовательское формирование математических понятий, игровые технологии, метод проектов и др.).
При изучении дисциплины «Математика» необходимо обращать внимание обучающихся на ее прикладной характер, на то, где и когда изучаемые теоретические положения и практические навыки могут быть использованы в будущей практической деятельности. Необходимо подчеркивать междисциплинарные связи математического содержания с учебным содержанием: 1) базовых образовательных дисциплин (естествознание, география, ОБЖ); 2) профильных дисциплин (информатика и ИКТ, экономика); 3) общепрофессиональных дисциплин (экономика организации; статистика; финансы, денежное обращение и кредит (для спец. 080114, 080118); налоги и налогообложение (для спец. 080114, 080118); основы бухгалтерского учета (для спец. 080114); бухгалтерский учет в страховых организациях (для спец. 080118); бухгалтерский учет (для спец. 100701)).
Изучение материала необходимо вести в форме, доступной пониманию, а также соблюдать преемственность в обучении, единство терминологии и обозначений в соответствии с действующими государственными стандартами. При проведении занятий следует:
использовать учебные пособия, технические и наглядные средства обучения;
проводить несложные дедуктивные и индуктивные рассуждения;
обосновывать шаги решения задач;
формулировать определения математических понятий;
пользоваться математической терминологией и символикой;
письменно оформлять решение задач;
формулировать на математическом языке несложные прикладные задачи;
пользоваться калькулятором;
самостоятельно изучать учебный материал.
В рабочей программе дисциплины планируется самостоятельная работа обучающихся и указывается ее тематика. Предусмотрены такие виды самостоятельной работы студентов, как решение задач, составление теста, выполнение графической работы, написание рефератов, защита исследовательских проектов.
В содержании учебной дисциплины по каждой теме приведены требования к формируемым умениям и знаниям.
В ходе изучения дисциплины программой предусмотрены 4 контрольные работы, по одной в завершении каждого раздела. Итоговая форма контроля в 1 семестре – письменный экзамен, во 2 семестре – письменный экзамен.
2. Тематический план
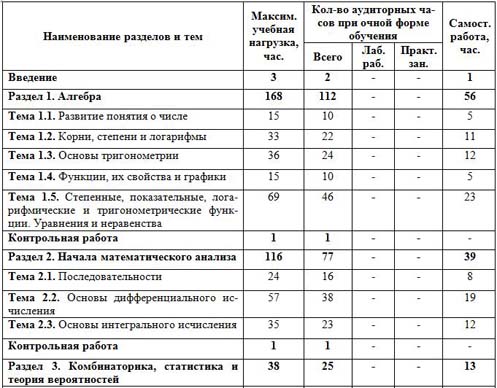
| Наименование разделов и тем | Максим. учебная нагрузка, час. | Кол-во аудиторных часов при очной форме обучения | Самост. работа, час. |
| Всего | Лаб. раб. | Практ. зан. |
| Введение | 3 | 2 | - | - | 1 |
| Раздел 1. Алгебра | 168 | 112 | - | - | 56 |
| Тема 1.1. Развитие понятия о числе | 15 | 10 | - | - | 5 |
| Тема 1.2. Корни, степени и логарифмы | 33 | 22 | - | - | 11 |
| Тема 1.3. Основы тригонометрии | 36 | 24 | - | - | 12 |
| Тема 1.4. Функции, их свойства и графики | 15 | 10 | - | - | 5 |
| Тема 1.5. Степенные, показательные, логарифмические и тригонометрические функции. Уравнения и неравенства | 69 | 46 | - | - | 23 |
| Контрольная работа | 1 | 1 | - | - | - |
| Раздел 2. Начала математического анализа | 116 | 77 | - | - | 39 |
| Тема 2.1. Последовательности | 24 | 16 | - | - | 8 |
| Тема 2.2. Основы дифференциального исчисления | 57 | 38 | - | - | 19 |
| Тема 2.3. Основы интегрального исчисления | 35 | 23 | - | - | 12 |
| Контрольная работа | 1 | 1 | - | - | - |
| Раздел 3. Комбинаторика, статистика и теория вероятностей | 38 | 25 | - | - | 13 |
| Тема 3.1. Элементы комбинаторики | 9 | 6 | - | - | 3 |
| Тема 3.2. Элементы теории вероятностей | 15 | 10 | - | - | 5 |
| Тема 3.3. Элементы математической статистики | 14 | 9 | - | - | 5 |
| Контрольная работа | 1 | 1 | - | - | - |
| Раздел 4. Геометрия | 105 | 70 | - | - | 35 |
| Тема 4.1. Прямые и плоскости в пространстве | 27 | 18 | - | - | 9 |
| Тема 4.2. Многогранники | 18 | 12 | - | - | 6 |
| Тема 4.3. Тела и поверхности вращения | 15 | 10 | - | - | 5 |
| Тема 4.4. Измерения в геометрии | 30 | 20 | - | - | 10 |
| Тема 4.5. Координаты и векторы | 15 | 10 | - | - | 5 |
| Контрольная работа | 1 | 1 | - | - | 1 |
| ИТОГО | 435 | 290 | - | - | 145 |
3. Содержание учебной дисциплины
Введение
После изучения введения обучающийся должен
знать:
История развития математического знания (с древности до наших дней). Математика в науке, технике, экономике, информационных технологиях и практической деятельности. Цели и задачи изучения математики в учреждениях среднего профессионального образования.
Самостоятельная работа
Реферат «История развития математических знаний (в Древнем Египте и Вавилоне, Древней Греции, Древней Индии и Китае, странах ислама; в эпоху Возрождения, эпоху Просвещения, в 19 и 20 веке)» (подбор теоретического материала для написания введения).
Раздел 1. Алгебра
Тема 1.1. Развитие понятия о числе
После изучения темы обучающийся должен
уметь:
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных средств;
вычислять абсолютную и относительную погрешности приближенных значений;
решать текстовые задачи на пропорции и проценты;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для практических расчетов;
знать:
основные числовые множества, их соотношение;
определение действительного числа, абсолютной и относительной погрешности приближений.
Натуральные и целые числа, их делимость. Деление с остатком. Рациональные числа, действия над ними. Обыкновенные и десятичные дроби. Решение задач на проценты и составление пропорций. Иррациональные числа. Множество действительных чисел. Приближенные вычисления, абсолютная и относительная погрешности приближения числа. Комплексные числа.
Самостоятельная работа
Реферат «История развития математических знаний (в Древнем Египте и Вавилоне, Древней Греции, Древней Индии и Китае, странах ислама; в эпоху Возрождения, эпоху Просвещения, в 19 и 20 веке)» (написание и оформление введения).
Решение задач вычислительных примеров, экономических задач на пропорции и проценты и задач на оценку погрешности приближений.
Тема 1.2. Корни, степени и логарифмы
После изучения темы обучающийся должен
уметь:
находить значения корня натуральной степени, степени с рациональным показателем, используя при необходимости вычислительные средства;
находить значения логарифма числа, используя при необходимости переход к новому основанию и вычислительные средства;
применять свойства степени, корня и логарифма для вычисления и упрощения алгебраических выражений;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для практических расчетов по формулам, содержащим степени, радикалы, логарифмы, используя при необходимости справочные материалы, простейшие вычислительные средства;
знать:
определение и свойства корня натуральной степени и степени с рациональным показателем;
понятие логарифма числа, свойства логарифма, частные случаи логарифма (натуральный, десятичный).
Степень с натуральным показателем, ее свойства. Многочлены, действия над ними. Разложение многочлена на множители. Корни многочлена. Корень натуральной степени из числа, его свойства. Степень с целым, рациональным и действительным показателем, ее свойства. Преобразование рациональных и иррациональных выражений. Логарифм числа. Свойства логарифма. Натуральный и десятичный логарифм. Преобразование логарифмических выражений.
Самостоятельная работа
Реферат «История развития математических знаний (в Древнем Египте и Вавилоне, Древней Греции, Древней Индии и Китае, странах ислама; в эпоху Возрождения, эпоху Просвещения, в 19 и 20 веке)» (подбор и изучение литературы, подбор материалов из Интернет – источников, написание и оформление первой и второй главы основной части).
Решение задач с помощью логарифмов.
Тема 1.3. Основы тригонометрии
После изучения темы обучающийся должен
уметь:
вычислять значения тригонометрических выражений, пользуясь формулами, таблицами значений и вычислительными средствами;
выполнять преобразования тригонометрических выражений;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для практических расчетов по тригонометрическим формулам, используя при необходимости справочные материалы и простейшие вычислительные средства;
знать:
формулы перевода градусной меры угла в радианную и обратно;
определение понятий синуса, косинуса, тангенса и котангенса произвольного угла;
основные тригонометрические формулы.
Радианное измерение углов и дуг. Соотношения между градусной и радианной мерами угла. Синус, косинус, тангенс, котангенс произвольного угла, знаки и таблица их значений. Основные тригонометрические тождества. Формулы приведения. Четность и нечетность, периодичность синуса, косинуса, тангенса, котангенса. Формулы сложения. Формулы двойного и половинного аргумента. Преобразование тригонометрической суммы (разности) в произведение и произведения - в сумму (разность). Выражение тригонометрических величин через тангенс половинного аргумента. Вычисление значений и тождественные преобразования тригонометрических выражений.
Самостоятельная работа
Реферат «История развития математических знаний (в Древнем Египте и Вавилоне, Древней Греции, Древней Индии и Китае, странах ислама; в эпоху Возрождения, эпоху Просвещения, в 19 и 20 веке)» (подбор материала, написание и оформление заключения, подготовка к защите реферата).
Решение тригонометрических задач на применение основных формул тригонометрии, а также формул приведения, двойного и половинного аргумента, преобразования суммы в произведение и обратно, задач на доказательство тождеств, геометрическую интерпретацию комплексных чисел и действия над комплексными числами.
Тема 1.4. Функции, их свойства и графики
После изучения темы обучающийся должен
уметь:
вычислять значение функции по значению аргумента и наоборот при различных способах задания функции;
определять основные свойства числовых функций, иллюстрировать их на графиках;
строить графики функций и описывать по графику и по формуле поведение и свойства функции;
применять элементарные преобразования для построения графиков функций;
находить область определения простейших функций и использовать понятие функции для описания и анализа зависимостей величин;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;
знать:
определение числовой функции, способы ее задания;
понятия области определения функции и множества ее значений;
простейшие преобразования графиков функций;
основные свойства функций;
понятие сложной и обратной функции;
свойства и графики изучаемых функций.
Функция, ее область определения и множество значений. Способы задания функции. График функции. Свойства функции: монотонность, четность (нечетность), ограниченность, периодичность. Промежутки возрастания и убывания, наибольшее и наименьшее значения. Примеры функциональных зависимостей в реальных процессах и явлениях. Обратная функция, ее график. Арифметические операции над функциями. Сложная функция (композиция). Линейная, дробно-линейная и квадратичная функции, их график и свойства. Асимптоты графика. Простейшие геометрические преобразования графика функции (параллельный перенос, симметрия, деформация).
Самостоятельная работа
Графическая работа «Элементарные преобразования графиков функций» (написание введения, построение в основной части базовых графиков функций и рассмотрение их параллельного переноса, деформации растяжения, сжатия и симметричного отображения, написание заключения).
Тема 1.5. Степенные, показательные, логарифмические и тригонометрические функции. Уравнения и неравенства
После изучения темы обучающийся должен
уметь:
строить графики изученных функций, в частности, применяя основные геометрические преобразования (параллельный перенос, симметрию и деформацию растяжения и сжатия);
описывать свойства изученных функций;
решать изученные виды уравнений, неравенств и их систем различными методами;
составлять и решать уравнения и неравенства, связывающие неизвестные величины в текстовых, прикладных задачах;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для построения и исследования простейших моделей;
знать:
Степенная функция с натуральным показателем, ее график и свойства. Решение целых и дробных рациональных уравнений и неравенств и их систем. Функция y=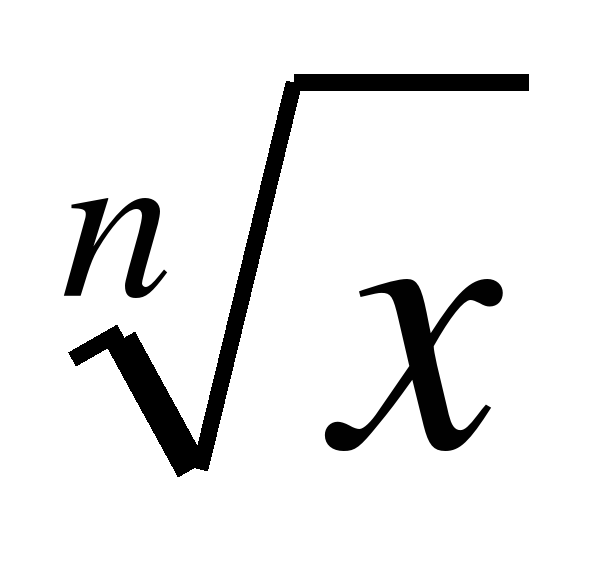 (n
(n N), ее график и свойства. Преобразования графиков: параллельный перенос; симметрия относительно осей координат, начала координат, прямой y = x; растяжение и сжатие вдоль осей координат. Равносильность уравнений, неравенств, их систем. Решение иррациональных уравнений и неравенств и их систем. Показательная функция, ее график и свойства. Решение показательных уравнений, неравенств и их систем. Логарифмическая функция, ее график и свойства. Решение логарифмических уравнений, неравенств и их систем. Тригонометрические функции y=sinx, y=cosx, y=tgx, y=ctgx, их свойства и графики. Арксинус, арккосинус, арктангенс числа. Обратные тригонометрические функции. Решение простейших тригонометрических уравнений по формулам и графически. Основные методы решения тригонометрических уравнений, неравенств и их систем (метод замены переменной, разложения на множители, графический метод и другие). Применение математических методов для решения содержательных задач из различных областей науки и практики.
N), ее график и свойства. Преобразования графиков: параллельный перенос; симметрия относительно осей координат, начала координат, прямой y = x; растяжение и сжатие вдоль осей координат. Равносильность уравнений, неравенств, их систем. Решение иррациональных уравнений и неравенств и их систем. Показательная функция, ее график и свойства. Решение показательных уравнений, неравенств и их систем. Логарифмическая функция, ее график и свойства. Решение логарифмических уравнений, неравенств и их систем. Тригонометрические функции y=sinx, y=cosx, y=tgx, y=ctgx, их свойства и графики. Арксинус, арккосинус, арктангенс числа. Обратные тригонометрические функции. Решение простейших тригонометрических уравнений по формулам и графически. Основные методы решения тригонометрических уравнений, неравенств и их систем (метод замены переменной, разложения на множители, графический метод и другие). Применение математических методов для решения содержательных задач из различных областей науки и практики.
Самостоятельная работа
Реферат с элементами исследования «Основные виды алгебраических (иррациональных, показательных, логарифмических, тригонометрических) уравнений и неравенств, методы их решения» (подбор теоретического материала, написание и оформление введения, подбор и изучение литературы, подбор материалов из Интернет – источников, написание и оформление первой, второй и третьей главы основной части, подбор материала, написание и оформление заключения, подготовка к защите).
Решение тригонометрических неравенств и логических задач.
Раздел 2. Начала математического анализа
Тема 2.1. Последовательности
После изучения темы обучающийся должен
уметь:
знать:
Числовые последовательности, способы их задания и свойства. Предел последовательности, теоремы о пределах. Существование предела монотонной ограниченной последовательности. Суммирование последовательностей. Бесконечно убывающая геометрическая прогрессия, ее сумма. Предел функции в точке и на бесконечности. Понятие о непрерывности функции.
Самостоятельная работа
Решение задач о прогрессиях, на вычисление пределов последовательностей и функций в точке и на бесконечности (в том числе, иррациональных и с помощью замечательных пределов), на отыскание точек разрыва и исследование функций на непрерывность.
Тема 2.2. Основы дифференциального исчисления
После изучения темы обучающийся должен
уметь:
находить производные элементарных функций;
использовать производную для изучения свойств функций и построения графиков;
решать прикладные социально-экономические, геометрические, физические задачи на нахождение наибольшего и наименьшего значения;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения прикладных задач, в том числе социально-экономических;
знать:
определение производной, ее геометрический и механический смысл;
правила и формулы дифференцирования;
уравнение касательной к графику функции в данной точке;
признаки монотонности, выпуклости (вогнутости) графика функции, алгоритмы исследования функции на экстремумы и перегибы;
общую схему анализа и построения графиков функции с помощью производной;
теорему о существовании наибольшего (наименьшего) значения функции и алгоритм исследования функции на наибольшее (наименьшее) значения на отрезке.
Понятие о производной функции, физический и геометрический смысл производной. Правило нахождения производной по четырем шагам. Уравнение касательной к графику функции. Производные суммы, разности, произведения и частного. Производные основных элементарных функций. Производные сложных функций. Производная обратной функции. Признаки монотонности функции. Исследование функции на экстремум с помощью производной. Вторая производная, ее геометрический и физический смысл. Признаки выпуклости, вогнутости графика функции. Точки перегиба. Применение производной к исследованию функций и построению графиков. Использование производных при решении уравнений и неравенств, текстовых, физических и геометрических задач, нахождении наибольших и наименьших значений. Решение задач на оптимальный вариант.
Самостоятельная работа
Реферат «Решение экономических задач с помощью производной и интеграла»: введение (подбор теоретического материала, написание и оформление введения); первая глава основной части (рассмотрение задач, приводящих к производной, изучение правила нахождения производной по четырем шагам и правил дифференцирования, выведение формул дифференцирования, оформление таблицы производных, подбор примеров на дифференцирование, написание и оформление первой главы); вторая глава основной части (углубленное изучение механического и геометрического смысла производной, методов исследования функции на монотонность и экстремумы (с подбором примеров), поиск теоретического материала для второй главы в литературе, поиск и составление задач на оптимизацию экономической направленности, решение задач экономической направленности с помощью производной, написание и оформление второй главы).
Тема 2.3. Основы интегрального исчисления
После изучения темы обучающийся должен
уметь:
находить неопределенные интегралы методом непосредственного интегрирования;
вычислять определенные интегралы;
вычислять в простейших случаях площади плоских фигур, объемы тел вращения и решать прикладные социально-экономические и физические задачи с помощью определенного интеграла;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения прикладных задач, в том числе социально-экономических;
знать:
определение первообразной, неопределенного и определенного интеграла;
формулы интегрирования, свойства интегралов;
приложения определенного интеграла к решению прикладных задач.
Понятие о первообразной функции и неопределенном интеграле. Формулы и правила интегрирования. Криволинейная трапеция и задача вычисления ее площади. Понятие об определенном интеграле. Формула Ньютона-Лейбница. Свойства определенного интеграла. Вычисление криволинейных фигур, объема тела вращения с помощью определенного интеграла. Решение физических, экономических задач с помощью определенного интеграла.
Самостоятельная работа
Реферат «Решение экономических задач с помощью производной и интеграла»: третья глава основной части (изучение основных понятий третьей главы, формул и свойств неопределенного интеграла с их доказательством, оформление таблицы интегралов, подбор примеров на интегрирование, нахождение неопределенных интегралов, изучение определенного интеграла и его экономического смысла, написание и оформление третьей главы); заключение (подбор материала, подведение итогов работы, написание и оформление заключения); подготовка к защите.
Раздел 3. Комбинаторика, статистика и теория вероятностей
Тема 3.1. Элементы комбинаторики
После изучения темы обучающийся должен
уметь:
знать:
Основные понятия комбинаторики. Задачи на перебор вариантов, на подсчет числа размещений, перестановок, сочетаний без повторений по соответствующим комбинаторным формулам. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля. Решение простейших комбинаторных уравнений.
Самостоятельная работа
Составление теста (задания на вычисления по комбинаторным формулам, свойства биномиальных коэффициентов, простейшие текстовые задачи по комбинаторике).
Тема 3.2. Элементы теории вероятностей
После изучения темы обучающийся должен
уметь:
вычислять в простейших случаях вероятности событий на основе подсчета числа исходов, применяя классическую формулу вероятности;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для оценки вероятностей случайных событий;
знать:
понятие события, классическое определение вероятности события;
теоремы о сложении и умножении вероятностей.
Случайные события. Классическое определение и формула вероятности события. Вероятность противоположного события. Вероятность суммы событий, несовместных событий. Вероятность произведения событий, независимых событий. Дискретная случайная величина, закон ее распределения. Числовые характеристики дискретной случайной величины. Понятие о законе больших чисел.
Самостоятельная работа
Составление теста (задания на вычисление вероятности случайного события, числовых характеристик случайной величины), проверка и оформление теста.
Решение задач на вычисление вероятности с помощью теорем суммы и произведения, задач о дискретной случайной величине.
Тема 3.3. Элементы математической статистики
После изучения темы обучающийся должен
уметь:
составлять выборочный ряд, статистическое распределение;
строить полигон частот выборки;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для анализа реальных числовых данных, представленных в виде диаграмм, графиков, для анализа информации статистического характера;
знать:
понятия генеральной и выборочной совокупности, варианты и ее частоты, объема и размаха выборки и ее репрезентативности;
способы представления статистических данных.
Статистические данные. Генеральная совокупность и выборка. Объем выборки, ее размах. Репрезентативность выборки. Выборочный ряд. Среднее арифметическое, мода и медиана. Табличное и графическое представление статистических данных (статистическое распределение, полигон частот). Понятие о задачах математической статистики.
Самостоятельная работа
Исследовательская работа «Обработка статистических данных, полученных в результате опроса» (написание введения, получение числовых данных путем опроса, и их статистическая обработка, написание основной части и заключения, подготовка к защите).
Раздел 4. Геометрия
Тема 4.1. Прямые и плоскости в пространстве
После изучения темы обучающийся должен
уметь:
описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения, делать чертеж к каждому случаю;
применять свойства параллельности и перпендикулярности прямых и плоскостей при решении задач;
вычислять углы и расстояния в пространстве;
осуществлять параллельное проектирование, изображать пространственные фигуры;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
знать:
основные понятия стереометрии;
аксиомы и первичные теоремы стереометрии;
случаи взаимного расположения двух прямых, прямой и плоскости, двух плоскостей в пространстве;
геометрические преобразования пространства: параллельный перенос, симметрию относительно плоскости.
Понятие об аксиоматическом способе построения геометрии. Основные понятия и аксиомы стереометрии. Случаи взаимного расположения двух прямых, прямой и плоскости, двух плоскостей в пространстве. Скрещивающиеся прямые, угол и расстояние между ними. Параллельность прямой и плоскости, ее признак, расстояние от прямой до плоскости. Перпендикулярность прямой и плоскости, ее признак. Перпендикуляр, наклонная к плоскости, проекция наклонной на плоскость. Расстояние от точки до плоскости. Угол между прямой и плоскостью. Теорема о трех перпендикулярах и ей обратная. Параллельность плоскостей, ее признак. Параллельные плоскости: их свойства, расстояние между ними. Перпендикулярность плоскостей, ее признак. Двугранный угол, его линейный угол и градусная мера. Геометрические преобразования пространства: параллельный перенос, симметрия относительно плоскости. Параллельное проектирование. Ортогональное проектирование, площадь ортогональной проекции. Изображение пространственных фигур.
Самостоятельная работа
Проект «Решение прикладных задач по стереометрии» (изучение аксиоматического способа построения и истории развития геометрии, аксиоматики стереометрии, параллельности и перпендикулярности в пространстве, написание и оформление введения).
Решение задач по теореме о трех перпендикулярах, задач о двугранном угле и о перпендикулярности плоскостей.
Тема 4.2. Многогранники
После изучения темы обучающийся должен
уметь:
соотносить изученные трехмерные объекты с их описаниями, чертежами, изображениями, различать и анализировать взаимное расположение пространственных фигур;
изображать призмы и пирамиды, выполнять пространственный чертеж по условию задачи;
решать геометрические задачи, опираясь на изученные свойства стереометрических фигур и отношений между ними, применяя алгебраический и тригонометрический аппарат;
проводить доказательные рассуждения при решении задач о призмах и пирамидах;
вычислять линейные элементы и углы в пространственных конфигурациях;
строить сечения призм и пирамид и находить площади сечений;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
знать:
понятие многогранника и правильного многогранника;
определения призмы, параллелепипеда, виды призм и их свойства;
определение пирамиды, правильной пирамиды.
Понятие многогранника, его вершины, ребра и грани. Развертка. Многогранные углы. Выпуклые многогранники. Теорема Эйлера. Призма. Прямая и наклонная призма. Правильная призма. Параллелепипед, его виды и свойства. Пирамида, ее грани и ребра, высота, апофема. Правильная пирамида. Усеченная пирамида. Тетраэдр. Понятие о симметрии в пространстве (центральной, осевой, зеркальной). Симметрии в кубе, параллелепипеде, призме, пирамиде. Сечения куба, призмы и пирамиды. Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр).
Самостоятельная работа
Проект «Решение прикладных задач по стереометрии» (изучение теоретического материала о многогранниках, призме, пирамиде и их частных случаях, выполнение чертежей, подбор, составление и решение прикладных задач о призме, пирамиде и их частных случаях, написание и оформление первой главы основной части).
Тема 4.3. Тела и поверхности вращения
После изучения темы обучающийся должен
уметь:
соотносить изученные трехмерные объекты с их описаниями, чертежами, изображениями, различать и анализировать взаимное расположение пространственных фигур;
изображать тела вращения, выполнять пространственный чертеж по условию задачи;
решать геометрические задачи, опираясь на изученные свойства стереометрических фигур и отношений между ними, применяя алгебраический и тригонометрический аппарат;
проводить доказательные рассуждения при решении задач о телах вращения;
вычислять линейные элементы и углы в пространственных конфигурациях;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
знать:
понятие тела вращения и поверхности вращения;
описательные определения цилиндра, конуса;
определения сферы, шара, случаи взаимного расположения шара и плоскости.
Цилиндр и конус как тела вращения. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения, параллельные основанию. Шар и сфера, их сечения. Случаи взаимного расположения сферы и плоскости. Прямая и обратная теоремы о касательной плоскости к сфере.
Самостоятельная работа
Проект «Решение прикладных задач по стереометрии» (изучение теоретического материала о цилиндре, конусе, усеченном конусе, шаре, выполнение их чертежей, подбор, составление и решение прикладных задач об этих телах вращения, написание и оформление второй главы основной части).
Тема 4.4. Измерения в геометрии
После изучения темы обучающийся должен
уметь:
вычислять объемы и площади поверхностей изученных многогранников и тел вращения;
применять отношения площадей поверхностей и объемов подобных тел при решении задач;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для вычисления объемов и площадей поверхностей пространственных тел при решении практических задач с использованием при необходимости справочных пособий и вычислительных средств;
знать:
понятие объема геометрического тела, теоремы и формулы объемов изученных многогранников и тел вращения;
теоремы и формулы для вычисления площадей поверхностей прямой призмы, правильной пирамиды, цилиндра, конуса и шара;
отношения площадей поверхностей и объемов подобных тел.
Объем и его измерение. Формулы объема призмы, параллелепипеда, куба, пирамиды. Вывод формул объема цилиндра, конуса с помощью определенного интеграла. Объем шара. Площадь поверхности пространственного тела. Теоремы о площади поверхности прямой призмы, правильной пирамиды. Вывод формул площадей поверхностей цилиндра и конуса. Площадь сферы. Подобие тел в пространстве. Отношения площадей поверхностей и объемов подобных тел.
Самостоятельная работа
Проект «Решение прикладных задач по стереометрии» (изучение теоретического материала об измерениях в стереометрии, подбор, составление и решение задач на вычисление объемов изученных тел, вычисление площадей поверхности призмы, пирамиды, усеченной пирамиды, изученных тел вращения, написание и оформление третьей главы основной части).
Решение задач на вычисление объемов призмы и ее частных случаев, пирамиды, усеченной пирамиды, цилиндра, конуса, усеченного конуса.
Тема 4.5. Координаты и векторы
После изучения темы обучающийся должен
уметь:
применять координатно-векторный метод для вычисления отношений, расстояний и углов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для исследования (моделирования) несложных практических ситуаций с помощью координатно-векторного метода;
знать:
прямоугольную декартову систему координат в пространстве;
формулу расстояния между двумя точками пространства;
действия над векторами в пространстве, формулу вычисления угла между ними;
понятие о компланарных векторах, разложение вектора по трем некомпланарным векторам;
Прямоугольная (декартова) система координат в пространстве. Формула расстояния между двумя точками. Уравнения сферы, плоскости и прямой. Векторы. Модуль вектора. Равенство векторов. Сложение векторов и умножение вектора на число. Коллинеарность векторов. Разложение вектора по направлениям. Угол между векторами. Проекция вектора на ось. Координаты вектора. Вычисление длины вектора. Скалярное произведение векторов. Вычисление угла между векторами. Использование координат векторов при решении математических и прикладных задач.
Самостоятельная работа
Проект «Решение прикладных задач по стереометрии» (подбор материала для написания заключения, написание и оформление заключения, подготовка электронной презентации, подготовка к защите проекта).
Решение задач на скалярное произведение векторов.
4. Перечень литературы
Алимов, Ш.А. и др. Алгебра и начала анализа: учеб. для 10 - 11 кл. общеобразоват. учреждений. – 15-е изд. – М.: Просвещение, 2007. – 384, с.
Атанасян, Л.С. и др. Геометрия, 10 - 11: учеб. для общеобразоват. учреждений. – 15-е изд., доп. - М.: Просвещение, 2006. – 256, с.
Богомолов, Н.В. Практические занятия по математике: учеб. пособие для средних спец. учеб. заведений, 7-е изд., стер. – М.: Высшая школа, 2004. – 495, с.
Пехлецкий, И.Д. Математика: учебник для средних специальных учебных заведений. – М.: Academia, 2010. – 304, с.
Погорелов, А.В. Геометрия: учеб. для 10 – 11 кл. общеобразоват. учреждений. – 5-е изд. – М.: Просвещение, 2005. – 128, с.
Интернет-ресурсы
www.interneturok.ru
www.urokimatematiki.ru
5. Средства обучения
Таблицы, плакаты, схемы.
Раздаточные конспекты.
Чертежные принадлежности.
Макеты геометрических фигур.
Научные калькуляторы.
Компьютеры.
Проектор.
Интерактивная доска.
Учебные видеофильмы на DVD-носителях.
Столы.
Стулья.
19

 Получите свидетельство
Получите свидетельство Вход
Вход












 Рабочая программа по математике для специальности СПО "Экономика и бухгалтерский учет" (0.22 MB)
Рабочая программа по математике для специальности СПО "Экономика и бухгалтерский учет" (0.22 MB)
 0
0 544
544 13
13 Нравится
0
Нравится
0



