Рабочая тетрадь для заочного отделения

Государственное бюджетное профессиональное образовательное учреждение Краснодарского края

«Славянский сельскохозяйственный техникум»

ГБПОУ КК ССХТ

Мир неживой природы – это мир симметрии, придающий его творениям устойчивость и красоту.  Мир живой природы – это мир гармонии, в которой действует «Закон золотого сечения».

Тихий шелест листьев оценивается в 1 бел. Громкость шума, выраженная в белах, равна десятичному логарифму его физической силы.

Рабочая тетрадь

с методическими указаниями

для выполнения практических работ

ЕН.01 Математика

Специальности: 35.02.07 Механизация сельского хозяйства

г. Славянск-на-Кубани, 2017

Печатается по решению редакционно-издательского совета ГБПОУ КК ССХТ

Рецензенты:

Гриценко Г.В. – преподаватель математики, заместитель директора филиала НОУ ВПО «МПСУ» в ст. Полтавская Краснодарского края;

Ковалева М.Г. – учитель математики МАОУ СОШ №17.

Рабочая тетрадь с методическими указаниями для выполнения практических работ: ЕН.01 Математика/ Автор-составитель Г.В. Занина – Славянск-на-Кубани: ГБПОУ КК ССХТ, 2017. – 47 c.

Рабочая тетрадь представляет собой готовый дидактический материал для проведения практических работ по ЕН.01 Математика. Пособие адресовано преподавателям и студентам специальности 35.02.07 Механизация сельского хозяйства сельскохозяйственной продукции ГБПОУ КК ССХТ.

Рабочая тетрадь

с методическими указаниями

для выполнения практических работ

ЕН.01 Математика

Специальности: 35.02.07 Механизация сельского хозяйства

Ф.И.О.____________________________________

__________________________________________

[специальность, группа]

В курсе учебной дисциплины «Математика» предусмотрены практические работы. Они предназначены для закрепления изученного материала, а также для проведения тематического контроля. Рабочая тетрадь поможет преподавателю и студенту в организации самостоятельной работы как на уроке (с отдельными студентами, группой студентов или всей группой), так и дома. Материал тетради расположен в соответствии с логикой изложения курса в учебной программе и дисциплине «Математика». В тетради с разнообразными тренировочными заданиями представлены нестандартные упражнения, вызывающие интерес и способствуют развитию наблюдательности, памяти, воображения, логического мышления, моторики, развитию счетных умений, формированию умений анализировать и решать задачи, развитию чертежных навыков. Печатная основа тетради позволяет значительно сократить время на выполнение заданий. Совместное использование лекционной части и рабочей тетради способствует рационализации учебного процесса.

№п\р
оценка

Уважаемые студенты!

«Математика имеет задачей

не обучение счислению, но обучения

приема человеческой мысли при исчислении».

Рабочая тетрадь по дисциплине «Математика» содержит набор практических работ для студентов 2 курса по специальности 35.02.07 Механизация сельского хозяйства и предназначена для системной работы.

Рабочая тетрадь предусматривает достижение двух целей:

а) довести изучение материала до уровня, на котором студенту становится ясна его принципиальная математическая значимость, до известной степени завершенности;

б) показать непосредственные выходы математики в сферы профессиональной науки и ее приложений. В рабочей тетради представлена история возникновения и развития ряда изучаемых методов, концепций и идей, их значение для математики и других наук и областей практической деятельности.

Весьма существенное место в рабочей тетради занимает решение задач и упражнений. При этом среди них находится весьма значительное число традиционных задач. Помимо этого, рабочая тетрадь предусматривает обязательное выделение времени для решения задач повышенной трудности по общему курсу математики.

Систематическая работа в рабочей тетради приводит к метапредметным результатам, т. е. применение деятельности, как в рамках образовательного процесса, так и при решении проблем реальных жизненных ситуаций. В тетради имеется таблица для устного счета с отметкой о правильности сделанной работы. В рабочую тетрадь включены разноуровневые, творческие, исследовательские и проектные задания. Имеются два вида высказываний: выражения для создания успешной ситуации и умные, мудрые мысли о математике.

В ней вы найдёте тесты контрольных вопросов и проверочные задания к каждой практической работе. Их цель – не только закрепить полученные знания, но и проверить усвоение предметных знаний и умений по каждой крупной теме курса на необходимом уровне.

Работая над имеющимися в тетради заданиями, вы сможете самостоятельно проверить свои знания и практические умения при решении задач разных тема так же просмотреть выполненные задания, готовясь к зачёту или к экзамену. В каждой практической работе дано краткое описание тем и разделов учебной дисциплины, её цели и задачи в подготовке специалистов.

Практическая работа №1

Раздел: Основные понятия и методы математического анализа.

Тема: Основы дифференциального исчисления.

Наименование работы: Вычисление пределов функций.

Метод, способ проведения: Самостоятельная работа студентов под руководством преподавателя.

Организация работы: Фронтальный опрос, комментированное решение у доски.

Цель занятия: Научиться вычислять пределы функций.

Умения и навыки: Уметь вычислять пределы простейших функций.

Оснащения рабочего места: Доска, конспект, рабочая тетрадь.

Литература:

Гусев, В. А. Математика для профессий и специальностей социально- экономического профиля: учебник для образовательных учреждений нач. и сред. проф. образования /В.А. Гусев, С. Г. Григорьев, С. В. Иволгина. – 2-е изд., стер. – М: Издательский центр «Академия», 2011, стр. 168-177

Вычислите устно и результаты запишите в таблицу:

1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	Всего правильно

Думайте, действуйте и говорите с энтузиазмом, и вы притяните позитивные результаты. Михаил ЛеБеф

Контрольные вопросы при допуске к работе:

1) Что называется пределом функции при х→х˳?

____________________________________________________________________________________________________________________________________________________________________________________________________________

2) Что называется пределом функции при х→∞?

____________________________________________________________________________________________________________________________________________________________________________________________________________

________________________________________________________________________________________________________________________________________

3) Правила вычисления пределов функции. Два замечательных предела.

____________________________________________________________________________________________________________________________________________________________________________________________________________

________________________________________________________________________________________________________________________________________

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Содержание и последовательность выполнения работы.

Задание 1. Найти пределы функций:

1)

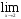
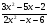
2)

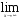
3)

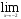
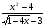
4)

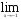
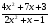
5)

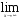
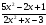
6)

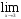
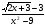
7)

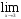
8)

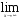
9)

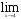
10)

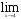
11)

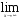
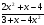
12)

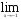
13)

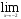
14)

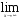
15)

16)

17)

18)

19)

20)

Домашнее задание:

1) А. Н. Колмогоров « Алгебра начала анализа» стр. 121 (№230, 226)

2) Реферат на тему: «Раскрытие неопределенностей »,

« Решение пределов на 1-й и 2-й замечательные пределы».

3) Пользуясь определениями основных свойств функций, соотнесите предложенные пословицы к графикам функций.

Любишь кататься - люби и саночки возить.

Как аукнется - так и откликнется.

Чем дальше в лес, тем больше дров.

Повторенье – мать ученья. Предложите свои.

Например, пословица: "Выше меры конь не скачет". Если изобразить траекторию скачущего коня графически, то высота скачков в полном соответствии с пословицей будет ограничена сверху некоторой "мерой". Это свойство присуще функциям sin x и cos x. Здесь тоже своя "мера", за пределы которой не вздымаются волны синусоиды и косинусоиды.

Например, пословица "Пересев хуже недосева". Известно, что урожай лишь до некоторой поры растет вместе с плотностью посева, дальше он снижается, потому что при чрезмерной густоте ростки начинают глушить друг друга. Если эту характерность изобразить графически, где урожай представлен как функция плотности посева, то урожай максимален, когда поле засеяно в меру. Или максимум - это как бы вершина горы, с которой все дороги ведут только вниз, куда ни шагни, а минимум - как бы впадина, из которой куда ни шагни - все дороги ведут только вверх.

Ни одно человеческое исследования не может называться истиной наукой, если оно не прошло через математические доказательства.

Леонардо да Винчи.

Оценка­­­­­­­­­­­­­______________ __________________________

( Подпись преподавателя)

Практическая работа №2

Раздел: Основные понятия и методы математического анализа.

Тема: Основы дифференциального исчисления.

Наименование работы: Вычисление производной функции.

Метод, способ проведения: Самостоятельная работа студентов под руководством преподавателя.

Организация работы: Фронтальный опрос, комментированное решение у доски.

Цель занятия: Научиться выполнять производные функции, сложной функции.

Умения и навыки: Уметь выполнять производные элементарных функций и сложных функций.

Оснащение рабочего места: Доска, конспект, инструкционная карты.

Литература:

Гусев, В. А. Математика для профессий и специальностей социально- экономического профиля: учебник для образовательных учреждений нач. и сред. проф. образования /В.А. Гусев, С. Г. Григорьев, С. В. Иволгина. – 2-е изд., стер. – М: Издательский центр «Академия», 2011, стр. 168-177

Вычислите устно и результаты запишите в таблицу:

1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	Всего правильно

Математика — это искусство называть разные вещи одним и тем же именем.

А. Пуанкаре

Контрольные вопросы при допуске к работе:

1) Операция нахождения производной называется _________________________________________________________________

2) Напишите формулы дифференцирования элементарных функций ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________3) Какой физический смысл производной?

________________________________________________________________________________________________________________________________________

4) Перечислите свойства дифференциала функцию ____________________________________________________________________5) Как находить производную сложной функции___________________________

____________________________________________________________________

1. Производная суммы или разности
2. Производная произведения
2a. Производная выражения, умноженного на постоянный множитель
3. Производная частного
4. Производная сложной функции

Содержание и последовательность выполнения работы.

Задание 1. Найдите ошибку и исправь:

Задание 2. Найдите дифференциалы функции:

а)

б)

в)

_г)

Задание 3. Найти производные функций:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11) а)

₁₂)

13)

14)

15)

16) а)

Домашнее задание:

1. Составьте кроссворд, используя основные понятия данной темы.

2. Решите задачи: Оборудование производителя №1 изнашивается по закону:

s= 1/3t³+t²+2 оборудование производителя №2 s= 1/3t^3-t+5. Выберите производителя, скорость износа оборудования которого за период в 10 лет будет наименьшей и покажите графически траекторию износа его.

В математике есть своя красота, как в живописи и поэзии.

Н.Е. Жуковский

Оценка­­­­­­­­­­­­­______________ __________________________

( Подпись преподавателя)

Практическая работа №3

Раздел: Основные понятия и методы математического анализа.

Тема: Основы дифференциального исчисления.

Наименование работы: Приложение производной.

Метод, способ проведения: Самостоятельная работа студентов под руководством преподавателя.

Организация работы: Фронтальный опрос, комментированное решение у доски.

Цель занятия: Научиться находить производные различных функций, решать задачи на приложение производной функции.

Умения и навыки: Уметь находить экстремумы функций, исследовать графики функции с помощью производной.

Оснащение рабочего места: Доска, конспект, инструкционная карты.

Литература:

Гусев, В. А. Математика для профессий и специальностей социально- экономического профиля: учебник для образовательных учреждений нач. и сред. проф. образования /В.А. Гусев, С. Г. Григорьев, С. В. Иволгина. – 2-е изд., стер. – М: Издательский центр «Академия», 2011, стр. 168-177

Вычислите устно и результаты запишите в таблицу:

1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	Всего правильно

Скажи мне, и я забуду, покажи мне, и я запомню,

Дай мне действовать самому, и я научусь.

Древнекитайская мудрость.

Контрольные вопросы при допуске к работе:

Для полного исследования функции и построения ее графика рекомендуется следующая схема:
а) найти область определения, точки разрыва…..

____________________________________________________________________

б) определить четность или нечетность функции и сделать вывод …

____________________________________________________________________
в) найти точки пересечения функции с осями координат OY и OX (если это возможно) …________________________________________________________

____________________________________________________________________

г) найти первую производную  функции…______________________________

____________________________________________________________________

д) найти вторую производную  точках…_________________________________

____________________________________________________________________

е) найти наклонные (горизонтальные) асимптоты…._______________________

____________________________________________________________________
ж) найти дополнительные точки для уточнения графика ___________________

Содержание и последовательность выполнения работы.

Задание 1. Найти экстремумы функции: а)

_б)

Задания 2. Найти значение функции в точке максимума: а)

Задание 3. Найти значение производной функции f(x)=-3x³+2x²+4 в точке х=1.

Задание 4. Найдите наименьшее значение функции на законном отрезке.

_{Задание 5}. Вычислить значение производной при заданном значении аргумента.

Домашнее задание:

1) А. Н. Колмогоров стр.143-151(№281, 282).

2) Создайте свой опорный конспект по теме «Производные функции».

Математика выявляет порядок, симметрию и определенность, а это важнейшие виды прекрасного. Аристотель

Оценка­­­­­­­­­­­­­______________ __________________________

( Подпись преподавателя)

Практическая работа №4

Раздел: Основные понятия и методы математического анализа.

Тема: Основы дифференциального исчисления.

Наименование работы: Определение сходимости ряда.

Метод, способ проведения: Самостоятельная работа студентов под руководством преподавателя.

Организация работы: Фронтальный опрос, комментированное решение у доски.

Цель занятия: Научиться определять сходимость ряда, применяя признаки сходимости рядов и признак Даламбера.

Умения и навыки: Уметь определять сходимость ряда.

Оснащение рабочего места: Доска, конспект, рабочая тетрадь, раздаточный материал.

Литература:

Гусев, В. А. Математика для профессий и специальностей социально- экономического профиля: учебник для образовательных учреждений нач. и сред. проф. образования /В.А. Гусев, С. Г. Григорьев, С. В. Иволгина. – 2-е изд., стер. – М: Издательский центр «Академия», 2011, стр. 197-199

Вычислите устно и результаты запишите в таблицу:

1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	Всего правильно

Численные вычисления вам каждый день, поэтому методы их производства и должны быть усвоены в первую очередь. А.Н. Крылов

Контрольные вопросы при допуске к работе:

1) Что называют рядом?

____________________________________________________________________________________________________________________________________________________________________________________________________________

2) 2 признака сходимости рядов? ______________________________________

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

3) Приведите пример расходящегося ряда ________________________________

____________________________________________________________________

4) Приведите пример сходящегося ряда__________________________________

5) В чем заключается признак Даламбера_________________________________

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Содержание и последовательность выполнения работы.

Задание 1. Написать три первых члена степенного ряда по заданному общему члену . Найти интервал сходимости и исследовать сходимость ряда на концах этого интервала.

1) ; 2) ; 3) ; 4) ;

5) ; 6) ; 7) ; 8) ;

9) ; 10) .

Задания 2. Исследовать сходимость ряда по признаку Даламбера

1)

2)

3)

Домашнее задание:

1) Создайте свой опорный конспект по теме «Ряды».

Математика выявляет порядок, симметрию и определенность, а это важнейшие виды прекрасного. Аристотель

Оценка­­­­­­­­­­­­­______________ __________________________

( Подпись преподавателя)

Практическая работа №5

Раздел: Основные понятия и методы математического анализа.

Тема: Основы интегрального исчисления.

Наименование работы: Вычисление интегралов.

Метод, способ проведения: Самостоятельная работа студентов под руководством преподавателя.

Организация работы: Фронтальный опрос, комментированное решение у доски.

Цель занятия: Научиться вычислять неопределенные и определенные интегралы, применяя таблицу интегралов и теорему Ньютона – Лейбница.

Умения и навыки: Уметь вычислять интегралы, применяя свойства интегралов.

Оснащение рабочего места: Доска, конспект, рабочая тетрадь, раздаточный материал.

Литература:

Гусев, В. А. Математика для профессий и специальностей социально- экономического профиля: учебник для образовательных учреждений нач. и сред. проф. образования /В.А. Гусев, С. Г. Григорьев, С. В. Иволгина. – 2-е изд., стер. – М: Издательский центр «Академия», 2011, стр. 197-199

Вычислите устно и результаты запишите в таблицу:

1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	Всего правильно

Золото добывают из земли, а знания – из книги.

Контрольные вопросы при допуске к работе:

1) Что называют определенным интегралом?

____________________________________________________________________________________________________________________________________________________________________________________________________________

2) Сформулируйте свойства интегралов.

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________3) Описать суть метода подстановки в определенном интеграле.

________________________________________________________________________________________________________________________________________4) Формула Ньютона – Лейбница

________________________________________________________________________________________________________________________________________5)Задача, приводящая к понятию определенного интеграла заключается в следующем.._____________________________________________________________________________________________________________________________

Содержание и последовательность выполнения работы:

Задание 1. Вычислите определенный интеграл методом непосредственного интегрирования:

а)

б)

в)

г)

Задание 2. Вычислите определенные интегралы:

Задание 3. Вычислите неопределенные интегралы:

Домашнее задание: Выучите историю интегрального исчисления. Напишите доклад по теме: «Вычисление площадей и объемов»

В математических вопросах нельзя пренебрегать даже с самыми малыми ошибками. И. Ньютон

Оценка­­­­­­­­­­­­­______________ _______________________                                                                                                                    (Подпись преподавателя)

Практическая работа №6

Раздел: Основные понятия и методы математического анализа.

Тема: Основы интегрального исчисления.

Наименование работы: Приложение определенного интеграла.

Метод, способ проведения: Самостоятельная работа студентов под руководством преподавателя.

Организация работы: Фронтальный опрос, комментированное решение у доски.

Цель занятия: Научиться вычислять площади и объемы с помощью определенных интегралов, применяя теорему Ньютона – Лейбница.

Умения и навыки: Уметь вычислять площади и объемы.

Оснащение рабочего места: Доска, конспект, рабочая тетрадь, раздаточный материал.

Литература:

Гусев, В. А. Математика для профессий и специальностей социально- экономического профиля: учебник для образовательных учреждений нач. и сред. проф. образования /В.А. Гусев, С. Г. Григорьев, С. В. Иволгина. – 2-е изд., стер. – М: Издательский центр «Академия», 2011, стр. 189-194

Вычислите устно и результаты запишите в таблицу:

1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	Всего правильно

Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели. А. Маркушевич

Контрольные вопросы при допуске к работе:

1)Формула Ньютона – Лейбница______________________________________

2)Формулы вычисления площадей плоских фигур_________________________

___________________________________________________________________

3)Формулы вычисления объемов_______________________________________

Содержание и последовательность выполнения работы:

Задание 1. Найдите площадь фигуры, ограниченной линиями:

а)

б)

в)

г)

д)

Домашнее задание:

1. Найти площадь фигуры, ограниченной линиями.

2. Тема реферата «Применение интегрального исчисления в физике».

Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе. М.И. Калинин

Оценка­­­­­­­­­­­­­______________ __________________________

( Подпись преподавателя)

Практическая работа №7

Раздел: Основные понятия и методы математического анализа.

Тема: Обыкновенные дифференциальные уравнения.

Наименование работы: Решение дифференциальных уравнений.

Метод, способ проведения: Самостоятельная работа студентов под руководством преподавателя.

Организация работы: Фронтальный опрос, комментированное решение у доски.

Цель занятия: Научиться решать обыкновенные дифференциальные уравнения.

Умения и навыки: Уметь вычислять обыкновенные дифференциальные уравнения.

Оснащение рабочего места: Доска, конспект, рабочая тетрадь, раздаточный материал.

Литература:

Гусев, В. А. Математика для профессий и специальностей социально- экономического профиля: учебник для образовательных учреждений нач. и сред. проф. образования /В.А. Гусев, С. Г. Григорьев, С. В. Иволгина. – 2-е изд., стер. – М: Издательский центр «Академия», 2011, стр. 189-194

Вычислите устно и результаты запишите в таблицу:

1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	Всего правильно

«Главная жизненная задача человека – дать жизнь самому себе, стать тем, чем он является потенциально. Самый важный плод его усилий – его собственная личность» Э. Фромм

Контрольные вопросы при допуске к работе:

1) Задача приводящая к дифференциальному уравнению____________________

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

2) Дифференциальным уравнением называется …_________________________

____________________________________________________________________

________________________________________________________________________________________________________________________________________

3) Когда уравнение называется обыкновенным дифференциальным уравнением?

________________________________________________________________________________________________________________________________________

4) Приведите примеры дифференциальных уравнений разного порядка…

____________________________________________________________________________________________________________________________________________________________________________________________________________

Содержание и последовательность выполнения работы:

Задание 1. Решить уравнения: xdy=ydx, при х=5, у=10.

Задание 2. Решить уравнения: xdy=ydx, при х=6, у=24.

Задание 3. Решить уравнения: xdy=ydx, при х=4, у=16.

Задание 4. Решить уравнения: xdy=ydx, при х=5, у=20.

Задание 5. Решить уравнения: dy\dx=2(y-3), при х=0, у=4.

Задание 6. Решить уравнения: x*y*y'-3=0.

Домашнее задание:

1. Найти площадь фигуры, ограниченной линиями.

2. Тема реферата «Применение интегрального исчисления в физике».

Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе. М.И. Калинин

Оценка­­­­­­­­­­­­­______________ __________________________

( Подпись преподавателя)

Практическая работа №8

Раздел: Основные понятия и методы математического анализа.

Тема: Обыкновенные дифференциальные уравнения.

Наименование работы: Численное интегрирование и дифференцирование.

Метод, способ проведения: Самостоятельная работа студентов под руководством преподавателя.

Организация работы: Фронтальный опрос, комментированное решение у доски.

Цель занятия: Научиться решать обыкновенные дифференциальные уравнения, научиться численно численному интегрированию и дифференцированию.

Умения и навыки: Уметь вычислять обыкновенные дифференциальные уравнения, численно интегрировать и дифференцировать.

Оснащение рабочего места: Доска, конспект, рабочая тетрадь, раздаточный материал.

Литература:

Гусев, В. А. Математика для профессий и специальностей социально- экономического профиля: учебник для образовательных учреждений нач. и сред. проф. образования /В.А. Гусев, С. Г. Григорьев, С. В. Иволгина. – 2-е изд., стер. – М: Издательский центр «Академия», 2011, стр. 189-194

Вычислите устно и результаты запишите в таблицу:

1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	Всего правильно

Смотри на каждую утреннюю зарю, как на начало новой жизни, на каждый закат солнца, как на конец ее. Пусть каждая из этих кратких жизней будет отмечена каким-нибудь добрым поступком, какой-нибудь победой над собой или приобретенным знанием.

Д. Раскин

Контрольные вопросы при допуске к работе:

1) Задачи, приводящие к дифференциальному уравнению___________________

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

2) Дифференциальным уравнением называется …_________________________

____________________________________________________________________

________________________________________________________________________________________________________________________________________

3) Решение дифференциальных уравнений 1-го порядка____________________

4) Уравнения 2-го порядка: однородные и неоднородные___________________

5) Приведите примеры дифференциальных уравнений разного порядка…

Содержание и последовательность выполнения работы:

Задание 1. Найти общее решение дифференциального уравнения и частное его решение, удовлетворяющее начальному условию xdy=ydx, при х=15, у=75.

Задание 2. Найти общее решение дифференциального уравнения и частное его решение, удовлетворяющее начальному условию при .

; .

Задание 3. Найти общее решение дифференциального уравнения y'+2x*y=0.

Задание 4. Найти общее решение дифференциального уравнения y'+2(x+1)*у=0.

Задание 5 . Найти общее решение дифференциального уравнения y'+3у\x=2\х³

Домашнее задание:

1. Найти общее решение дифференциального уравнения и частное его решение, удовлетворяющее начальному условию при .

1) ; . 2) ; .

3)) ; .

2. Найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами. 1)

Есть в математике нечто, вызывающее человеческий восторг.

Ф. Хаусдорф

Оценка­­­­­­­­­­­­­______________ __________________________

( Подпись преподавателя)

Практическая работа №9

Раздел: Основные понятия и методы теории вероятностей и математической статистики.

Тема: Элементы теории вероятностей.

Наименование работы: Дискретная случайная величина и ее закон распределения.

Метод, способ проведения: Самостоятельная работа студентов под руководством преподавателя.

Организация работы: Фронтальный опрос, комментированное решение у доски.

Цель занятия: Научиться вычислять дискретные случайные величины, математическое ожидание, дисперсию, среднее квадратическое отклонение, научиться находить перестановки, вероятности случайных величин.

Умения и навыки: Уметь вычислять площади и объемы.

Оснащение рабочего места: Доска, конспект, рабочая тетрадь, раздаточный материал.

Литература:

Гусев, В. А. Математика для профессий и специальностей социально- экономического профиля: учебник для образовательных учреждений нач. и сред. проф. образования /В.А. Гусев, С. Г. Григорьев, С. В. Иволгина. – 2-е изд., стер. – М: Издательский центр «Академия», 2011, стр. 189-194

Вычислите устно и результаты запишите в таблицу:

1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	Всего правильно

Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели. А. Маркушевич

Контрольные вопросы при допуске к работе:

Термин «факториал» происходит от латинского слова factor – производящий. Произведение первых n натуральных чисел, т.е. 1• 2 • 3 •…• n

называют ____________________и обозначают n! n!= ..

Например, 4! = Функция n! возрастает очень быстро:

3! = ; 6!= . Факториалы в комбинаторике возникают очень часто. Поэтому принято считать, что если ответ выражен через факториал, то задача решена. Главное свойство факториала следует из определения: (n+1)!=(n+1)•n! Подставим в эту формулу n=0. Получим: 1!=1•0!, откуда 0!=1 Обозначением 0!=1 удобно пользоваться во многих формулах.

Содержание и последовательность выполнения работы.

Задание 1. Вычислить: а) б) в) г) д) е) ж)

Задание 2. Решите уравнения:

а) ;

б) ;

в) ;

г)

Задание 3. Решите систему уравнений:

Задание 4. Упростить: а)

б)

в)

г)

Задание 5. В ящике лежат 15 красных, 9 синих и 6 зеленых шаров, одинаковых на ощупь. Наудачу вынимают 1 (6) шаров. Какова вероятность того, что вынутый 1 зеленый, 2 синих и 3 красных шара.

Задание 6: Решите по вариантам предложенные задачи:

1. На столе 12 кусков пирога. В трех «счастливых» из них запечены призы. Какова вероятность взять «счастливый» кусок пирога?	1. В коробке 24 карандаша, из них 3 красного цвета. Из коробки наугад вынимается карандаш. Какова вероятность того, что он красный?
2. В урне 15 белых и 25 черных шаров. Из урны наугад выбирается один шар. Какова вероятность того, что он будет белым?	2. Из чисел от 1 до 25 наудачу выбрано число. Какова вероятность того, что оно окажется кратным 5?
3. За лето на Черноморском побережье было 67 солнечных дней. Какова частота солнечных дней на побережье за лето? Частота пасмурных дней?	3. Наблюдения показывают, что в среднем среди 1000 новорожденных детей 515 мальчиков. Какова частота рождения мальчика в такой серии наблюдений?
4. Чтобы определить, как часто встречаются в лесопарке деревья разных пород, ребята провели следующие эксперименты. Каждый выбрал свою тропинку и по пути следования записывал породу каждого десятого дерева. Результаты были занесены в таблицу: Породы Сосна Дуб Береза Ель Осина Всего Число деревьев 315 217 123 67 35 757 Оцените вероятность того, что выбранное наугад в этом парке дерево будет: а) сосной; б) хвойным; в) лиственным. Указание. Ответ запишите в виде десятичной дроби с тремя знаками после запятой.	4. По статистике, на каждые 1000 лампочек приходится 3 бракованные. Какова вероятность купить исправную лампочку? Как и почему возникла теория вероятностей?
5. Сколькими способами можно группу из 12 человек разбить на 2 подгруппы, в одной из которых должно быть не более 5, а во второй – не более 9 человек? Как и почему возникла теория вероятностей?	5. Имеется 10 белых и 5 черных шаров. Сколькими способами можно выбрать 7 шаров, чтобы среди них были 3 черных? 6. Нужно выбрать в подарок 4 из 10 имеющихся книг. Сколькими способами это можно сделать?

Задание 5. Найти: а) математическое ожидание М(Х); б) дисперсию Д(Х) – двумя способами; в) среднее квадратическое отклонение σ(Х), дискретной случайной величины Х по данному закону её распределения (в первой строчке указаны возможные значения х_i , во второй строке – вероятности возможных значений – р_i ).

хi	4	6	8	10	12
рi	0.2	0.3	0.1	0.2	0.2

хi	5	7	9	11	12
рi	0.2	0.3	0.1	0.2	0.2

хi	3	5	11	10	15
рi	0.2	0.3	0.6	0.2	0.6

Домашнее задание:

1. В лотерее выпущено 20 билетов, 10 из которых выигрывают. Куплено 5 билетов. Какова вероятность того, что, по крайней мере, один из купленных билетов выигрышный?

1. Вычислить:			2. Решить уравнения:
а) 6!; б) ;	в) ; г) ;	д) ; е) ;	а) ; б) .

Математика — это единственный совершенный метод водить самого себя за нос. Альберт Эйнштейн

Оценка­­­­­­­­­­­­­______________ __________________________

( Подпись преподавателя)

Практическая работа №10

Раздел: Основные понятия и методы теории вероятностей и математической статистики.

Тема: Элементы математической статистика.

Наименование работы: Нахождение основных характеристик вариационного ряда.

Метод, способ проведения: Самостоятельная работа студентов под руководством преподавателя.

Организация работы: Фронтальный опрос, комментированное решение у доски.

Цель занятия: Научиться вычислять дискретные случайные величины, научиться находить перестановки, вероятности случайных величин.

Умения и навыки: Уметь вычислять дискретные случайные величины, научиться находить перестановки, вероятности случайных величин.

Оснащение рабочего места: Доска, конспект, рабочая тетрадь, раздаточный материал.

Литература:

Гусев, В. А. Математика для профессий и специальностей социально- экономического профиля: учебник для образовательных учреждений нач. и сред. проф. образования /В.А. Гусев, С. Г. Григорьев, С. В. Иволгина. – 2-е изд., стер. – М: Издательский центр «Академия», 2011, стр. 189-194

Вычислите устно и результаты запишите в таблицу:

1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	Всего правильно

Золото добывают из земли, а знания – из книги.

Контрольные вопросы при допуске к работе:

Перестановками из множества n элементов называются всевозможные комбинации из этих n элементов, которые отличаются друг от друга только порядком расположения элементов. Число всех перестановок из n элементов обозначается Р_n (от французского слова permutation- перестановка).

Формула для отыскания числа перестановок из n элементов: Р_n=n!

Итак, перестановки – частный случай размещения, когда m=n:

Задача - притча: Старая английская легенда рассказывает, что некоторый хозяин таверны предложил своим 10 постоянным клиентам перепробовать все возможные варианты рассаживания за их обеденным столом и пообещал, что после того, как все различные варианты будут исчерпаны, он начнет кормить их бесплатно до конца их дней. Возможно ли это?

Пример: размещениями из 4-х элементов a b c d по 2 будут:a b; b a; ….

Содержание и последовательность выполнения работы:

Задание 1.

1. Из колоды в 36 карт вынимается одна. Какова вероятность появления карты червовой масти?

2. У нас есть 9 разных книг из серии «Занимательная математика». Сколькими способами можно расставить их на полке

3. Студенты колледжа изучают в каждом семестре по десять дисциплин. В расписание занятий включается каждый день по 3 дисциплины. Сколько различных расписаний можно составить диспетчерская?

Задание 2.

Случайная величина Х задана интегральной функцией F(x). Требуется: а) убедиться, что заданная функция F(x) является функцией распределения некоторой случайной величины, проверив свойства F(x). В случае положительного ответа найти: б) дифференциальную функцию (плотность распределения) f(x); в) математическое ожидание случайной величины Х; г) дисперсию случайной величины Х; д) среднее квадратическое отклонение; е) построить графики интегральной и дифференциальной функций (F(x) и f(x) соответственно); ж) определить вероятность попадания величины Х в интервал двумя способами (используя интегральную и дифференциальную функции), а затем проиллюстрировать этот результат на графиках F(x) и f(x):

задача	F(x)		
1		-3	0

Задание 1. Согласно номеру своего варианта сгруппировать хозяйства на три группы. По группировочному признаку составить ранжированный ряд.
Группировку выполнить в рабочей таблице.
Исходные данные для выполнения задания.
«Сводка и группировка статистических данных»

№ хозяйст ва	Урожайность зерновых культур ц/га	Площадь посева зерновых га	Валовой сбор зерновых ц	Урожайнос ть картофеля ц\га	Площадь посадки картофеля га		Валовой сбор, картофеля ц\га		Поголо вье скота гол		Средне- годовой надой на 1 корову кг		Валовой надой молока, ц
1	2	3	4	5	6		7		8		9		10
1	36	809	29124	Г22		280		34160		4022		3372		62685
2	29	705	20445	215		130		27950		6216		4630		117880
3	29	1067	30943	109		500		54500		4824		2909		76536
4	35	630	22050	136		200		27200		2979		4366		66931
5	43	632	27176	110		300		33000		4913		4213		31682
6	24	390	9360	90		94		8460		1390		3789		22734
7	32	1144	36608	94		264		24816		2369		3427		53907
8	43	600	25800	138		200		27600		3366		3690		54944
9	15	878	13170	140		220		30800'		2358		2795		23813
10	26	893	23218	75		180		13500		2042		2681		20483
И	29	850	24650	138		225		31050		5226		4200		28482
12	45	375	16875	160		245		39200		2591		3348		47106
13	23	490	11270	93		225		20925		2363		3069		43948
14	45	380	16340	169		255		43095		2791		3448		51720
15	31	740	22940	192		235		45120		3765		3053		60840

1 Вариант - по урожайности зерновых культур. По каждой группе и по всей совокупности в целом подсчитать: а)число хозяйств по группам; б)среднюю урожайность зерновых, ц/га; в) посевную площадь зерновых культур, га; г) валовой сбор зерновых культур, ц/га.	4 Вариант - по площади посадки картофеля. По каждой группе и по всей совокупности в целом подсчитать: а)число хозяйств по группам; б)площадь посадки картофеля, га; в)валовой сбор картофеля, ц; г)среднюю урожайность картофеля, ц/га.
2 Вариант - по площади посева зерновых культур. По каждой группе и по всей совокупности в целом подсчитать: а)число хозяйств по группам; б)площадь посева Зерновых, га; в)валовой сбор зерновых, ц; г)среднюю урожайность зерновых ц/га.	5 Вариант - по поголовью коров, по каждой группе и по всей совокупности в целом подсчитать; а)число хозяйств по группам; , б)поголовье коров, гол; в)валовой надой молока, ц; г)среднюю продуктивность коров, ц.
3 Вариант - по урожайности картофеля. По каждой группе и по всей совокупности в целом подсчитать: а)число хозяйств по группам; б)среднюю урожайность картофеля, ц/га;. в)площадь посадки картофеля, га; г)валовой сбор картофеля, ц.	6 Вариант - по продуктивности коров. По каждой группе и по всей совокупности в целом подсчитать: а)число хозяйств по группам; б)среднюю продуктивность коров, ц; в)поголовье коров, гол; г)валовой надой молока, ц.

4. По группировочному признаку составить ранжированный ряд.

Группировочный признак - ____________________________________________________________________
____________________________________________________________________
____________________________________________________________________

Ранжированный ряд:

	1	2	3	4	5	6	7	8	9	10	И	12	13	14	15
№ хозяйства
Размер группир. признака

2. Определить размер интервала:

3. Определить границы групп:

1 группа -

2 группа -

3 группа –

Распределить данные статистического наблюдения по группам согласно
группировочного признака (таблица 1).

Подсчитать итоги по каждой графе таблицы 1
Рабочая таблица

1 группа границ от________ до_________

2 группа границ от_________ до_________

3 группа границ от________ до_________

Порядко­вый № х-ва

Порядко­вый № х-ва

Порядко- - вый № х-ва

-

** Средняя урожайность сельскохозяйственных культур определяется делением суммы валового сбора на сумму площади посева

*** Средняя продуктивность коров определяется делением суммы валового надоя молока на поголовье коров

5. Подсчитать итоги группировочных показателей по всей используемой совокупности в среднем на 1 хозяйство:

а) 1 группа -

2 группа -

3 группа –

Итого:

б) 1 группа -

2 группа - в среднем на 1 хозяйство

3 группа -

Итого:

в) 1 группа -

2 группа - в среднем на 1 хозяйство

3 группа –

Итого:

г) 1 группа -

2 группа - в среднем на 1 хозяйство

3 группа –

Итого:

Домашнее задание:

1. Вычислить: а) ; б) =5040-120=4920; в) .

2. В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

Развитие математики вновь подтверждает, что деление наук на теоретическую часть и практическую неправильно. Наук едина, и можно говорить лишь о самой науке и её возможно приложения приложениях. Боголюбов Н.Н., Лаврентьев М.А.

Оценка­­­­­­­­­­­­­______________ __________________________ (Подпись преподавателя)

РАБОЧАЯ ТЕТРАДЬ

с методическими указаниями

для выполнения практических работ

ЕН.01 Математика

Специальности: 35.02.07 Механизация сельского хозяйства

Корректор: С.А. Семенова

Подписано в печать:__.__. 2017 г.

Печатьцифровая. Бум. Тип. № 2.Формат _____ 1/16

Тираж: 55 экз. Заказ №

Отпечатано в полиграфической лаборатории ГБПОУ КК ССХТ:

г. Славянск-на-Кубани, ул. Набережная, 8

Таблица интегралов