Рабочая программа
по учебному предмету «Математика»
в 11 «А» классе
(профильное обучение)
г
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Учебный план разработан на основе:
- Федерального закона от 29.12.2012 № 273-ФЗ «Об образовании в Российской Федерации»;
-приказа Министерства образования Российской Федерации от 09.03.2004 № 1312 «Об утверждении федерального базисного учебного плана и примерных планов для образовательных учреждений Российской Федерации, реализующих программы общего образования» (в ред. приказов Минобрнауки России от 20.08.2008 № 241, от 30.08.2010 № 889, от 03.06.2011 № 1994, от 01.02.2012 № 74);
приказа Министерства образования Российской Федерации от 05.03.2004 №1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования»;
приказа департамента образования, науки и молодежной политики Воронежской области от 27.07.2012 № 760 «Об утверждении регионального базисного учебного плана и примерных учебных планов для образовательных учреждений Воронежской области, реализующих государственные образовательные стандарты начального общего, основного общего и среднего (полного) общего образования»;
- приказа департамента образования, науки и молодежной политики Воронежской области от 30 августа 2013 №840 «О внесении изменения в приказ департамента образования, науки и молодежной политики Воронежской области от 27.07.2012 №760»;
- приказа Министерства образования и науки РФ от 31.03.2014 года № 253 «Об утверждении федерального перечня учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования»,
- постановления Главного государственного санитарного врача Российской Федерации от 29.12.2010 № 189 «Об утверждении СанПиН 2.4.2.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях» (зарегистрировано в Минюсте России 03.03.2011, регистрационный номер 19993);
- Концепции профильного обучения на старшей ступени общего образования, утвержденной приказом Министерства образования Российской Федерации от 18.07.2002 № 2783;
-Письма Министерства образования Российской Федерации от 20.04.2004 № 14-51-102/13 «О направлении Рекомендаций по организации профильного обучения на основе индивидуальных учебных планов обучающихся»;
- Программы введения предпрофильной подготовки и профильного обучения в образовательных учреждениях Воронежской области, утвержденной приказом главного управления образования администрации Воронежской области от 18.08.2004 № 547.
Количество недельных часов: 6 часов в неделю.
Количество часов в год: 204 часа.
Уровень рабочей программы: профильный
Классификация рабочей программы: авторская
Математическое образование вносит свой вклад в формирование общей культуры человека. Необходимым компонентом общей культуры в ее современном толковании является общее знакомство с методами познания действительности, что включает понимание диалектической взаимосвязи математики и действительности, представление о предмете и методе математики, его отличиях от методов естественных и гуманитарных наук, об особенностях применения математики для решения научных и прикладных задач.
В профильном курсе содержание образования, представленное в основной школе, развивается в следующих направлениях:
• систематизация сведений о числах; формирование представлений о расширении числовых множеств от натуральных до комплексных как способе построения нового математического аппарата для решения задач окружающего мира и внутренних задач математики; совершенствование техники вычислений;
• развитие и совершенствование техники алгебраических преобразований, решения уравнений, неравенств, систем;
• систематизация и расширение сведений о функциях, совершенствование графических умений; знакомство с основными идеями и методами математического анализа в объеме, позволяющем исследовать элементарные функции и решать простейшие
• развитие представлений о вероятностно-статистических закономерностях в окружающем мире;
• совершенствование математического развития до уровня, позволяющего свободно применять изученные факты и методы при решении задач из различных разделов курса, а также использовать их в нестандартных ситуациях;
• формирование способности строить и исследовать простейшие математические модели при решении прикладных задач, задач из смежных дисциплин, углубление знаний об особенностях применения математических методов к исследованию процессов и явлений в природе и обществе.
Изучение математики в старшей школе на профильном уровне направлено на достижение следующих целей:
формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов;
овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественно-научных дисциплин, для продолжения образования и освоения избранной специальности на современном уровне;
развитие логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности;
воспитание средствами математики культуры личности: знакомство с историей развития математики, эволюцией математических идей, понимание значимости математики для общественного прогресса.
совершенствование проведения доказательных рассуждений, логического обоснования выводов, использования различных языков математики для иллюстрации, интерпретации, аргументации и доказательства;
решение широкого класса задач из различных разделов курса, развитие поисковой и творческой деятельности при решении задач повышенной сложности и нетиповых задач;
планирование и осуществление алгоритмической деятельности: выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; использование самостоятельного составления формул на основе обобщения частных случаев и результатов эксперимента; выполнение расчетов практического характера;
построение и исследование математических моделей для описания и решения прикладных задач, задач из смежных дисциплин и реальной жизни; проверки и оценки результатов своей работы, соотнесения их с поставленной задачей, с личным жизненным опытом;
совершенствование самостоятельной работы с источниками информации, анализа, обобщения и систематизации полученной информации, интегрирования ее в личный опыт.
развитие представлений о вероятностно-статистических закономерностях в окружающем мире.
Реализацию вышеуказанных целей обеспечивают учебно-методические комплекты: «Алгебра и начала анализа 11 класс» авторы: С. М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин; «Геометрия. 10-11 классы» авторы: Атанасян Л.С, Бутузов В.Ф. и др.
Разрабатывая данную программу, я опирались именно на эти УМК.
Данная рабочая программа разработана на основе примерной программы по математике, рекомендованной Департаментом образовательных программ и стандартов общего образования МО РФ, «Программы общеобразовательных учреждений. Алгебра и начала анализа. 10-11 классы, - М.Просвещение, 2009. Авторы: М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. Составитель Т. А. Бурмистрова», «Программы общеобразовательных учреждений. Геометрия. 10-11 классы, - М.Просвещение, 2010. Авторы: Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др. (базовый и профильный уровни) Составитель Т. А. Бурмистрова».
Согласно Федерального базисного учебного плана на изучение математики на профильном уровне в 101классе отводится не менее 210 часов из расчета 6 ч в неделю.
Формы обучения и контроля: традиционные уроки, контрольная работа, самостоятельная работа, тестовая работа, практикум по решению задач, уроки с использованием ИКТ.
Виды и формы контроля:
Виды: текущий, периодический (тематический), итоговый, самоконтроль.
Формы контроля: устный и письменный, фронтальный и индивидуальный.
Учебно-методический комплект для обучающихся:
Алгебра и начала анализа: учебник для 11 класса общеобразовательных учреждений. Составители:. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. — М.: Просвещение, 20013.
«Алгебра и начала анализа. Дидактические материалы для 11 класса базовый и профильный уровни 3 –е издание, - М. Просвещение, 2015. Авторы: М. К. Потапов и А. В. Шевкин»
«Алгебра и начала математического анализа. Тематические тесты для 11 класса базовый и профильный уровни, - М. Просвещение, 2015. Автор Ю. В. Шепелева»
«Алгебра и начала математического анализа 11 класс. Книга для учителя. Базовый и профильный уровни, - М. Просвещение, 2015. Авторы: М. К. Потапов и А. В. Шевкин».
Геометрия, 10-11: Учебник для общеоб. учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Позняк, Л. С. Киселева - М.: Просвещение, 2014
Б.Г. Зив. Дидактические материалы по геометрии для 11 класса. – М. Просвещение, 20013 г
Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по алгебре для 11 класса.- 4-е издание, испр. и доп.- М.:Илекса, 2012,- 175 с.
Срок реализации рабочей учебной программы – один учебный год.
Учебно-тематический план
| № п/п | Наименование разделов и тем | Кол-во часов программы |
| 1. | Функции и их графики | 9 |
| 2. | Предел функции и непрерывность | 5 |
| 3. | Обратные функции | 6 |
| 4. | Производная | 11 |
| 5. | Применение производной | 16 |
| 6. | Первообразная и интеграл | 13 |
| 7. | Равносильность уравнений и неравенств | 4 |
| 8 | Уравнения-следствия | 8 |
| 9. | Равносильность уравнений и неравенств системам | 13 |
| 10. | Равносильность уравнений на множествах | 7 |
| 11. | Равносильность неравенств на множествах | 7 |
| 12. | Метод промежутков для уравнений и неравенств | 5 |
| 13. | Использование свойств функций при решении уравнений и неравенств . | 5 |
| 14. | Системы уравнений с несколькими неизвестными | 8 |
| 15. | Векторы в пространстве | 7 |
| 16. | Метод координат в пространстве | 15 |
| 17 | Цилиндр, конус и шар | 16 |
| 18 | Объемы тел | 16 |
| 19 | Повторение | 33 |
Контроль уровня обученности обучающихся
| № п/п | Тема | Кол-во часов |
| 1 | Контрольная работа по теме: « Функции и графики. Предел функции и непрерывность. Обратные функции» | 1 |
| 2 | Контрольная работа на тему «Производная» | 1 |
| 3 | Контрольная работа на тему: « Применение производной» | 1 |
| 4 | Контрольная работа «Первообразная и интеграл» | 1 |
| 5 | Контрольная работа по теме: « Равносильность уравнений и неравенств. Уравнения-следствия» | 1 |
| 6 | Контрольная работа по теме: « Равносильность уравнений на множествах. Метод промежутков для уравнений и неравенств» | 1 |
| 7 | Контрольная работа по теме: « Системы уравнений с несколькими неизвестными» | 1 |
| 8 | Контрольная работа по теме: « Метод координат в пространстве» | 1 |
| 9 | Контрольная работа по теме: « Цилиндр, конус, шар» | 1 |
| 10 | Контрольная работа по теме: «Объемы тел» | 1 |
| 11 | Итоговая контрольная работа | 2 |
ИТОГО: 12 часов.
Содержание тем учебного курса
1. Функции и их графики (9 часов)
Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума. Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях.
Преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой 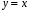 , растяжение и сжатие вдоль осей координат.
, растяжение и сжатие вдоль осей координат.
2. Предел функции и непрерывность (5 часов)
Понятие о непрерывности функции. Основные теоремы о непрерывных функциях.
Понятие о пределе функции в точке. Поведение функций на бесконечности. Асимптоты. Вертикальные и горизонтальные асимптоты графиков. Графики дробно-линейных функций.
3. Обратные функции (6 часов)
Сложная функция (композиция функций). Взаимно обратные функции. Область определения и область значений обратной функции. График обратной функции. Нахождение функции, обратной данной. Обратные тригонометрические функции, их свойства и графики.
4. Производная ( 11 часов).
Понятие о производной функции, физический и геометрический смысл производной. Уравнение касательной к графику функции. Производные суммы, разности, произведения и частного. Производные основных элементарных функций. Производные сложной и обратной функций. Вторая производная.
5. Применение производной (16 часов)
Применение производной к исследованию функций и построению графиков. Использование производных при решении уравнений и неравенств, при решении текстовых, физических и геометрических задач, нахождении наибольших и наименьших значений.
Примеры использования производной для нахождения наилучшего решения в прикладных задачах. Нахождение скорости для процесса, заданного формулой или графиком. Вторая производная и ее физический смысл.
6. Первообразная и интеграл (13 часов ).
Площадь криволинейной трапеции. Понятие об определенном интеграле. Первообразная. Первообразные элементарных функций. Правила вычисления первообразных. Формула Ньютона-Лейбница.
Примеры применения интеграла в физике и геометрии.
7.Равносильность уравнений и неравенств (4 часа)
Равносильные преобразования уравнений. Равносильные преобразования
8. Уравнения-следствия (8 часов)
Понятие уравнения-следствия. Возведение уравнения в четную степень. Потенцирование логарифмических уравнений. Другие преобразования, приводящие к уравнению-следствию.
9. Равносильность уравнений и неравенств системам (13 часов)
Решение уравнений с помощью систем. Решение неравенств с помощью систем
10. Равносильность уравнений на множествах (7 часов)
11. Равносильность неравенств на множествах (7 часов)
Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. . Решение иррациональных неравенств. Решение систем уравнений с двумя неизвестными простейших типов. Решение систем неравенств с одной переменной.
Доказательства неравенств. Неравенство о среднем арифметическом и среднем геометрическом двух чисел. Переход к пределам в неравенствах.
12. Метод промежутков для уравнений и неравенств (5 часов)
Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
13. Использование свойств функций при решении уравнений и неравенств (5 часов)
Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
14. Системы уравнений с несколькими неизвестными (8 часов)
Равносильность систем. Система –следствие. Метод замены неизвестных.
15. Повторение курса алгебры и математического анализа (16часов).
16. Векторы в пространстве (7 часов)
Понятие вектора. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число. Компланарные векторы. Разложение вектора по трем некомпланарным векторам.
17. Метод координат в пространстве (15 часов)
Декартовы координаты в пространстве. Формула расстояния между двумя точками. Уравнения сферы и плоскости. Формула расстояния от точки до плоскости.
Векторы. Модуль вектора. Равенство векторов. Сложение векторов и умножение вектора на число. Координаты вектора. Компланарные векторы. Разложение по трем некомпланарным векторам.
Угол между векторами. Скалярное произведение векторов.
Вычисления углов с вершиной внутри и вне круга угла между хордами и касательной. Теорема о произведении отрезков хорд. Теорема о касательной и секущей. Теорема о сумме квадратов сторон и диагоналей параллелограмма.
Вписанные и описанные многоугольники. Свойства и признаки вписанных и описанных четырехугольников.
Геометрические места точек.
Решение задач с помощью геометрических преобразований и геометрических мест.
Центральная симметрия. Осевая симметрия. Зеркальная симметрия. Параллельный перенос.
18.Тела и поверхности вращения (16 часов)
Цилиндр и конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения параллельные основанию.
Шар и сфера, их сечения. Эллипс, гипербола, парабола как сечения конуса. Касательная плоскость к сфере. Сфера, вписанная в многогранник. Сфера, описанная около многогранника.
Цилиндрические и конические поверхности
18 .Объемы тел (16 часов)
Понятие об объеме тела. Отношение объемов подобных тел.
Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формулы объема шара и площади сферы.
19. Повторение (17часов)
Вычисление площадей многогранников. Вычисление объёмов многогранников. Вычисление площадей и объёмов тел вращения. Методы решения задач планиметрии. Векторы.
Требования к уровню подготовки обучающихсяВ результате изучения математики на профильном уровне в старшей школе обучающийся должен:
Знать/понимать
значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки;
идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;
универсальный характер законов логики математических рассуждений, их применимость в различных областях человеческой деятельности;
различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
вероятностных характер различных процессов и закономерностей окружающего мира.
Числовые и буквенные выражения.Уметь:
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
применять понятия, связанные с делимостью целых чисел, при решении математических задач;
находить корни многочленов с одной переменной, раскладывать многочлены на множители;
проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, при необходимости используя справочные материалы и простейшие вычислительные устройства.
Функции и графики.Уметь:
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций, выполнять преобразования графиков;
описывать по графику и по формуле поведение и свойства функций;
решать уравнения, системы уравнений, неравенства, используя свойства функций и их графические представления;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для описания и исследования с помощью функций реальных зависимостей, представления их графически; интерпретации графиков реальных процессов.
Начала математического анализа.Уметь:
находить сумму бесконечно убывающей геометрический прогрессии;
Уравнения и неравенства.Уметь:
решать рациональные, показательные и логарифмические уравнения и неравенства, иррациональные и тригонометрические уравнения, их системы;
доказывать несложные неравенства;
решать текстовые задачи с помощью составления уравнений, и неравенств, интерпретируя результат с учетом ограничений условия задачи;
изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем;
находить приближенные решения уравнений и их систем, используя графический метод;
решать уравнения, неравенства и системы с применением графических представлений, свойств функций, производной;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для
построения и исследования простейших математических моделей.
Элементы комбинаторики, статистики и теории вероятностей.
Уметь:
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля;
вычислять, в простейших случаях, вероятности событий на основе подсчета числа исходов.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для анализа реальных числовых данных, представленных в виде диаграмм, графиков; для анализа информации статистического характера.
Геометрия.
Знать и уметь:
распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;
описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;
анализировать в простейших случаях взаимное расположение объектов в пространстве;
изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;
строить простейшие сечения куба, призмы, пирамиды;
решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);
использовать при решении стереометрических задач планиметрические факты и методы;
проводить доказательные рассуждения в ходе решения задач;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Учебно-методическое обеспечение
Алгебра и начала анализа: учебник для 11 класса общеобразовательных учреждений. Составители:. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. — М.: Просвещение, 20013.
«Алгебра и начала анализа. Дидактические материалы для 11 класса базовый и профильный уровни 3 –е издание, - М. Просвещение, 2015. Авторы: М. К. Потапов и А. В. Шевкин»
«Алгебра и начала математического анализа. Тематические тесты для 11 класса базовый и профильный уровни, - М. Просвещение, 2015. Автор Ю. В. Шепелева»
«Алгебра и начала математического анализа 11 класс. Книга для учителя. Базовый и профильный уровни, - М. Просвещение, 2015. Авторы: М. К. Потапов и А. В. Шевкин».
Геометрия, 10-11: Учебник для общеоб. учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Позняк, Л. С. Киселева - М.: Просвещение, 2014
Б.Г. Зив. Дидактические материалы по геометрии для 11 класса. – М. Просвещение, 20013 г
Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по алгебре для 11 класса.- 4-е издание, испр. и доп.- М.:Илекса, 2012,- 175 с.
Саакян С.М. Изучение геометрии в 10-11 классах: книга для учителя/ С.М. Саакян, В.Ф. Бутузов.- М. Просвещение, 2010.
Б.Г. Зив. Дидактические материалы по геометрии для 11 класса. – М. Просвещение, 2010.
Б.Г. Зив, В.М. Мейлер, А.П. Баханский. Задачи по геометрии для 7 – 11 классов. – М.: Просвещение, 2003.
Материально-техническое и информационно-техническое обеспечение
Интерактивная доска
Проектор
3. Компьютер
4. Виртуальная школа Кирилла и Мефодия
| http://www.school.edu.ru | Российский общеобразовательный портал, где содержатся образовательные ресурсы для учеников, учителей, родителей, администраторов. Учебные, научно - популярные, познавательные и другие материалы по основным школьным дисциплинам. Вопросы здоровья и психологии школьников. Газета «Первое сентября» и приложения к ней |
| http://school-collection.edu.ru/ | Единая коллекция цифровых образовательных ресурсов |
| http://www.prazdnik.by | Портал для детей и взрослых. |
| http://www.it-n.ru/ | Сайт творческих учителей. |
| http://mail.redu.ru | Исследовательская работа школьников |
| http://festival.1september.ru | Фестиваль педагогических идей «Открытый урок» |
Конец формы
Календарно-тематическое планирование
| № ур | Наименование изучаемой темы по алгебре | дата | Наименование изучаемой темы по геометрии | дата | ||||
| п | ф | п | Ф | |||||
| | Элементарные функции |
|
|
|
|
| ||
| |
|
|
| Понятие вектора в пространстве |
|
| ||
| | Область определения и область изменения функции. Ограниченность функции |
|
|
|
|
| ||
| | Четность, нечетность, периодичность функций |
|
|
|
|
| ||
| |
|
|
| Сложение и вычитание векторов |
|
| ||
| | Четность, нечетность, периодичность функций |
|
|
|
|
| ||
| | Промежутки возрастания, убывания, знакопостоянства и нули функции |
|
|
|
|
| ||
| |
|
|
| Умножение вектора на число. |
|
| ||
| | Промежутки возрастания, убывания, знакопостоянства и нули функции |
|
|
|
|
| ||
| | Исследование функций и построение их графиков элементарными методами |
|
|
|
|
| ||
| |
|
|
| Компланарные векторы. Правило параллелепипеда. |
|
| ||
| | Основные способы преобразования графиков |
|
|
|
|
| ||
| | Графики функций, связанных с модулем |
|
|
|
|
| ||
| |
|
|
| Разложение вектора по трем некомпланарным векторам |
|
| ||
| | Понятие предела функции |
|
|
|
|
| ||
| | Односторонние пределы |
|
|
|
|
| ||
| |
|
|
| Решение задач по теме «Векторы в пространстве и метод координат» |
|
| ||
| | Свойства пределов функций |
|
|
|
|
| ||
| | Понятие непрерывности функции |
|
|
|
|
| ||
| |
|
|
| Решение задач по теме «Векторы в пространстве и метод координат» |
|
| ||
| | Непрерывность элементарных функций |
|
|
|
|
| ||
| | Понятие обратной функции |
|
|
|
|
| ||
| |
|
|
| Прямоугольная система координат в пространстве |
|
| ||
| | Взаимно обратные функции |
|
|
|
|
| ||
| | Обратные тригонометрические функции |
|
|
|
|
| ||
| |
|
|
| Координаты вектора |
|
| ||
| | Обратные тригонометрические функции |
|
|
|
|
| ||
| | Примеры использования обратных тригонометрических функций |
|
|
|
|
| ||
| |
|
|
| Связь между координатами точки и координатами вектора |
|
| ||
| | Контрольная работы №1 по теме «Функция, графики предел функции и обратные функции» |
|
|
|
|
| ||
| | Анализ контрольной работы. Понятие производной |
|
|
|
|
| ||
| |
|
|
| Простейшие задачи в координатах. |
|
| ||
| | Производная суммы. |
|
|
|
|
| ||
| | Производная разности. |
|
|
|
|
| ||
| |
|
|
| Простейшие задачи в координатах. |
|
| ||
| | Непрерывность функции, имеющих производную. Дифференциал. |
|
|
|
|
| ||
| | Производная произведения. |
|
|
|
|
| ||
| |
|
|
| Решение задач по теме: «Простейшие задачи в координатах» |
|
| ||
| | Производная частного |
|
|
|
|
| ||
| |
|
|
| Угол между векторами |
|
| ||
| | Производные элементарных функций |
|
|
|
|
| ||
| | Производная сложной функции |
|
|
|
|
| ||
| |
|
|
| Скалярное произведение векторов |
|
| ||
| | Производная сложной функции |
|
|
|
|
| ||
| | Контрольная работа №2 по теме «Производная» |
|
|
|
|
| ||
| |
|
|
| Вычисление углов между прямыми и плоскостями |
|
| ||
| | Анализ контрольной работы. Максимум и минимум функции |
|
|
|
|
| ||
| | Максимум и минимум функции |
|
|
|
|
| ||
| |
|
|
| Вычисление углов между прямыми и плоскостями |
|
| ||
| | Уравнение касательной |
|
|
|
|
| ||
| | Уравнение касательной |
|
|
|
|
| ||
| |
|
|
| Уравнение плоскости. Расстояние от точки до плоскости. |
|
| ||
| | Приближенные вычисления |
|
|
|
|
| ||
| | Возрастание и убывание функций |
|
|
|
|
| ||
| |
|
|
| Центральная симметрия. Осевая симметрия |
|
| ||
| | Возрастание и убывание функций |
|
|
|
|
| ||
| | Производные высших порядков |
|
|
|
|
| ||
| |
|
|
| Симметрия. Параллельный перенос. |
|
| ||
| | Экстремум функции с единственной критической точкой |
|
|
|
|
| ||
| | Экстремум функции с единственной критической точкой |
|
|
|
|
| ||
| |
|
|
| Контрольная работа по теме: «Метод координат в пространстве» |
|
| ||
| | Задачи на максимум и минимум |
|
|
|
|
| ||
| | Задачи на максимум и минимум |
|
|
|
|
| ||
| |
|
|
| Анализк онтрольной работы |
|
| ||
| | Асимптоты. Дробно-линейная функция |
|
|
|
|
| ||
| | Построение графиков функций с применением производная |
|
|
|
|
| ||
| |
|
|
| Понятие цилиндра |
|
| ||
| | Построение графиков функций с применением производная |
|
|
|
|
| ||
| | Контрольная работа №3 по теме «Применение производной» |
|
|
|
|
| ||
| |
|
|
| Площадь поверхности цилиндра. |
|
| ||
| | Анализ контрольной работы. Понятие первообразной |
|
|
|
|
| ||
| | Понятие первообразной |
|
|
|
|
| ||
| |
|
|
| Цилиндр. |
|
| ||
| | Понятие первообразной |
|
|
|
|
| ||
| | Площадь криволинейной трапеции |
|
|
|
|
| ||
| |
|
|
| Понятие конуса. |
|
| ||
| | Определенный интеграл |
|
|
|
|
| ||
| | Определенный интеграл |
|
|
|
|
| ||
| |
|
|
| Площадь поверхности конуса. |
|
| ||
| | Приближенное вычисление определенного интеграла |
|
|
|
|
| ||
| | Формула Ньютона-Лейбница |
|
|
|
|
| ||
| |
|
|
| Усеченный конус. |
|
| ||
| | Формула Ньютона-Лейбница |
|
|
|
|
| ||
| | Формула Ньютона-Лейбница |
|
|
|
|
| ||
| |
|
|
| Сфера и шар |
|
| ||
| | Свойства определенных интегралов |
|
|
|
|
| ||
| | Применение определенных интегралов в геометрических и физических задачах |
|
|
|
|
| ||
| |
|
|
| Уравнение сферы |
|
| ||
| | Контрольная работа №4 по теме «Первообразная и интеграл» |
|
|
|
|
| ||
| | Анализ контрольной работы. Равносильные преобразования уравнений |
|
|
|
|
| ||
| |
|
|
| Взаимное расположение сферы и плоскости. |
|
| ||
| | Равносильные преобразования уравнений |
|
|
|
|
| ||
| | Равносильные преобразования неравенств |
|
|
|
|
| ||
| |
|
|
| Площадь сферы. |
|
| ||
| | Равносильные преобразования неравенств |
|
|
|
|
| ||
| | Понятие уравнения-следствия |
|
|
|
|
| ||
| |
|
|
| Разные задачи на многогранники, цилиндр, конус, шар. |
|
| ||
| | Возведение уравнения в четную степень |
|
|
|
|
| ||
| | Возведение уравнения в четную степень |
|
|
|
|
| ||
| |
|
|
| Разные задачи на многогранники, цилиндр, конус, шар. |
|
| ||
| | Потенцирование логарифмических уравнений |
|
|
|
|
| ||
| | Потенцирование логарифмических уравнений |
|
|
|
|
| ||
| |
|
|
| Сечения цилиндрической и конической поверхностей. |
|
| ||
| | Другие преобразования, приводящие к уравнению-следствию |
|
|
|
|
| ||
| | Применение нескольких преобразований, приводящих к уравнению-следствию |
|
|
|
|
| ||
| |
|
|
| Сечения цилиндрической и конической поверхностей. |
|
| ||
| | Применение нескольких преобразований, приводящих к уравнению-следствию |
|
|
|
|
| ||
| | Основные понятия |
|
|
|
|
| ||
| |
|
|
| Контрольная работа по теме «Тела вращения» |
|
| ||
| | Решение уравнений с помощью систем |
|
|
|
|
| ||
| | Решение уравнений с помощью систем |
|
|
|
|
| ||
| |
|
|
| Анализ контрольной работы |
|
| ||
| | Решение уравнений с помощью систем (продолжение) |
|
|
|
|
| ||
| | Решение уравнений с помощью систем (продолжение) |
|
|
|
|
| ||
| |
|
|
| Понятие объема. |
|
| ||
| | Уравнения вида |
|
|
|
|
| ||
| | Уравнения вида |
|
|
|
|
| ||
| |
|
|
| Объём прямоугольного параллелепипеда |
|
| ||
| | Решение неравенств с помощью систем |
|
|
|
|
| ||
| | Решение неравенств с помощью систем |
|
|
|
|
| ||
| |
|
|
| Объём прямоугольного параллелепипеда |
|
| ||
| | Решение неравенств с помощью систем (продолжение) |
|
|
|
|
| ||
| | Решение неравенств с помощью систем (продолжение) |
|
|
|
|
| ||
| |
|
|
| Объём прямой призмы и цилиндра |
|
| ||
| | Неравенства вида |
|
|
|
|
| ||
| | Неравенства вида |
|
|
|
|
| ||
| |
|
|
| Объём прямой призмы и цилиндра |
|
| ||
| | Основные понятия |
|
|
|
|
| ||
| | Возведение уравнения в четную степень |
|
|
|
|
| ||
| |
|
|
| Объём наклонной призмы. |
|
| ||
| | Возведение уравнения в четную степень |
|
|
|
|
| ||
| | Умножение уравнения на функцию |
|
|
|
|
| ||
| |
|
|
| Объём наклонной призмы. |
|
| ||
| | Другие преобразования уравнений |
|
|
|
|
| ||
| | Применение нескольких преобразований |
|
|
|
|
| ||
| |
|
|
| Объём пирамиды |
|
| ||
| | Контрольная работа №5 по теме «Уравнения» |
|
|
|
|
| ||
| | Анализ контрольной работы. Основные понятия |
|
|
|
|
| ||
| |
|
|
| Объём пирамиды |
|
| ||
| | Возведение неравенств в четную степень |
|
|
|
|
| ||
| | Возведение неравенств в четную степень |
|
|
|
|
| ||
| |
|
|
| Объём конуса |
|
| ||
| | Умножение неравенства на функцию |
|
|
|
|
| ||
| | Другие преобразования неравенств |
|
|
|
|
| ||
| |
|
|
| Объём конуса |
|
| ||
| | Применение нескольких преобразований |
|
|
|
|
| ||
| | Нестрогие неравенства |
|
|
|
|
| ||
| |
|
|
| Объём шара |
|
| ||
| | Уравнения с модулями |
|
|
|
|
| ||
| | Неравенства с модулями |
|
|
|
|
| ||
| |
|
|
| Объём шара |
|
| ||
| | Метод интервалов для непрерывных функций |
|
|
|
|
| ||
| | Метод интервалов для непрерывных функций |
|
|
|
|
| ||
| |
|
|
| Объём шара и площадь сферы |
|
| ||
| | Контрольная работа №6 по теме «Неравенства» |
|
|
|
|
| ||
| | Анализ контрольной работы. Использование областей существования функции |
|
|
|
|
| ||
| |
|
|
| Контрольная работа №3 по теме «Объемы тел» |
|
| ||
| | Использование неотрицательности функции |
|
|
|
|
| ||
| | Использование ограниченности функции |
|
|
|
|
| ||
| |
|
|
| Анализ контрольной работы. Повторение по теме «Объемы тел» |
|
| ||
| | Использование монотонности и экстремумов функции |
|
|
|
|
| ||
| | Использование свойств синуса и косинуса |
|
|
|
|
| ||
| |
|
|
| Повторение «Аксиомы стереометрии» |
|
| ||
| | Равносильность систем |
|
|
|
|
| ||
| | Равносильность систем |
|
|
|
|
| ||
| |
|
|
| Повторение по теме «Аксиомы стереометрии» |
|
| ||
| | Система-следствие |
|
|
|
|
| ||
| | Система-следствие |
|
|
|
|
| ||
| |
|
|
| Повторение по теме «Параллельность прямых, параллельность прямой и плоскости. Скрещивающиеся прямые. Параллельность плоскостей» |
|
| ||
| | Метод замены неизвестных |
|
|
|
|
| ||
| | Метод замены неизвестных |
|
|
|
|
| ||
| |
|
|
| Повторение по теме «Перпендикулярность прямой и плоскости. Теорема о трех перпендикулярах. Угол между прямой и плоскостью» |
|
| ||
| | Рассуждения с числовыми значениями при решении уравнений и неравенств |
|
|
|
|
| ||
| | Контрольная работа №7 по теме «Неравенства» |
|
|
|
|
| ||
| | Анализ контрольной работы. |
|
|
|
|
| ||
| |
|
|
| Повторение по теме «Двугранный угол. Перпендикулярность плоскостей» |
|
| ||
| | Повторение по теме «Числа» |
|
|
|
|
| ||
| | Повторение по теме «Алгебраические выражения» |
|
|
|
|
| ||
| |
|
|
| Повторение по теме «Многогранники» |
|
| ||
| | Повторение по теме «Алгебраические выражения» |
|
|
|
|
| ||
| | Повторение по теме «Функция» |
|
|
|
|
| ||
| |
|
|
| Повторение по теме «Многогранники» |
|
| ||
| | Повторение по теме «Функция» |
|
|
|
|
| ||
| | Повторение по теме «Функция» |
|
|
|
|
| ||
| |
|
|
| Повторение по теме «Векторы в пространстве. Действия над векторами. Скалярное произведение векторов» |
|
| ||
| | Повторение по теме «Решение уравнений и неравенств» |
|
|
|
|
| ||
| | Повторение по теме «Решение уравнений и неравенств» |
|
|
|
|
| ||
| |
|
|
| Повторение по теме «Цилиндр, конус и шар, площади их поверхностей» |
|
| ||
| | Повторение по теме «Решение уравнений и неравенств» |
|
|
|
|
| ||
| | Повторение по теме «Решение уравнений и неравенств» |
|
|
|
|
| ||
| |
|
|
| Повторение по теме «Объемы тел» |
|
| ||
| | Повторение по теме «Производная. Применение производной» |
|
|
|
|
| ||
| | Повторение по теме «Производная. Применение производной» |
|
|
|
|
| ||
| |
|
|
| Повторение по теме «Объемы тел» |
|
| ||
| | Повторение по теме «Производная. Применение производной» |
|
|
|
|
| ||
| | Повторение по теме «Производная. Применение производной» |
|
|
|
|
| ||
| |
|
|
| Повторение по теме «Многогранники» |
|
| ||
| |
|
|
| Повторение по теме «Тела вращения» |
|
| ||
| | Итоговая контрольная работа |
|
|
|
|
| ||
| | Итоговая контрольная работа |
|
|
|
|
| ||
| | Анализ контрольной работы |
|
|
|
|
| ||
| | Повторение «Текстовые задачи» |
|
|
|
|
| ||
| |
|
|
| Решение задач по теме «Комбинации с описанными сферами» |
|
| ||
| | Решение задач по теме «Текстовые задачи». Подведение итогов второго полугодия. |
|
|
|
|
| ||

 Получите свидетельство
Получите свидетельство Вход
Вход












 Рабочая программа по математике 11 класс (профильное обучение) по учебникам С.М. Никольского, Л.М. Атанасяна (69.71 KB)
Рабочая программа по математике 11 класс (профильное обучение) по учебникам С.М. Никольского, Л.М. Атанасяна (69.71 KB)
 0
0 856
856 125
125 Нравится
0
Нравится
0


