Проверочная работа по теме : «Множества»
Часть А
| № п/п | Задание | 1 вариант | 2 вариант |
| | Выберите верное утверждение: | Что такое множество? а) достоверное знание, соответствие которого объективным явлениям и предметам окружающего мира подтверждено практикой; б) наука о законах и формах правильного мышления; в)объединение некоторых объектов или предметов в единую совокупность по каким-либо общим свойствам или законам. | При пересечении двух множеств получаем третье множество, которое … а)всегда состоит из одного элемента; б)может состоять из одного элемента; в)всегда не содержит элементов; г)иногда не содержит элементы.
|
| | Выберите верное утверждение: | Если все элементы множества А входят в множество В, то можно сказать, что : а) А – образ множества В; б) А – подмножество В; в) В – прообраз множества А; г) В – подмножество А. | Множества бывают: а) бесконечные; б)конечные; в) пустое; г)единичное. |
| | Выберите верное утверждение: | Существует множество без элементов? а)да; б)нет; в)в любом множестве не менее 1 элемента; г) в любом множестве не более 1 элемента. | При обозначении множеств используют: а)только круглые скобки; б)только фигурные скобки; в)иногда круглые, иногда фигурные, но только один вид скобок; г)иногда круглые, иногда фигурные, иногда одновременно оба вида скобок. |
| | Укажите равные множества: | а) {2;4;2;5},{2;4;5}, б) {10},{-10}, в) {10;35},{10;-35}, г) {60;80},{80;60}. | а) {50;9},{9;50}, б) {11},{-11}, в) {0;35},{0;-35}, г){8;4;8;5},{8;5;4}. |
| | Определить ,какое из множеств является подмножеством множества А: | А={10;20;30;40;50;60} а) {10;20;30;40;50;60;70}, б) {10}, в) {10;35}, г) {60;80}. | А={5;15;25;35;45;55;65} а) {55}, б) {5;25;50}, в) {25;55;75}, г) {5;70}. |
| | Какое из множеств определяет А ∪ В: | А={1;2;3;4;5} В={3;4;5;6;7} а) {3;4;5}, б) {1;2;3;4;5}, в) {1;2;3;4;5;6;7}, г) {1;7}. | А={2;4;6;8;10}В={8;10;12;14} а) {8;10;12;14}, б) {8;10}, в) {2;4;6;8}, г) {2;4;6;8;10;12;14}. |
| | Какое из множеств определяет А ∩ В: | А={1; 3; 5;7;9} В={1;2;3;4} а) {1;3;5;7}, б) {1;2;3;4;5;7;9}, в) {1;3}, г) {1}. | А={2;4; 6;8;10} В={2;4;8;9} а) {2;4; 6;8;10}, б) {2;4;8;9}, в) {2;4;8}, г) {2}. |
| | О какой операции над множествами идёт речь в задаче: а) Объединение множеств б) Пересечение множеств в) Разность множеств г) Дополнение множества | На тарелке лежало 13 персиков. Вова взял 7 персиков. Сколько персиков осталось на тарелке?
| Дети первого класса «А» изготовили на праздник 15 фонариков, дети первого «Б» 20 фонариков. А ученики первого «В» изготовили столько фонариков, сколько ученики 1 «А» и 1»Б» вместе. Сколько фонариков изготовили ученики 1 «В» класса? |
| | Какое из множеств определяет А \ в | А={2;4; 6;8;10},В={2;4;8;9} а) {2;4; 6;8;10}, б) {2;4;8;9}, в) {2;4;8}, г) {6;10}. | А={1; 3; 5;7;9}, В={1;2;3;4} а) {1;3;5;7}, б) {1;2;3;4;5;7;9}, в) {5;7;9}, г) {1;3}. |
| | Укажите пустые множества среди следующих: | а) множество целых корней уравнения б) множество целых корней уравнения в) множество натуральных чисел ,меньших 1; г) множество действительных корней уравнения | а) множество целых корней уравнения б) множество целых корней уравнения в) множество действительных корней уравнения г)множество натуральных чисел ,меньших 2; |
| | Укажите все элементы множества: | { x | { x |
| | Задайте множество в виде некоторого интервала числовой прямой: | { x | { x |
Часть В
|
| 1 вариант |
|
| 13 | В круг вписан квадрат. Пусть А-множество точек данного круга и В-множество точек квадрата. Найдите А | В квадрат вписан круг. Пусть А-множество точек данного квадрат и В-множество точек круга. Найдите А |
| 14 | Из 40 учеников 5 класса 32 человека посещают спортивные секции , 21 -музыкальную школу, а 15 спортивную секцию и музыкальную школу. Сколько учащихся не занимаются ни в спортивной секции, ни в музыкальной школе? | В классе - 30 учеников. Из них 18 тренируются в секции легкой атлетики, 10 - в секции плавания, 3 - в обеих секциях. Сколько учеников класса не посещают ни одной из этих секций? |
| 15 | Укажите все элементы множества { x | Укажите все элементы множества { x |
| 16 | Пусть А={x ; В={-5;3;5;7}.Найдите А | Пусть А={x ; В={1;3;5;7}.Найдите А |
| 17 | Найдите объединение и пересечение множества решений неравенств, в которых переменная x - действительное число -2 | Найдите объединение и пересечение множества решений неравенств, в которых переменная x – действительное число -7 ≤ х |
| 18 | Пусть А={-4;-3; -2;-1;0;1; 2}, В={4;3;2;1;0;-1;-2}, С={-4;-3;…..;3;4}. Найдите множества А | Пусть А={-5;-4;-3; -2;-1;0;1}, В={3;2;1;0;-1;-2;-3}, С={-3;-2;…..;2;3}. Найдите множества А |
| 19 | Пусть А={x В={x Найдите А ∩ В. | Пусть А={x В={x Найдите А ∩ В. |

 Получите свидетельство
Получите свидетельство Вход
Вход



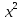 - 9=0;
- 9=0;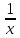 = 0
= 0 = 0
= 0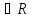 ;
; 0}
0}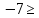 0}
0} B , А ∩ В.
B , А ∩ В.








 Проверочная работа по теме "Множества и операции над ними" (25.74 KB)
Проверочная работа по теме "Множества и операции над ними" (25.74 KB)
 0
0 20446
20446 1324
1324 Нравится
0
Нравится
0


