Практическая работа по теме: «Алгебра (логика)высказываний»
|
| 1 вариант | 2 вариант | |||||||||||||||||||||||||||||||
| 1 | Логика-это а) наука о формах, в которых протекает человеческое мышление и о законах ,которым оно подчиняется; б) раздел математики, посвященный изучению математических доказательств и вопросов оснований математики; в) всякое утверждение, о котором можно определенно, объективно и однозначно можно сказать истинно оно или ложно; г) функция, принимающая одно из двух значений 0 и 1. | Раздел математики, посвященный изучению математических доказательств и вопросов оснований математики: а) логика; б) математическая логика; в) высказывание; г) функция истинности.
| |||||||||||||||||||||||||||||||
| 2 | Всякое утверждение, о котором можно определенно, объективно и однозначно сказать истинно оно или ложно: а) высказывание; б) логика; в) функция истинности; г) математическая логика. | Функция истинности: а) Функция, принимающая значение «истина»; б) Функция, принимающая значения «истина», «ложь», «ни истина, ни ложь»; в) Функция, которая на множестве всех высказываний, каждому высказыванию ставит в соответствие единственное значение 0 или 1; г) Функция, которая на множестве всех высказываний, каждому высказыванию ставит в соответствие значения 0 и 1; | |||||||||||||||||||||||||||||||
| 3 | Определите, какие из следующих предложений являются высказываниями, а какие нет. Определите их истинность или ложность. | ||||||||||||||||||||||||||||||||
| а) Математика – царица наук; б) Ты знаешь теорию вероятностей? в) Выучи урок, заданный по алгебре. г) Есть школьники, которые знают математику на “5”. д) Все школьники любят информатику. | а) Для каждого из нас учить второй иностранный язык легче, чем первый. б) Какой иностранный язык ты изучаешь? в) Переводчик должен знать хотя бы два языка. г) Учи русский язык. д) Некоторые школьники предпочитают изучать китайский язык. | ||||||||||||||||||||||||||||||||
| 4 | Укажите какие высказывания простые ,а какие сложные ,определите их значения (Истина или Ложь). | ||||||||||||||||||||||||||||||||
| а) Если две прямые параллельны, то они пересекаются. б) Идет урок информатики. в) На следующем уроке будет контрольная работа или объяснение новой темы. г) Сегодня или завтра в гости приедет брат. | а) Треугольники с равными сторонами – равнобедренные. б) Число 3 больше числа 2. в) Тогда и только тогда, когда я вижу вас, у меня нет слов, чтобы высказать вам все. г) Завтра в нашем театре премьера. | ||||||||||||||||||||||||||||||||
| 5 | Укажите, в каких сложных высказываниях присутствует | ||||||||||||||||||||||||||||||||
| логический союз конъюнкция: а) Если будет хорошая погода, то мы пойдем в парк. б) Я поеду в горы тогда и только тогда, когда куплю горные лыжи. в) Он заболел или забыл о нашем договоре. г)Неверно, что Саша приходил ко мне вчера домой и приносил книгу. | логический союз дизъюнкция: а) Я вчера не ходил в бассейн. б) Завтра я не пойду в школу и пойду в поликлинику. в) Зимой мы обычно катаемся на коньках и лыжах и не купаемся в пруду. г) На следующем уроке будет контрольная или опрос. | ||||||||||||||||||||||||||||||||
| 6 | Логическое умножение-это а) конъюнкция; б) дизъюнкция; в) импликация; г) эквиваленция. | Логическое сложение-это а) импликация; б) эквиваленция; в) дизъюнкция; г) конъюнкция. | |||||||||||||||||||||||||||||||
| 7 | Логическое следствие-это а) конъюнкция; б) дизъюнкция; в) импликация; г) эквиваленция. | Равносильность-это а) импликация; б) конъюнкция; в) дизъюнкция; г) эквиваленция. | |||||||||||||||||||||||||||||||
| 8 | Какой логической операции соответствует таблица истинности?
а)дизъюнкция; б)конъюнкция; в)эквиваленция; г)импликация. | Какой логической операции соответствует таблица истинности?
а)дизъюнкция; б)конъюнкция; в)эквиваленция; г)импликация. | |||||||||||||||||||||||||||||||
| 9 | Выбрать верный порядок выполнения операций: а) отрицание, импликация, конъюнкция, дизъюнкция, эквиваленция; б) отрицание, конъюнкция, эквиваленция, дизъюнкция, импликация; в) отрицание, эквиваленция, конъюнкция, дизъюнкция, импликация; г) отрицание, конъюнкция, дизъюнкция, импликация ,эквиваленция. | Выбрать верный порядок выполнения операций: а) отрицание, импликация, конъюнкция, дизъюнкция, эквиваленция; б) отрицание, конъюнкция, дизъюнкция, импликация ,эквиваленция; в) отрицание, эквиваленция, конъюнкция, дизъюнкция, импликация; г)отрицание, конъюнкция, эквиваленция, дизъюнкция, импликация. | |||||||||||||||||||||||||||||||
| 10 | Высказывание называется элементарным или простым, если: а) любая часть этого высказывания – высказывание; б) любая часть этого высказывания не является высказыванием; в) оно состоит из одного предложения; г) оно состоит из одного слова. | Высказывание называется составным, если: а) любая часть этого высказывания – высказывание; б) любая часть этого высказывания не является высказыванием; в) оно состоит из одного предложения; г) оно состоит из одного слова. | |||||||||||||||||||||||||||||||
| 11 | Какое логическое выражение соответствует высказыванию: «Точка X принадлежит интервалу (А; В)». а) (ХВ) б) (ХА) и (Х в) ¬ (Х г) (ХА) или (ХВ). | Какое логическое выражение соответствует высказыванию: «Точка X не принадлежит интервалу (А; В)». а) (ХВ) б) (ХА) и (Х в) ¬ (Х г) (ХА) или (ХВ). | |||||||||||||||||||||||||||||||
| 12 | Высказывания A и B соединены операцией дизъюнкции. Новое высказывание, полученное таким образом, ложно тогда, когда: а) высказывание A ложно, а высказывание B истинно; б) высказывание A истинно, а высказывание B ложно; в) высказывание A ложно и высказывание B ложно; г) высказывание A истинно и высказывание B истинно.Начало формы | Высказывания A и B соединены операцией конъюнкции. Новое высказывание, полученное таким образом, истинно тогда, когда: а) высказывание A ложно, а высказывание B истинно; б) высказывание A истинно, а высказывание B ложно; в) высказывание A ложно и высказывание B ложно; г) высказывание A истинно и высказывание B истинно.Начало формы | |||||||||||||||||||||||||||||||
| 13 | С помощью логической операции эквивалентность из высказываний A и B получается высказывание, которое: а) истинно, когда истинно высказывание B; б) истинно, когда оба высказывания A и B истинны; в) не может быть ни истинным, ни ложным; г)истинно, когда оба высказывания A и B истинны, или оба ложны.Начало формыКонец формы | С помощью логической операции импликация из высказываний A и B получается высказывание, которое: а) ложно, когда оба высказывания A и В ложно; б) ложно, когда высказывание A и В истинно; в) не может быть ни истинным, ни ложным; г)ложно, когда высказывание A истинно и В ложно. | |||||||||||||||||||||||||||||||
| 14 | Логической единице (1) равно следующее выражение: а) 0∧1; б)1∨0; в)0∧1∨1; г)1∧1∧0. | Логическому нулю (0) равно следующее выражение: а) 0∧1; б)1∨0; в)0∧1∧0; г)1∧1∧0. | |||||||||||||||||||||||||||||||
| 15 | Установите правильную последовательность операций в выражении: | ||||||||||||||||||||||||||||||||
| ( (А ∧ а) ∧→ ∨ ¬ б) → ¬ ∧∨ в) ¬ ∧∨ → г) ¬ ∨ → ∧ | ( ( а) ∧→ ∨ ¬ б) → ¬ ∧∨ в) ¬ ∧∨ → г) ¬ ∨ → ∧ | ||||||||||||||||||||||||||||||||
| 16 | Для построения логической схемы, реализующей функцию Начало формы а)а)одна двухвходовая схема "ИЛИ", две двухвходовые схемы "И"; | Для построения логической схемы, реализующей функцию (( , потребуются:Начало формы а)а)четыре схемы "НЕ", три трёхвходовых схемы "И", одна двухвходовая схема "ИЛИ"; | |||||||||||||||||||||||||||||||
| 17 | Составьте несколько сложных высказываний, используя следующие простые высказывания: | ||||||||||||||||||||||||||||||||
| а) Я видел Мишу на улице. б)Он скоро окончит институт. в)Он будет учиться в аспирантуре. | а) Завтра будет холодно. б)Завтра пойдет снег. в)Завтра будет тепло. | ||||||||||||||||||||||||||||||||
| 18 | Самостоятельно придумайте по одному высказыванию с каждой, известной вам логической связкой. | ||||||||||||||||||||||||||||||||
| 19 | Придумайте 2 высказывания, которые не являются объектами алгебры логики. | Придумайте 2 высказывания, которые не являются объектами алгебры логики. | |||||||||||||||||||||||||||||||
| 20 | Найдите значения логических выражений: а)F1 = (0∨0) ∨ (1∨0). б)F2 =(0 ∧ 0) ∧ (0 ∧ 1). в)F3 = 0 ∧ (1∧ 0 ) ∨(1∨1). г)F4 = д)F5 =( | Найдите значения логических выражений: а)F1 = (0∨1) ∨ (1∨0). б)F2 =(0 ∧ 0) ∧ (0 ∧ 1). в)F3 = 0 ∨ (1∧ 0 ) ∨(1∨1). г)F4 = д)F5 =( | |||||||||||||||||||||||||||||||
| 21 | Для логических выражений сформулируйте составные высказывания на обычном языке: | ||||||||||||||||||||||||||||||||
| а) (y1 и yyy4) б) (x= y) и (x=Z) в) не (xx г) (3x)и(xy | а) (y4 и yyy7) б) (x= y) и (x=Z) в) не (xx г) (0x)и(xy | ||||||||||||||||||||||||||||||||
| 22 | Даны высказывания: А = {3+3=7}, B= {3+3=6}.Определить истинность высказываний: А∧В, | Даны высказывания: А = {5*5=25}, B= {5+5=11}.Определить истинность высказываний: А∧В, | |||||||||||||||||||||||||||||||
| 23 | Выяснить, является ли следующая формула тождественно истинной: | ||||||||||||||||||||||||||||||||
| ((А∨В) ∧ | А ∧ В ∨ | ||||||||||||||||||||||||||||||||
| 24 | Выяснить, является ли следующая формула тождественно ложной: | ||||||||||||||||||||||||||||||||
| | | ||||||||||||||||||||||||||||||||
| 25 | Выяснить, является ли следующая формула выполнимой: | ||||||||||||||||||||||||||||||||
| | | ||||||||||||||||||||||||||||||||
| 26 | Составить таблицу истинности для логического выражения: | ||||||||||||||||||||||||||||||||
| F= ( | F= | ||||||||||||||||||||||||||||||||
| 27 | Составить таблицу истинности для логического выражения: | ||||||||||||||||||||||||||||||||
| F= | F= | ||||||||||||||||||||||||||||||||

 Получите свидетельство
Получите свидетельство Вход
Вход



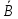 )∨ С )→В:
)∨ С )→В: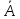 ∧
∧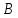 )∨ С )→В:
)∨ С )→В: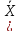 ∨ Y ∨ Z ) ∧ (X ∧ Y ∧
∨ Y ∨ Z ) ∧ (X ∧ Y ∧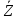 ), потребуются:
), потребуются: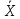 ∧
∧ 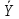 ∧
∧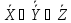 )
)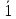 ∧ (1∨0) ∨(
∧ (1∨0) ∨( ∧ 0).
∧ 0).








 Проверочная работа по теме: «Алгебра (логика) высказываний» (23.48 KB)
Проверочная работа по теме: «Алгебра (логика) высказываний» (23.48 KB)
 0
0 1497
1497 44
44 Нравится
0
Нравится
0


