"Производная степенной функции с натуральным показателем. Производные суммы, произведения и частного двух функций. Производная сложной функции" в условиях ДОТ

КГП на ПХВ «Павлодарский монтажный колледж» Тема урока: Производная степенной функции с натуральным показателем. Производные суммы, произведения и частного двух функций. Производная сложной функции.

Цель урока: ввести понятие производной степенной функции,сложной функции, применение правил вычисления производных в решении примеров

Производная степенной функции с натуральным показателем

Производная от  x  в степени  a  равна  a , умноженному на  x  в степени  a  минус один:

Пример

Производные суммы Чтобы найти производную суммы некоторых функций или их разности, необходимо просто воспользоваться первой теоремой производных: Производная суммы или разности некоторой функции равна сумме или разности производных: (u + v)’ = u’ + v’, (u - v)’ = u’ - v’.

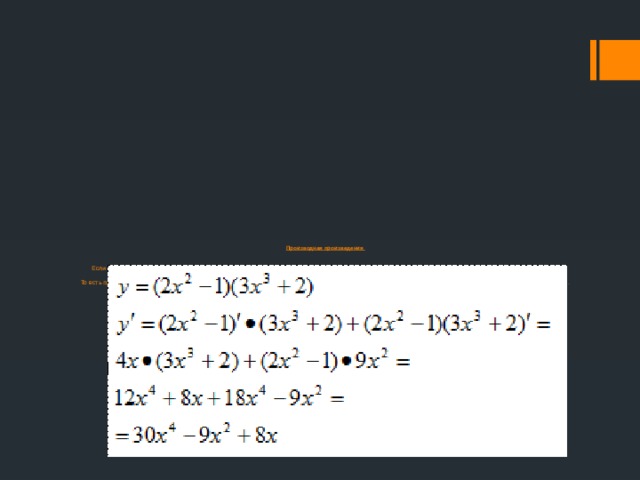
Производная произведения Если необходимо найти производную произведения или частного, то здесь уже дела обстоят посложнее, поскольку необходимо запомнить две основные формулы: (u * v)’ = u’ v + v’ u. То есть производная произведения двух некоторых функций равна сумме произведения производной первой функции на вторую и производной второй функции на первую.

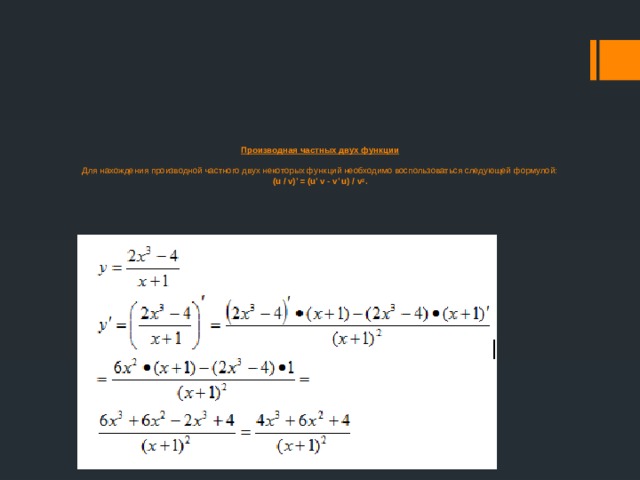
Производная частных двух функции Для нахождения производной частного двух некоторых функций необходимо воспользоваться следующей формулой: (u / v)’ = (u’ v - v’ u) / v 2 .

Производная сложной функции Производная сложной функции равна производной основной функции на производную внутренней функции