Проект на тему: «Формулы сокращенного умножения»

Выполнил ученик 7 класса

МБОУ «Черёмухинская ООШ»

Садыров Давлет

2019 г

• Изучив тему «Многочлены и действия с многочленами», меня заинтересовал вопрос, какие существуют формулы сокращенного умножения.

• Эта тема значимая в курсе математики, так как они применяются на протяжении всего периода обучения математике и используются при умножении многочленов, упрощении алгебраических выражений, сокращении дробей, разложении на множители, решении уравнений.

рассмотреть вопрос о существовании формул сокращенного умножения,

которые не рассматриваются

в школьной программе

• Познакомиться с историей возникновения формул
• Рассмотреть возведение в квадрат суммы трех слагаемых
• Изучить применение формул сокращенного умножения

• Очень давно, в Древней Греции жили и работали замечательные ученые-математики, которые всю свою жизнь отдали служению науке. В то время все алгебраические утверждения выражали в геометрической форме, вместо сложения чисел говорили о сложении отрезков, а произведение двух чисел сравнивали с площадью, трех чисел-с объемом и т.д.

Первым ученым, который отказался от геометрических способов выражения и перешел к алгебраическим уравнениям был древнегреческий ученый-математик Диофант , живший в 3 веке до нашей эры .А формулыполучили название формулы сокращенного умножения .

Диофант Александрийский

( III век н. э.) — древнегреческий математик.

(a + b)² = a² + 2ab +b² ( 1 )

(a – b)² = a² - 2ab + b² ( 2 )

(a + b)³ = a³ + 3a²b + 3ab² + b³ ( 3 )

(a –b)³ = a³ - 3a²b + 3ab² - b³ ( 4 )

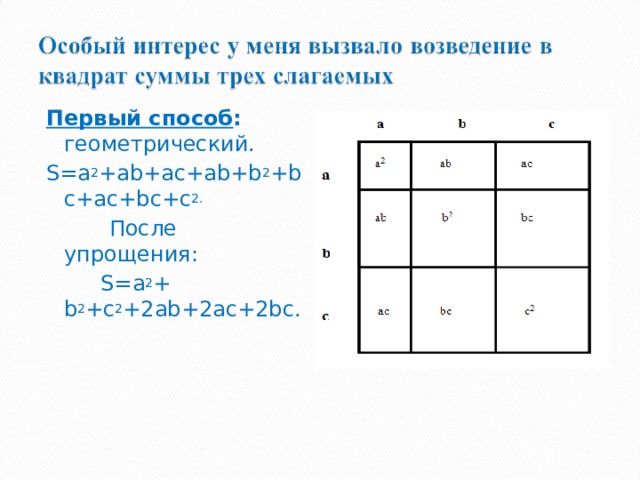
Первый способ : геометрический.

S = a 2 + ab + ac + ab + b 2 + bc + ac + bc + c 2.

После упрощения:

S=a 2 + b 2 +c 2 +2ab+2ac+2bc.

Второй способ : алгебраическое умножение многочленов.

(a+b+c)*(a+b+c)=a 2 +ab+ac+ab+b 2 +bc+ac+bc+c 2 = = a 2 + b 2 +c 2 +2ab+2ac+2bc.

Третий способ : как сумма двух слагаемых в квадрате

(( a + b )+ c ) 2 =( a + b ) 2 +2( a + b ) c + c 2 = a 2 + c 2 + b 2 +2 ab +2 ac +2 bc .

(a+b+c) 2 =a 2 +c 2 +b 2 +2ab+2ac+2bc

Я предположил, что в квадрат можно возвести сумму нескольких слагаемых. Подтверждение этому я нашёл в справочной литературе:

(a 1 + a 2 + …+ a п )² =

a 1 ²+ a 2 ²+…+2(a 1 a 2 +a 1 a 3 +…+a i a j +…+a n-1 a.)

Строки

1

1 1

  1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

1 7 21 35 35 21 7 1

• 1 1 1   1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1

Решить уравнение:

(x – 6) 2 – x(x + 8) = 2

x(x – 1) – (x – 5) 2 = 2

x 2 -12x + 36 – x 2 – 8x = 2 – 20x + 36 = 2 – 20x = 2 – 36 – 20x = – 34 x = 1,7

x 2 – x – (x 2 – 10x+25) = 2 x 2 – x – x 2 + 10x – 25 = 2 9x – 25 = 2 9x = 27 x = 3

• с 2 +4ас+а 2
• 25х 2 -10ху+у 2

Мне очень нравится предмет математика.

Она учит точности мысли, логике, умению делать обобщения.

Я считаю, что те знания, которые я приобрел, пригодятся мне в дальнейшей учебе и подготовке к выпускным экзаменам.