ПРОЕКТ
Реализация требований ФГОС ООО при обучении учащихся 8 класса
теме: «Квадратные неравенства»
Выполнил
слушатель учебного курса
«Актуальные проблемы развития профессиональной компетентности учителя математики в условиях реализации ФГОС ООО»,
учитель математики Курылева Наталья Владиславовна
МОУ « Лицей № 24 Имени Героя Советского Союза А.В. Корявина» г. Сергиев Посад.
Москва 2014
Содержание
|
|
|
| ВВЕДЕНИЕ ГЛАВА 1. Теоретические основы обучения теме § 1. Требования ФГОС ООО к школьному курсу математики. § 2. Логико-математический анализ содержания темы § 3. Цели обучения теме «Квадратные неравенства» 3.1. Развитие познавательных УУД 3.2. Развитие регулятивных УУД 3.3. Развитие коммуникативных УУД 3.4. Развитие личностных УУД ГЛАВА 2. Методические рекомендации обучения теме § 4. Карта изучения темы и её использование 4.1. Диагностируемые цели обучения теме 4.2. Логическая структура и содержание темы 4.3. Средства обучения теме (в том числе ИТ) § 5. Учебный план темы § 6. Примеры реализации целей обучения теме ЗАКЛЮЧЕНИЕ Список литературы Приложение
|
|
Введение
Актуальность. Изменение структуры образовательных стандартов происходит не только в России, но и во всем мире. Уже в середине 70-х годов прошлого века стало ясно: цикл обновления содержания образования значительно длиннее, чем цикл обновления технологий. Чтобы обучить чему-то детей, необходимо разработать методики и методические пособия, научить учителей, как ими пользоваться и как организовывать учебный процесс. На все это нужно немало времени. Но жизнь уходит вперед быстрее, и наступает момент, когда опять надо внедрять что-то новое. Поэтому педагогика встала перед необходимостью найти другие пути, обеспечивающие получение знаний в школе. В 2007 году было принято решение обозначить в стандарте не запоминаемый объем информации, а базовые требования к условиям, в которых будет проходить процесс обучения: структура образовательных программ, количество часов, отводимых на изучение предметов, во избежание перегрузки школьников материалом, требования к ключевым компетенциям, которыми они должны овладеть. Аналогичные изменения коснутся стандартов для средней и старшей школы.
Цель проекта: Реализация требований ФГОС ООО при обучении учащихся 8 класса по теме: «Квадратные уравнения»
Для достижения поставленной цели необходимо решение следующих задач.
Задачи исследования.
1. Выявить теоретические основы обучения теме, связанные с реализацией ФГОС ООО.
2. Выполнить отбор средств обучения теме, в том числе средства ИКТ
3. Разработать таблицу целей и карту обучения теме.
4. Составить учебную рабочую программу «Тематическое и почасовое планирование образовательных результатов освоения математики (в соответствии с темой).
5. Разработать методические рекомендации обучения теме и применить их в учебном процессе (фрагментов двух – трёх уроков, иллюстрирующих развитие и формирование УУД при обучении данной теме школьного курса математики).
Решение поставленных задач потребовало использования следующих методов исследования: анализ психолого-педагогической, математической и методической литературы по проблеме исследования, учебников и учебных пособий по математике; беседы с учителями, тестирование учащихся, проведение опытной проверки.
§ 1. Требования ФГОС ООО к школьному курсу математики
В чем заключается роль современной начальной школы? Интеграция, обобщение, осмысление новых знаний, увязывание их с жизненным опытом ребенка на основе формирования умения учиться. Научиться учить себя - вот та задача, в решении которой школе сегодня замены нет. В Болонской декларации 1999г. отмечается, что современные потребности учащихся останутся нереализованными, если в образовательном процессе учащийся не обретет статус субъекта образования.
Приоритетной целью школьного образования, вместо простой передачи знаний, умений и навыков от учителя к ученику, становится развитие способности ученика самостоятельно ставить учебные цели, проектировать пути их реализации, контролировать и оценивать свои достижения, иначе говоря - формирование умения учиться. Учащийся сам должен стать "архитектором и строителем" образовательного процесса. Достижение этой цели становится возможным благодаря формированию системы универсальных учебных действий (УУД) (ФГОС 2 поколения для начальной школы). Овладение универсальными учебными действиями дает учащимся возможность самостоятельного успешного усвоения новых знаний, умений и компетентностей на основе формирования умения учиться. Эта возможность обеспечивается тем, что УУД - это обобщенные действия, порождающие мотивацию к обучению и позволяющие учащимся ориентироваться в различных предметных областях познания.
Возникновение понятия «универсальные учебные действия» связано с изменением парадигмы образования: от цели усвоения знаний, умений и навыков к цели развития Личности учащегося
Универсальные учебные действия (УУД) обеспечивают способность учащегося к саморазвитию и самосовершенствованию
посредством сознательного и активного присвоения нового социального опыта это система действий учащегося, обеспечивающая: культурную идентичность, социальную компетентность, толерантность, способность к самостоятельному усвоению новых знаний и умений, включая организацию самостоятельной учебной деятельности
Функции универсальных учебных действий
1. Регуляция учебной деятельности: принятие и постановка учебных целей и задач, поиск и эффективное применение необходимых средств и способов реализации учебных целей и задач, контроль, оценка и коррекция процесса и результатов учебной деятельности
2.Создание условий для саморазвития и самореализации личности: готовность к непрерывному образованию на основе умения учиться, формирование гражданской идентичности и толерантности жизни в поликультурном обществе, развитие высокой социальной и профессиональной мобильности
3. Обеспечение успешности обучения: успешности усвоения знаний, умений и навыков; формирование целостной картины мира; формирование компетентностей в любой предметной области познания
Основания выделения УУД: цели и результаты общего образования; структурные компоненты учебной деятельности (мотив, цель, задача, учебные действия, контроль, коррекция, оценка); этапы процесса усвоения
Формы учебного сотрудничества с учителем и сверстниками
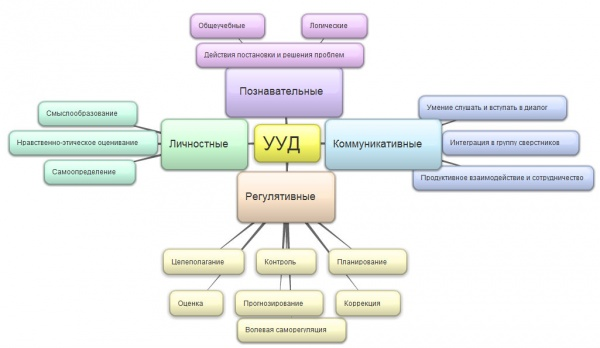
Виды универсальных учебных действий: личностные, регулятивные, общепознавательные , коммуникативные
Личностные УУД: – смыслоопределение, построение образа Я (Я-концепции), включая самоотношение и самооценку. Формирование идентичности личности, Ллчностное, профессиональное, жизненное самоопределение и построение жизненных планов во временной перспективе
Личностные УУД – смыслообразование: установление учащимся значения результатов своей деятельности для удовлетворения своих потребностей, мотивов, жизненных интересов; установление связи между целью учебной деятельности и ее мотивом - определение того «какое значение, смысл имеет для меня учение»
Личностные УУД – нравственно-этическая ориентация:
Выделение морально-этического содержания событий и действий
Построение системы нравственных ценностей как основания морального выбора
Нравственно-этическое оценивание событий и действий с точки зрения моральных норм
Ориентировка в моральной дилемме и осуществление личностного морального выбора
Виды УУД –
Регулятивные действия
Целеполагание - постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что еще неизвестно;
Планирование – определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий;
Прогнозирование – предвосхищение результата и уровня усвоения, его временных характеристик;
Контроль в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона;
Коррекция – внесение необходимых дополнений и корректив в план и способ действия в случае расхождения эталона, реального действия и его продукта;
Оценка - выделение и осознание учащимся того что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения;
Волевая саморегуляция как способность: к мобилизации сил и энергии; к волевому усилию - выбору в ситуации конфликта мотивов; к преодолению препятствий; эмоциональная устойчивость к стрессам и фрустрации; эффективные стратегии совладания с трудными жизненными ситуациями.
Общеучебные УУД
Самостоятельное выделение и формулирование учебной цели
Информационный поиск
Знаково-символические действия
Структурирование знаний
Произвольное и осознанное построение речевого высказывания (устно и письменно)
Смысловое чтение текстов различных жанров; извлечение информации в соответствии с целью чтения
Рефлексия способов и условий действия, их контроль и оценка; критичность
Выбор наиболее эффективных способов решения задач в зависимости от условий
Знаково-символические действия выполняют функции: отображения учебного материала; выделения существенного; отрыва от конкретных ситуативных значений; формирования обобщенных знаний.
Виды знаково-символических действий: замещение, кодирование/декодирование, моделирование
Познавательные УУД – логические действия
Анализ объекта с выделением существенных и несущественных признаков
Синтез как составление целого из частей, в том числе с восполнением недостающих компонентов
Выбор оснований и критериев для сравнения, классификации, сериации объектов
Подведение под понятия, выведение следствий
Установление причинно-следственных связей
Построение логической цепи рассуждения
Выдвижение гипотез, их обоснование
Доказательство
Познавательные УУД – постановка и решение проблем, формулирование проблемы,самостоятельное создание способов решения проблем творческого и поискового характера
Коммуникативные УУД: планирование учебного сотрудничества; постановку вопросов; построение речевых высказываний; лидерство и согласование действий с партнером.
УУД в системе общего образования
Формирование УУД должно выступить как цель образовательного процесса, определяя его содержание и организацию
Формирование УУД происходит в контексте усвоения разных учебных предметов
Сформированность УУД определяет эффективность учебно-воспита-тельного процесса и его результаты
Задачи
формирования УУД
1. Определить цели формирования универсальных учебных действий через описание их функций в образовательном процессе, их содержания и свойств в соотнесении с возрастно-психологическими особенностями учащихся
2. Составить ориентировочную основу каждого из УУД, обеспечивающую его успешное выполнение и организовать ориентировку учащихся в его выполнении
3. Организовать поэтапную отработку УУД, обеспечивающую переход:
от выполнения действия с опорой на материальные средства , умственной форме выполнения действия, от саморегуляции и совместного выполнения действия с учителем или, сверстниками к самостоятельному выполнению, основанному на саморегуляции.
4. Определить связи каждого УУД с предметной дисциплиной.
Выделить учебные предметы, создающие зону ближайшего развития для УУД. Определить конкретную форму УУД применительно к предметной дисциплине. Разработать системы задач для их формирования.
5. Разработать систему рекомендаций разработчикам и авторам учебников и учебных пособий по учебным предметам с целью обеспечения формирования конкретных видов и форм УУД в данной предметной дисциплине. Включить как критерий экспертной оценки учебника и учебного пособия рекомендации и учебные задания, направленные на формирование УУД.
6. Разработать учебно-методические рекомендации для педагогов.
Осуществить специальную психолого-педагогическую подготовку в рамках существующих форм повышения квалификации или профессиональной подготовки педагогов.
§ 2. Логико – математический анализ содержания темы
Тема «Квадратные неравенства» занимает важное место в математике. Эта тема связана с другими содержательными линиями: неравенства, квадратичная функция, график функции, решение неравенств.
Тема изучается в 8 классе: изучается определение квадратного неравенства, различные способы его решения.
При изучении темы имеются возможности для развития памяти, логического мышления, формирования у учащихся навыков самостоятельной работы. Квадратные неравенства сами по себе представляют интерес для изучения, так как именно с их помощью на символьном языке записываются важные задачи познания реальной действительности. Как в самой математике, так и в её приложениях с квадратными неравенствами приходится сталкиваться не менее часто, чем с уравнениями. Например, квадратные неравенства используются при изучении свойств функции (нахождение промежутков знакопостоянства функции, определение монотонности и др.)
Ожидаемые результаты – ученики должны знать определение квадратного неравенства, алгоритмов решения квадратного неравенства с помощью графика квадратичной функции и методом интервалов, уметь применять данные алгоритмы к решению задач.
Целью данной работы состоит в том, чтобы разработать методику обучения учащихся теме «Квадратные неравенства». Для реализации цели необходимо решить следующие задачи: проанализировать представление темы в различных школьных учебниках, выполнить анализ теоретического содержания темы, задачного материала темы, сделать анализ методической литературы по данной теме, разработать математического планирование, описать методику обучения теме «Квадратные неравенства», а так же описать методику обучения решению типовых задач.
Анализ представления темы в различных школьных учебниках
| Компоненты анализа учебника | Мордкович А.Г. Алгебра 8, 9 кл. | Алимов Ш.А. Алгебра 8 кл. | Никольский С.М. Алгебра 9 кл. |
| Общая структура а) характеристика частей. | 1.1. а) Материал в учебнике по данной теме разделен на 2 главы: глава 6 (в учебнике за 8 класс), которая содержит §35 и глава 1 (в учебнике за 9 класс), которая содержит §1, §2. Нумерация параграфов сквозная. Отдельно имеется задачник. Итого, содержание темы занимает три параграфа. | 1.1. а) Материал в учебнике по данной теме представлен в 4 главе «Квадратные неравенства», которая содержит 4 параграфа. Нумерация параграфов сквозная. Итого, содержание темы занимает четыре параграфа. | 1.1. а) Материал в учебнике по данной теме представлен в §2, который в свою очередь состоит из 5 пунктов. Итого, содержание темы представлено в пяти пунктах. |
| б) структура наименьшей части. | б) каждый параграф содержит только теоретический материал, примеры с подробным решением, которые являются либо опорой для введения теоретического материала, либо образцами применения теории. | б) каждый параграф содержит теоретический материал, примеры, которые являются либо опорой для введения теоретического материала, либо образцами применения теории. Имеются задания различной степени трудности. | б) каждый пункт содержит теоретический материал, который подробно объяснен на примерах. Так же имеются задания для проверки знаний и задания, предназначенные для устной работы |
| Представление задачного материала. а) классификация. | 1.2. а) задачный материал разбит на след.блоки: первый – до черты – содержит задания базового и среднего уровня сложности, к ним ответы даны в конце задачника. Второй блок упражнений – после черты – включает задания среднего и выше среднего уровня трудности. | 1.2. а) задачный материал разбит на следующие основные блоки: обязательные задачи, дополнительные более сложные задачи и трудные задачи. | 1.2. а) задачный материал разбит на следующие основные блоки: наиболее легкие задания, предназначенные для устной работы; задания повышенной трудности. |
| б) представление текста задачи. | б) задачи представлены математическим текстом. | б) в основном присутствуют задачи, представленные математическим текстом, так же есть задачи, содержащие чертеж по условию. | б) задачи представлены как стандартным математическим текстом, так и нагладно-поисковым текстом. |
| Другие структурные особенности | 1.3. При изложении материала используются различные значки типа «рабочий словарь», «вспомните», «обратите внимание» и т.д. | 1.3. При изложении материала используется разный цвет и шрифт | 1.3. Других структурных особенностей нет. |
| Методические особенности Характер изложения. | 2. 2.1. Теоретический материал рассматривается сначала на конкретных примерах, а затем делаются обобщения. Следовательно, материал учебника изложен конкретным индуктивным методом. | 2. 2.1. Теоретический материал рассматривается сначала на конкретных примерах, а затем делаются обобщения. Следовательно, материал учебника изложен конкретным индуктивным методом. | 2. 2.1. В начале вводится теоретический материал, который в последствии объясняется на примерах. Следовательно, материал учебника изложен дедуктивным методом. |
| Использование цвета, особых выделений главного. | 2.2. Материал для заучивания (определения, теоремы, правила) выделяются жирным курсивом. Алгоритмы взяты в рамочку. Номера примеров среднего уровня снабжены значком ○, номера сложных примеров - ●. | 2.2. Материал для заучивания (опред-ия, теоремы, алгоритмы) выделяются курсивом и рядом с материалом помещен розовый прямоугольник; текст, который важно знать и полезно помнить (не обязательно наизусть) помещается в рамки. | 2.2. Материал для заучивания (определения, теоремы) выделяются жирным шрифтом. ○ и ● – знаки, отмечающие начало и конец текста, необязательного при работе по обычной программе. |
| Наглядность. | 2.3. Наглядность применяется для представления и пояснения некоторых задач и теоретического материала: рисунки, чертежи. | 2.3. Имеются рисунки и чертежи для наглядного представления теоретического и задачного материала. | 2.3. Для представления и пояснения некоторых задач применяются чертежи, рисунки. |
| Повторение | 2.4. Материал для повторения не выделен. |
| Другие методические особенности. | 2.5. Нет других особенностей. |
| Выводы. Достоинства. | 3.1. Изложение материала характеризуется четкостью, алгоритмичностью, выделяются основные этапы рассуждений с фиксацией внимания читателя на выделенных этапах. | 3.1. В учебнике четко выделен материал для запоминания. Есть легкие задачи. Цветное оформление. | 3.1. В учебнике выделен текст для запоминания. Достаточно много рисунков и чертежей. |
| Недостатки. | 3.2. Задачник представлен отдельно от теорет. материала. Мало цветов. Нет исторических сведений. | 3.2. Мало рисунков и чертежей. | 3.2. Нет исторических сведений. Не используется цветное оформление. |
1. Объем содержания учебника Мордковича А.Г. по данной теме очень большой. Материал рассматривается и в 8, и в 9 классе. В учебниках Алимова Ш.А. и Никольского С.М. объем содержания примерно одинаков.
2. У Мордковича А.Г. задачный материал представлен отдельно от теоретического, что не совсем удобно. В учебнике Алимова Ш.А. присутствует и задачный, и теоретический материал. Причем теоретический материал подкреплен конкретными разобранными примерами. В учебнике Никольского С.М. мало примеров с решением, в основном теоретический и задачный материал.
3. В учебнике Мордковича А.Г. используется индуктивный метод изложения теоретического материала. Задачный материал разделен на легкие, средние задачи и задачи повышенной трудности. Цветного оформления нет, но используются различные значки для обозначения «характера» теоретического материала. У Алимова Ш.А. так же индуктивный характер изложения теоретического материала. Причем материал достаточно нагляден – присутствует большое количество рисунков, чертежей. В учебнике Никольского С.М. не используется цветовое оформление. Теоретический материал представлен дедуктивным методом. Рисунков, чертежей мало.
4. Таким образом, мой выбор – учебник Мордковича А.Г. Так как он наиболее нагляден для учащихся. Весь теоретический материал подкреплен конкретными примерами. Задачный материал рассчитан на каждого ученика: есть задачи легкого уровня, среднего и повышенной трудности.
Анализ дидактической единицы темы. С точки зрения логики:
- В теме представлено всего одно понятие – понятие квадратного неравенства, которое определено через род и видовые отличия.
- Утверждения темы сформулированы в импликативной форме.
- Алгоритма в теме два: а) алгоритм решения квадратного неравенства с помощью графика квадратичной функции; б) алгоритм решения квадратного неравенства методом интервалов.
Методы доказательства утверждений и решения задач: алгебраический; на применение алгоритма; эвристический; на построение графика. С помощью блок-схемы:
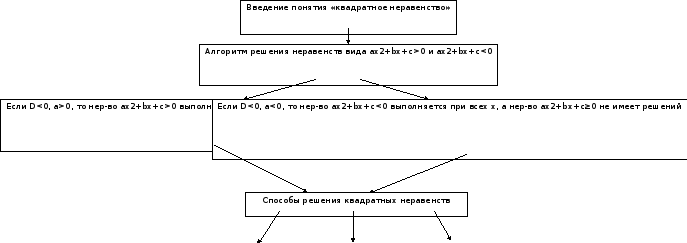
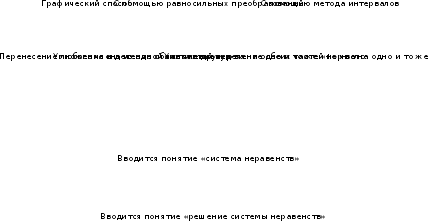
- Знать: определение квадратного неравенства, алгоритмы решения квадратного неравенства с помощью графика квадратичной функции и методом интервалов.
- Уметь: отличать квадратные неравенства от других неравенств, применять алгоритмы решения квадратных неравенств с помощью квадратичной функции и методом интервалов к решению задач.об
уАнализ теоретического содержания темы
Анализ понятий.
В теме представлено 2 понятия, из которых только одно определено явно.
Формулировка определения понятия: Если в левой части неравенства стоит квадратный трехчлен, а в правой – нуль, то такое неравенство называют квадратным.
Логический анализ структуры определения понятия «квадратное неравенство»:
- термин – квадратное неравенство;
- род – неравенство;
- видовые отличия: в левой части неравенства стоит квадратный трехчлен, а в правой – нуль;
- связь между видовыми отличиями –с точки зрения логики – импликативное определение;
- вид определения – через род и видовые отличия;
- опорные знания – понятие неравенства, понятие квадратного трехчлена.
Подведение под понятие (примеры конкретных квадратных неравенств и контрпримеры):
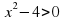 ;
; 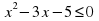 ;
; 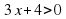 ;
; 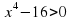 ;
;
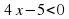 .
.
Следствия из определения понятия: решение квадратного неравенства (графическим методом, аналитическим методом, методом интервалов).
Возможные ошибки в формулировке определения: учащиеся вместо двух существенных признаков называют только один; забывают указать слово «неравенства».
Используется импликативная связь между видовыми отличиями в определении понятия. Понятие определяется через род и видовые отличия. Подведение под понятие осуществляется с помощью примеров конкретных квадратных неравенств и контрпримеров. Опорными знаниями являются понятия неравенства и квадратного трехчлена. Возможные ошибки состоят в том, что учащиеся вместо двух существенных могут назвать только один, забывают указать слово «неравенства».
Анализ утверждений.
I.
Формулировка утверждения: Если D совпадает со знаком числа а.
Структура утверждения:
- разъяснительная часть – любая квадратичная функция;
- условие – 1) D;
- заключение - При всех действительных значениях х знак квадратичной функции 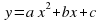 совпадает со знаком числа а.
совпадает со знаком числа а.
3. Форма формулировки утверждения – импликативная.
4. Вид утверждения – сложное (два условия, одно заключение).
5. Метод доказательства – алгебраический.
6. Достаточное или необходимое условие – достаточное.
7. Опорные знания: понятие дискриминанта, понятие квадратного трехчлена, понятие действительного числа.
8. Возможные ошибки и затруднения: в формулировке утверждения пропускают слово «действительных».
II.
Формулировка утверждения: Если D=0, то при всех действительных значениях х, кроме 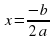 , знак квадратичной функции
, знак квадратичной функции 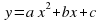 совпадает со знаком числа а; при
совпадает со знаком числа а; при 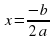 значение квадратичной функции равно нулю.
значение квадратичной функции равно нулю.
Структура утверждения:
- разъяснительная часть – любая квадратичная функция;
- условие – 1) D=0; 2) 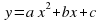 ;
;
- заключение – 1) при всех действительных значениях х, кроме 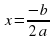 , знак квадратичной функции
, знак квадратичной функции 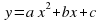 совпадает со знаком числа а; 2) при
совпадает со знаком числа а; 2) при 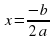 значение квадратичной функции равно нулю.
значение квадратичной функции равно нулю.
Форма формулировки утверждения – импликативная.
Вид утверждения – сложное (два условия, два заключения).
Метод доказательства – алгебраический.
Достаточное или необходимое условие – достаточное.
Опорные знания: понятие дискриминанта, понятие квадратного трехчлена, понятие действительного числа.
Возможные ошибки и затруднения: в формулировке утверждения пропускают слово «действительных».
III.
Формулировка утверждения: Если D0, то знак квадратичной функции 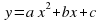 совпадает со знаком числа а для всех х, лежащих вне отрезка [x1,x2], т.е. при xx1 и при xx2, где x1x2 – нули функции; знак квадратичной функции противоположен знаку числа а при x1xx2.
совпадает со знаком числа а для всех х, лежащих вне отрезка [x1,x2], т.е. при xx1 и при xx2, где x1x2 – нули функции; знак квадратичной функции противоположен знаку числа а при x1xx2.
Структура утверждения:
- разъяснительная часть – любая квадратичная функция;
- условие – 1) D0; 2) 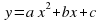 ;
;
- заключение – 1) знак квадратичной функции 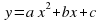 совпадает со знаком числа а для всех х, лежащих вне отрезка [x1,x2], 2) знак квадратичной функции противоположен знаку числа а при x1xx2.
совпадает со знаком числа а для всех х, лежащих вне отрезка [x1,x2], 2) знак квадратичной функции противоположен знаку числа а при x1xx2.
Форма формулировки утверждения – импликативная.
Вид утверждения – сложное (два условия, два заключения).
Метод доказательства – алгебраический.
Достаточное или необходимое условие – достаточное.
Опорные знания: понятие дискриминанта, понятие квадратного трехчлена, понятие действительного числа.
Возможные ошибки и затруднения: в формулировке утверждения забывают указывать значения х.
Все утверждения даны в импликативной форме. Все теоремы сложные. Во всех теоремах используется алгебраический метод доказательства. Данные теоремы являются достаточными условиями. Опорными знаниями являются понятия дискриминанта, квадратного трехчлена, действительного числа. Возможные ошибки состоят в том, что учащиеся могут забыть в формулировке теорем указывать значения x, пропускать слово «действительных».
Анализ алгоритмов (правил)
В данной теме содержатся два алгоритма: алгоритм решения квадратного неравенства с помощью графика квадратичной функции и алгоритм решения квадратного неравенства методом интервалов.
I. Алгоритм решения квадратного неравенства с помощью графика квадратичной функции:
1) определить направление ветвей параболы по знаку первого коэффициента квадратичной функции;
2) найти действительные корни соответствующего квадратного уравнения или установить, что их нет;
3) построить эскиз графика квадратичной функции, используя точки пересечения (или касания) с осью Ох, если они есть;
4) по графику определить промежутки, на которых функция принимает нужные значения.
| Правило | Корректировка правила | Обосновывающ. знания | Опорные знания |
| 1. а) если а б) если a0, то ветви параболы направлены вверх. 2. а) если сущ. х1 и х2 - корни квадратного трехчлена, то график имеет две точки пересечения с осью Ох; б) если сущ. только х1, то график имеет одну точку пересечения с осью Ох; в) если корней нет, то пересечения графика с осью Ох нет. 3. Эскиз графика квадр. функции. 4. Записать ответ. | Расписать правило на 4: 1. ax2+bx+c0; 2. ax2+bx+c 3. ax2+bx+c≤0; 4. ax2+bx+c≥0; | Сравнение чисел с нулем, нахождение корней квадратного трехчлена. | Сравнение чисел с нулем, нахождение корней квадратного трехчлена, тождественные преобразования неравенств. |
II. Алгоритм решения квадратного неравенства методом интервалов:
1) Найти корни квадратного трехчлена;
2) Отметить данные корни на числовой оси;
3) Определить знак квадратного трехчлена на каждом из полученных интервалов;
4) Выбрать требуемые промежутки и записать ответ.
| Правило | Корректировка правила | Обосновывающ. знания | Опорные знания |
| 1. Найти корни ax2+bx+c=0; 2. Отметить данные корни на числовой оси; 3. Определить промежутки на которых ax2+bx+c0 и ax2+bx+c 4. Записать ответ. | Расписать правило на 4: 1. ax2+bx+c0; 2. ax2+bx+c 3. ax2+bx+c≤0; 4. ax2+bx+c≥0; | Сравнение чисел с нулем, нахождение корней квадратного трехчлена. | Сравнение чисел с нулем, нахождение корней квадратного трехчлена, тождественные преобразования неравенств. |
«Ядерным» материалом темы являются одно новое понятие, три утверждения и два алгоритма;
Теоретический материал изложен индуктивно;
Задачный материал способствует отработке представленной теории на 1 и 2 УУ
§ 3. Цели обучения теме « Квадратные неравенства».
Для чего нужна таблица целей:
Чтобы обучение было открытое, учащиеся могли знать уровни обучения и сами выбирать уровень обучения;
Для оценивание учащихся. Ученик выбирает уровень на «5», на «4», на «3»;
Для того чтобы учащийся планировал свою деятельность.
Таблица целей обучения теме «Квадратные неравенства и их решение»
| Формулировки обобщённых целей | Формулировки учебных задач, с помощью которых достигается обобщённая цель | Опознаваемость целей |
| цель считается достигнутой, если ученик: |
| первом | втором | третьем |
| Ц1: приобретение УИ, формирование логических ПУД | а) сравнивает уравнения по заданному признаку: неизвестная входит под знак корня и составляете схему определения понятия «Неравенства» с использованием учебника и набора упражнений; в) сравнивает решение однотипных неравенств 1-го уровня сложности | а) составляет схему определения понятия «Неравенства» с использованием набора объектов; б) выполняет анализ и выявляет преобразования, нужные для решения неравенств, с использованием помощи; обобщаете решение неравенств одного типа | а) даёт определение типов неравенств, дополняет классификацию типов неравенств; б) выполняет анализ и выявляете преобразования, нужные для решения неравенств, в) составляете приёмы решения неравенств данного типа с помощью указаний | а) общая схема определения понятия; б) классификации типов выражений, функций, уравнений и неравенств. |
| Ц 2: кон-троль усвоения теории;
| знает: а) определения неравенства, классификацию и определение типов неравенств; б) стандарты неравенства каждого типа и их решение; в) преобразования групп «А», «В», «С»; г) способы выполнения проверки; д) метод интервалов; е) приемы графического решения неравенств; ж) прием решения текстовых задач; з) способы раскрытия модуля; и) прием анализа вида выражения; к) приемы саморегуляции; л) мировоззренческое значение неравенств | информационные схемы, карточки- информаторы |
| Ц3: применение знаний и умений | первом | втором | третьем | прием саморегуляции, предписания, стандарты неравенств, и их решений |
| умеет: а) использовать основные преобразования для решения простейших неравенств в соответствии со стандартами; б) решать простейшие текстовые задачи с использованием ориентиров | умеет: а) использовать все преобразования и способы для решения неравенств 2-го уровня сложности; б) метод интервалов – для решения неравенств; в) решать текстовые задачи 2-го уровня сложности | умеет а) использовать все преобразования и способы для решения неравенств 3-го уровня сложности; б) метод интервалов – для решения неравенств; в) решать текстовые задачи 3-го уровня сложности; г) использовать эвристики для решения неравенств |
| Ц4: формирование КУД | на своем уровне освоения темы: а) работает в группе, оказывает взаимопомощь, рецензирует ответы товарищей; б) организует взаимоконтроль, взаимопроверку и др. на всех этапах учебно-познавательной деятельности (УПД) по выполненным заданиям предыдущих уровней с обоснованием; в) оказывает помощь, работающим на предыдущих уровнях; г) осуществляет поиск информации для подготовки письменного сообщения и устного выступления в соответствии с изучаемой темой, используя правила коммуникативного взаимодействия | приёмы контроля, оценки; таблица коммуникативной компетентности |
| Ц5: формирование общих ПУД и РУД | В соответствии со своим уровнем освоения темы: а)сам выбирает уровень достижения целей и формулируете цели своей учебной деятельности; б) выбирает темы для дополнительного изучения; в) формулирует цели своей деятельности; г) осуществляете самопроверку с использованием образцов, приёмов; д) оцениваете свою итоговую деятельность по данным объективным критериям; по собственным критериям, сравнивая их с объективными критериями; е) делаете выводы о дальнейших действиях, планирует коррекцию учебно-познавательной деятельности | приёмы саморегуляции УПД |
УИ - учебная информация; ПУД – познавательные; КУД – коммуникативные; РУД – регулятивные учебные действия
ГЛАВА 2. Методические рекомендации обучения теме
§ 4. Карта изучения темы и её использование
На основании составленной карты целей и учебных задач разрабатывается карта соответствующей темы. Эта карта позволяет ученику: выбрать уровень усвоения темы, дополнительный материал для самостоятельного изучения по теме, определить цели и средства освоения темы.
Карта изучения темы «Квадратные неравенства»
| I. Логическая структура и цели изучения темы (таблица целей) |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Ц 1,5 | Ц 2 -5 | Ц 1-2 | Ц 2-4 | Ц 2- 4 | Ц 1,5 | Ц 2-4 | Ц1,5 | Ц 2-4 | Ц 2-4 | Ц 2 - 4 | Ц2, 3, 4,5 |
| П. 31 | П. 31 | П.32
| П. 32 | П. 32 | П. 33 | П. 33 | П.34 | П.34 | П.34 Подготовка к К.р. | Контрольная работа № 8по теме : «Неравенства» | Урок коррекции |
| II. Блок актуализации знаний учащихся |
| Знать: Свойства и график изученных функции, числовые промежутки Уметь: решать линейные, квадратные уравнения, строить гафики изученных элементарных функций |
| III. Предметные результаты (Ц 2, 3 таблицы целей): уметь решать линейные неравенства, квадратные неравенства используя понятия; способы графический способ решения квадратных неравенств. |
| YI. Образцы заданий итоговой контрольной работы (Ц 5) | Y. Средства обучения теме |
| 1 уровень | Баллы | 2 уровень | Баллы | 3 уровень | Баллы |
|
| 1.Решите неравенство: а)5(3-х)˂2(4х+1); б)22х+15-5х2≥0. 2.Решите уравнение: а)3√х-8=3/√х; б)√2х+29= х-3. 3.Найдите область определения выражения√4х-х2. | 1
1
1 | 1. Решите неравенство: а)3(4х-1)≥-5(5+2х); б) х+35-6х2≤0. 2. Решите уравнение: а) 5√х – 5/√х = 24; б) √44 - х = х - 2. 3. Найдите область определения выражения √(х2+ 6х)-1. 4. Докажите, что функция у = - 6/х + 4 возрастает при х˃0. | 1
1
1
1
| 1.Решите неравенство: а) 22х + 5≤ 3(6х – 1); б) х2 – 11х + 24˂0. 2. Решите уравнение: а) 5х - 18√х – 8 = 0; б) √33 -8х = х. 3. Найдите область определения выражения √2 – 5х. 4. Докажите , что функция у=4 – 2х убывает. 5 5. при каких значениях параметра р уравнение х2 + 2рх – 7р = 0. | 1
1 1 1
1
| 1)приём решения неравенств: способом алгебраических преобразований; графическим способом; 2) мнемоническое правило для запоминания приема; 3) эвристические рекомендации для решения неравенств искусственным способом; 4) приёмы саморегуляции при выполнении преобразований и решении неравенств |
| YI. Задания для внеаудиторной самостоятельной работы (Ц 2, 3, 5) |
| 1 уровень (обязательный уровень стандарта): №№31.2, 31.4, 31.9, 31.11, 32.2, 32.3, 32.9, 32.6, 32.7, 33.2, 33.3,33.4, 33.6, 33.14, 34.1, 34.2, 33.4, .5, 34. 15,34. 28, 34. 37. |
| 2 уровень: №№ 31. 3, 31.6, 31.8, 31.12, 31,14, 31.17, 31.20, 31.22, 31.24, 31.33, 32.2, 32.3, 32.9, 32.6, 32.7, 33.2, 33.3,33.4, 33.6, 33.14, 34.1, 34.2, 33.4, .5, 34. 15,34. 28, 34. 37. |
| 3 уровень: №№31.25, 31.28, 31.30, 31.31, 31.32, 31.36, 31.38, 31.40, 31.42,31.421,31.43, 31.44,32.4, 32.5, 33.35, 33.36, 33.37,34.21, 34.22, 34.25, 34,26,34.27. |
| 4 уровень: №№ (со звёздочкой) 31.50, 31.51, 31.57,31.58, 31.60, 31.61, 31.62, 32.63,31.64, 31.65,31.32.4,32.5, 32.8, 33.35, 33.36, 33.38.33.37,33.38, 34.25,34.26,34.27,34.43,34.46, |
| YII. Темы индивидуальных заданий (Ц 5) |
Работа индийского математика и астронома Ариабхатты. . 2) Работа индийского ученого Брахмагупта (VII в). 3) Квадратные уравнения умели решать около 2000 лет до нашей веры вавилоняне. 4) Диофант Александрийский. 5) Сообщение ученика о Мухаммеде аль-Хорезми. 7) Самостоятельно выбранная тема.
|
| YIII. Метапредметные результаты: перечень учебных действий (умений) для освоения темы (Ц 1 - 5) |
| Познавательные УУД | Регулятивные УУД | Коммуникативные УУД | Личностные УУД |
| Сравнение, обобщение, конкретизация, анализ; составление схемы определения понятия, подведение под понятие; постановка и решение проблемы при составлении задачи | Выбор и принятие целей, составление плана, самоконтроль, самооценка, соотнесение своих знаний с той учебной информацией, которую нужно усвоить; приёмы саморегуляции | Взаимоконтроль, взаимопроверка, распределение обязанностей в группе, умение слушать, выступать, рецензировать, писать текст выступлений | Рефлексия собственной деятельности |
§ 5. Учебный план темы
Примерная форма примерной рабочей учебной программы по математике (фрагмент)
Утверждаю Согласовано Рассмотрено
Директор МОУ № __ Зам. директора по УВР на заседании ШМО
__________ Ф.И.О. _____________ Ф.И.О. протокол № ________
от ________________
Руководитель ШМО
___________ Ф.И.О.
Тематическое и почасовое планирование образовательных результатов освоения математики
на 2011/2012 учебный год (фрагмент)
Класс: _8__
Учитель: _Курылева Н.В.
Количество часов: на учебный год: ___102_в неделю:__3_
Плановых контрольных уроков: : I ч. – 2 ; II ч. – 2 ; III ч. – 2; IV ч. – 2;
Планирование составлено на основе источников:
1) Примерное тематическое планирование к учебнику Алгебра 8 кл. http://www.shevkin.ru
2) Учебник Алгебра 8, А.Г. Мордкович .
4) Методические рекомендации: http://www.shevkin.ru
5) Дидактические материалы: http://www.shevkin.ru
6) Примерные программы по учебным предметам. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала анализа. 10-11 классы / авт.- сост. И.И.Зубарева, А.Г. мордкович. – М. : Мнемозина, 2007.- 64 с.
7) Боженкова Л.И. Алгебра в схемах, таблицах, алгоритмах: Учебные материалы. Калуга: КГПУ, 2012.
Тематическое планирование составил: Курылева Н.В. Дата 2012 Подпись _____________
Условные обозначения: ПУУД – познавательные УУД; ПЛ УУД - познавательные логические УУД; ПО УУД - познавательные общеучебные УУД; РУУД – регулятивные УУД; КсУУД – коммуникативные УУД сотрудничество; КрУУД – коммуникативные УУД для общения: развитие устной и письменной речи; Ц1 – Ц 5 – цель 1 – 5; ДЗ – домашнее задание; УПД – учебно-познавательная деятельность.
| № уро- ков | Раздел, тема урока | Форма урока; форма обучения | Предметные и метапредметные результаты Ц 1 (ПЛ УУД), Ц 2 (ПО УУД, РУУД), Ц 3 , Ц 4 (КсУУД, КРУУД), Ц 5 (ПОУУД, РУУД) |
| 1 - 12 | Название темы Квадратные неравенства Средства обучения 1) таблицы….. 2) подсказки к поиску решения задач; 3) предписания… 4) карточки с приёмами; 5) Карта темы | Уроки: семинар, практикум, лекция, др. Фронтальная, индивидуальная групповая формы обучения | Ц 1: приобретение учебной информации и развитие интеллектуальных умений при изучении: а) понятий; б) теорем; в) типов задач Ц 2: контроль усвоения теоретических знаний: а) математических понятий; б) теорем; в) типов и классов задач Ц 3: применение знаний и интеллектуальных умений при решении математических и учебных задач Ц 4: развитие коммуникативных умений через: включение в групповую работу; взаимопомощь, рецензирование ответов; организацию взаимоконтроля и взаимопроверки на всех этапах УПД Ц 5: развитие организационных умений (целеполагание, планирование, реализация плана, саморегуляция УПД |
|
|
| 1 | Свойства числовых неравенств, п. 31
| Инструктивная лекция Урок смешанного типа Фронтально-индивидуальная | Ц 5: Введение в тему, постановка и формулирование целей своей учебной деятельности; Ц 1: Развитие познавательных логических УУД
|
| 2 | Свойства числовых неравенств, п. 31
| Практикум: Фронтальная и парная формы | Ц 2: а1) указывает признаки понятий: …………….. б1) перечисляет: основные понятия и отношения между ними, свойства; переходит от одной модели к другой; в 1) выполняет ……; в 2) перечисляет …, применяет их к решению задач; Ц 3, Ц 4, Ц 5 |
| 3 | Исследование функций на монотонность, п. 32
| Лекция – диалог Фронтально-индивидуальная работа
| Постановка и решение проблемы (познавательные УУД) Ц 1: составление плана и схем поиска доказательства, решения задачи ….; составление предписаний; Ц 2: контроль усвоения изученного материала в процессе чтения лекции Ц 4 (КрУУД): запись лекции; ПОУУД – построение речевых высказываний, посредством смыслового разделения текста на части и подбор заголовка к фрагменту лекции; составление плана лекции. |
| 4 | Исследование функций на монотонность, п. 32 | Практикум: Парное взаимообучение | Ц 2: находит ошибки в решении задач своего уровня сложности; решает задачи своего уровня сложности; Ц 4: |
| 5 | Исследование функций на монотонность, п. 32
| Практикум Фронтально-индивидуальная, индивидуальная или парная | Ц 2, 3: использует предписания для решения типов задач своего уровня сложности, составляет задачи, аналогичные данным, обратные задачи и решает их; Ц 4: в соответствии таблицей целей;
|
| 6 | Решение линейных неравенств, п. 33 | Инструктивная лекция Урок смешанного типа Фронтально-индивидуальная | Ц 5: Введение в тему, постановка и формулирование целей своей учебной деятельности; Ц 1: Развитие познавательных логических УУД
|
| 7 | Решение линейных неравенств, п. 33 | Практикум: Парное взаимообучение
| Ц 2: находит ошибки в решении задач своего уровня сложности; решает задачи своего уровня сложности; Ц 4: |
| 8 | Решение квадратных неравенств, п.34 | Лекция – диалог Фронтально-индивидуальная работа
| Постановка и решение проблемы (познавательные УУД) Ц 1: составление плана и схем поиска доказательства, решения задачи ….; составление предписаний; Ц 2: контроль усвоения изученного материала в процессе чтения лекции Ц 4 (КрУУД): запись лекции; ПОУУД – построение речевых высказываний, посредством смыслового разделения текста на части и подбор заголовка к фрагменту лекции; составление плана лекции. Ц5 в соответствии таблицей целей (в качестве ДЗ); |
| 9 | Решение квадратных неравенств, п.34 | Практикум | Ц 2, 3: использует предписания для решения типов задач своего уровня сложности, составляет задачи, аналогичные данным, обратные задачи и решает их; Ц 4: в соответствии таблицей целей;
|
| 10
| Решение квадратных неравенств, п.34 | Практикум | Ц 2, 3: использует предписания для решения типов задач своего уровня сложности, составляет задачи, аналогичные данным, обратные задачи и решает их; Ц 4: в соответствии таблицей целей;
|
| 11 | Контрольная работа № 8 по теме: « Неравенства». | Практикум. Индивидуальная | Ц 2, 3, 4ё: выбирает задачи своего уровня сложности , решает их, осуществляет самопроверку; делает выводы о качестве собственных знаний, необходимых для выполнения контрольной работы |
| 12 | Урок коррекции и рефлексии | Рефлексивный семинар Индивидуальная, парная (взаимопомощь) | Ц 2, Ц 4: анализирует собственные ошибки с помощью товарища и исправляет их; Ц 5: ( в соответствии с таблицей целей): вспоминает планируемые цели своей учебной деятельности; е) делает выводы о результатах своей деятельности; планирует коррекцию учебной познавательной деятельности |
| Внеурочная самостоятельная деятельность: |
| I. Тематика для подготовки рефератов, выступлений на конференцию, математический вечер, декаду математики и др. (по итогам изучения темы, курса за четверть, за 1-е полугодие, за год) 1) Работа индийского математика и астронома Ариабхатты. 2) Работа индийского ученого Брахмагупта (VII в). 3) Квадратные уравнения умели решать около 2000 лет до нашей веры вавилоняне. 4) Диофант Александрийский. 5) Сообщение ученика о Мухаммеде аль-Хорезми. 6) Самостоятельно выбранная тема. 1. II. Тематика долгосрочных проектов по разделу 1) Решение неравенств в целых числах. 2) Решение квадратных неравенств.. |
§ 6. Примеры реализации целей обучения теме
Урок 8: «Квадратное неравенство».
Предмет, класс, количество часов: Алгебра, 8 класс, 1 час.
Тип урока: урок изучения нового.
Цели урока:
ОЦ: Обеспечить усвоение понятия «квадратное неравенство».
ВЦ: Формирование у учащихся навыков самостоятельной работы.
РЦ: Развитие умений анализировать, сравнивать, конкретизировать и делать выводы.
Методы обучения: объяснительно-иллюстративный, частично-поисковый, репродуктивный.
План урока
Оргмомент.
Актуализация знаний.
Введение понятия «квадратное неравенство».
Отработка новых знаний.
Подведение итогов урока.
Постановка домашнего задания.
ХОД УРОКА
Оргмомент.
Ребята, сегодня мы начинаем изучать новую главу «Квадратные неравенства». На сегодняшнем уроке мы с вами постараемся узнать, что же такое квадратное неравенство.
Актуализация знаний.
Для начала давайте вспомним, что вообще мы понимаем под неравенством. (дети говорят, что число а больше числа b, если разность a-b положительна. Число а меньше числа b, если разность a-b отрицательна).
Хорошо. Мы с вами знаем линейные неравенства, которые содержат линейные функции. Скажите, а какую функцию мы называли квадратичной? (Функция 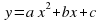 , где a,b и c заданные действительные числа, a≠0, х – действительная переменная, называется квадратичной функцией).
, где a,b и c заданные действительные числа, a≠0, х – действительная переменная, называется квадратичной функцией).
Укажите среди записанных на доске функций квадратичную.
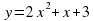 ;
; 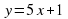 ;
; 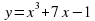 ;
;  .
.
(Квадратичными являются первая и последняя функции. Во втором случае функция является линейной, а в третьем – кубической).
Введение понятия «квадратное неравенство».
Ребята, на доске вы видите записи
 ,
,  ,
,  ,
,  ,
,
 ,
,  .
.
Какие из данных неравенств являются линейными?
(Линейными являются неравенства .
Почему вы сделали такие выводы?
(Потому что данные неравенства содержат линейные функции)
Хорошо! Какие еще неравенства вы видите на доске?
(Неравенства .
Молодцы. У нас остались еще два неравенства, которым мы ни как не можем дать названия.
Посмотрите, какие функции стоят в левой части оставшихся неравенств?
(В левой части оставшихся неравенств стоят квадратичные функции).
Правильно! Итак, ребята, если мы с вами вспомним сейчас все, что говорили чуть ранее, какой вывод мы с вами можем сделать? Какие неравенства мы будем называть квадратными?
(Если в левой части неравенства стоит квадратичная функция, то такое неравенство называют квадратным).
Хорошо… Только вы забыли сказать про левую часть неравенства. Что стоит в ней?
(В левой части такого неравенства стоит ноль!)
Молодцы! Значит, если в левой части неравенства стоит квадратный трехчлен, а в правой – нуль, то такое неравенство называют квадратным.
Отработка новых знаний.
Хорошо, ребята, давайте теперь проверим насколько вы усвоили данный материал.
Укажите какие из следующих неравенств являются квадратными:
1) 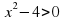 ; 2)
; 2) 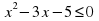 ; 3)
; 3)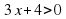 ;
;
4) 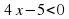 ; 5)
; 5)  ; 6)
; 6) 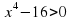 .
.
(Квадратными неравенствами являются неравенства под цифрами 1), 2) и 5)).
Почему вы сделали такой вывод?
(Т.к. в левой части этих неравенств стоят квадратные трехчлены, а в правой части стоит ноль!).
Хорошо. Давайте теперь вы сами выйдете к доске и приведете примеры квадратных неравенств.
(Ребята по очереди выходят к доске и записывают примеры квадратных неравенств).
Молодцы. Но ведь неравенства могут быть даны не в явном виде. Попробуйте свести к квадратным следующие неравенства:
 ;
;  ;
;  ;
;
.
( 1)  . Перенесем выражение, стоящее в правой части неравенства, в левую часть данного неравенства. При этом поменяем знаки:
. Перенесем выражение, стоящее в правой части неравенства, в левую часть данного неравенства. При этом поменяем знаки:  . Данное неравенство является квадратным, т.к. удовлетворяет нашему определению.
. Данное неравенство является квадратным, т.к. удовлетворяет нашему определению.
2) . Поступим так же, как и в предыдущем примере:
. Поступим так же, как и в предыдущем примере:  . Данное неравенство так же является квадратным.
. Данное неравенство так же является квадратным.
3)  . Перенесем квадратный трехчлен из правой части неравенства в левую:
. Перенесем квадратный трехчлен из правой части неравенства в левую:  . Приведем подобные:
. Приведем подобные:  . Данное неравенство является квадратным.
. Данное неравенство является квадратным.
4)  . Так же переносим выражение, стоящее в правой части неравенства, в левую: . Раскроем скобки и приведем подобные:
. Так же переносим выражение, стоящее в правой части неравенства, в левую: . Раскроем скобки и приведем подобные:  ;
;  . Данное неравенство является квадратным.)
. Данное неравенство является квадратным.)
Подведение итогов урока.
Итак, давайте подведем итоги.
С каким новым понятием мы сегодня познакомились?
(С понятием квадратного неравенства).
Какое неравенство мы с вами называем квадратным?
(Если в левой части неравенства стоит квадратный трехчлен, а в правой – нуль, то такое неравенство называют квадратным).
Постановка домашнего задания.
Почитайте §34, стр 200. Определение наизусть.
№ 34.1,№ 34.3, № 34.5.
Урок 9: «Решение квадратного неравенства с помощью графика квадратичной функции»
Предмет, класс, количество часов: Алгебра, 8 класс, 1 час.
Тип урока: урок изучения нового.
Цели:
ОЦ: Обеспечить усвоение алгоритма решения квадратного неравенства с помощью графика квадратичной функции.
ВЦ: Формирование у учащихся навыков самостоятельной работы, воспитание сообразительности, воспитание аккуратности.
РЦ: развитие умений анализировать, конкретизировать и делать выводы; развитие памяти через неоднократное повторение.
Методы обучения: объяснительно-иллюстративный, частично-поисковый, репродуктивный.
План урока
Оргмомент.
Проверка домашнего задания.
Актуализация знаний.
Введение алгоритма решения квадратного неравенства с помощью графика квадратичной функции.
Отработка новых знаний.
Подведение итогов.
Постановка домашнего задания.
ХОД УРОКА
Оргмомент.
Сегодня мы продолжаем изучать главу «Квадратные неравенства». На сегодняшнем уроке мы познакомимся с алгоритмом решения квадратного неравенства с помощью графика квадратичной функции и постараемся решить несколько задач.
Проверка домашнего задания.
Для начала давайте посмотрим что было задано вам на дом и проверим как вы справились с заданием.
(На дом был задан § 34 и№ 34.1,№ 34.3, № 34.5).
Откройте тетрадки, я пройду, посмотрю ваши решения.
Актуализация знаний.
Что значит решить неравенство?
(Решить квадратное неравенство – это значит найти множество всех х, для которых данное неравенство выполняется или доказать, что таких х нет).
Какие ответы могут получиться при решении квадратного неравенства?
(При решении квадратного неравенства могут быть четыре случая:
1) Решений может не быть, 2) решением может быть вся числовая ось, 3) решением является объединение промежутков, содержащих знаки бесконечности, 4) решением может быть числовой промежуток.)
В чем «проявляется» каждый коэффициент квадратичной функции на ее графике?
(Коэффициент а влияет на направление ветвей параболы; коэффициент с показывает на то, пересекает ли график ось Оу; коэффициенты а и b участвуют в вычислении вершины; так же все коэффициенты участвуют в вычислении дискриминанта, который влияет на наличие корней).
Ребята, на доске вы видите четыре чертежа.
Докажите, что на чертеже изображено решение данного неравенства.
(Учащиеся выходят к доске и, рассматривая каждое неравенство, доказывают, что на графике изображено его решение.
Так, на графике 1 изображено решение неравенства  . Т.к. старший коэффициент а=20 = ветви параболы направлены вверх. Дискриминант больше нуля, следовательно, существует два корня – две точки пересечения с осью Ох.
. Т.к. старший коэффициент а=20 = ветви параболы направлены вверх. Дискриминант больше нуля, следовательно, существует два корня – две точки пересечения с осью Ох.
На графике 2 изображено решение неравенства  . Т.к. дискриминант меньше нуля, следовательно, пересечения графика с осью Ох нет. Старший коэффициент а=20, следовательно, ветви параболы направлены вверх.
. Т.к. дискриминант меньше нуля, следовательно, пересечения графика с осью Ох нет. Старший коэффициент а=20, следовательно, ветви параболы направлены вверх.
На графике 3 изображено решение неравенства  . Т.к. старший коэффициент а=-1
. Т.к. старший коэффициент а=-1
На графике 4 изображено решение неравенства  . Старший коэффициент а =10, следовательно, ветви параболы направлены вверх. Дискриминант равен нулю, следовательно одна точка пересечения графика с осью Ох).
. Старший коэффициент а =10, следовательно, ветви параболы направлены вверх. Дискриминант равен нулю, следовательно одна точка пересечения графика с осью Ох).
Молодцы, ребята!
Введение алгоритма решения квадратного неравенства с помощью графика квадратичной функции
Давайте рассмотрим несколько примеров.
1. Решить неравенство  .
.
Найдем дискриминант этого квадратного трехчлена. Имеем
, т.е. пересечения графика с осью Ох нет.
Старший коэффициент трехчлена (число 2) положителен, следовательно, ветви параболы направлены вверх.
Схематически график уравнения  имеет вид:
имеет вид:
Мы видим, что весь график данной функции лежит выше оси Ох, т.е. все значения положительны. Следовательно, неравенство  имеет решение на всей числовой прямой (-∞, +∞).
имеет решение на всей числовой прямой (-∞, +∞).
Рассмотрим второй случай:
Пусть требуется решить неравенство  .
.
Найдем дискриминант квадратного трехчлена. Имеем т.е. пересечения графика с осью Ох нет. Старший коэффициент трехчлена (число -1) отрицателен, т.е. ветви параболы направлены вниз.
Схематически график уравнения  имеет вид:
имеет вид:
Мы видим, что график данной функции лежит ниже оси Ох, т.е. все значения отрицательны. Следовательно, неравенство  не выполняется ни при каком значении х, т.е. неравенство не имеет решений.
не выполняется ни при каком значении х, т.е. неравенство не имеет решений.
Теперь давайте попробуем сформулировать алгоритм решения квадратного неравенства с помощью графика квадратичной функции.
(Ученики пытаются сформулировать алгоритм, делая опору на решенные примеры).
Хорошо ребята, давайте теперь все вместе проговорим этот алгоритм:
1. Найти корни квадратного трехчлена ax2+bx+c.
2. Найти знак старшего коэффициента и с учетом этого определить направление ветвей параболы.
3. Построить схематический график трехчлена.
4. С помощью полученной геометрической модели определить, на каких промежутках оси х ординаты графика положительны (отрицательны); включить эти промежутки в ответ.
Хорошо! Теперь по цепочке, каждый из вас будет проговаривать этот алгоритм по шагам!
Отработка новых знаний.
Давайте посмотрим, насколько хорошо вы усвоили данный алгоритм.
На доске вы видите 4 графика и 5 неравенств.
Перерисуйте аккуратно графики к себе в тетрадь и установите соответствие между графиками данных функций и функциями, входящими в данное неравенство. Укажите решение.
(Учащиеся выходят к доске и сначала сопоставляют графики и вид неравенств, затем отмечают на графиках решение данных неравенств).
Молодцы! Теперь кто-нибудь из вас выйдет к доске и решит неравенство  , записывая каждый шаг алгоритма.
, записывая каждый шаг алгоритма.
(Учащиеся выходят к доске. Обращают внимание на то, что квадратное неравенство является неполным. Разбирают с учителем как решить эту проблемы. Затем, следуя алгоритму, расписывают свои действия по шагам).
Подведение итогов.
На сегодняшнем уроке мы с вами разобрали алгоритм решения квадратного неравенства с помощью графика квадратичной функции и применили его на практике.
Постановка домашнего задания.
§34, стр.200-204.
№ 34.10,№ 34.12, № 34. 23.
Урок 10: «Метод интервалов»
Предмет, класс, количество часов: Алгебра, 8 класс, 1 час.
Тип урока: урок изучения нового.
Цели:
ОЦ: Обеспечить усвоение решения квадратных неравенств методом интервалов.
ВЦ: Формирование у учащихся навыков самостоятельной работы, воспитание сообразительности, воспитание аккуратности.
РЦ: Развитие умений анализировать, выделять главное, обобщать, конкретизировать и делать выводы.
Методы обучения: объяснительно-иллюстративный, частично-поисковый, репродуктивный.
План урока
Оргмомент.
Актуализация знаний.
Введение метода интервалов при решении квадратных неравенств.
Отработка новых знаний.
Подведение итогов.
Постановка домашнего задания.
ХОД УРОКА
Оргмомент.
На прошлом занятии мы с вами познакомились с алгоритмом решения квадратного неравенства с помощью графика квадратичной функции. Сегодня мы узнаем метод, которым также часто применяется при решении неравенств. Этот метод называется методом интервалов.
Актуализация знаний.
Ребята, давайте вспомним, что мы называем корнем квадратного уравнения?
(Корнем квадратного уравнения называют всякое значение переменной х, при котором квадратный трехчлен ах2 + bx + c = 0 обращается в нуль).
Хорошо, а что значит решить квадратное уравнение?
(Значит найти все его корни или установить, что их нет).
Правильно. Ребята, а что мы понимаем под интервалом?
(Интервалом называется множество чисел или точек на прямой, заключающихся между двумя данными числами или точками a и b).
Введение метода интервалов при решении квадратных неравенств.
Давайте решим следующую задачу: Выяснить, при каких значениях x, квадратный трехчлен  принимает положительные значения, а при каких – отрицательные.
принимает положительные значения, а при каких – отрицательные.
Для начала найдем корни уравнения  .
.
Корнями являются числа  ,
,  . Поэтому можно записать .
. Поэтому можно записать .
Точки 
 разбивают числовую ось на три промежутка:
разбивают числовую ось на три промежутка:  ,
,  и
и  :
:

Двигаясь вдоль числовой оси справа налево, видим, что на интервале  трехчлен принимает положительные значения, так как в этом случае оба множителя
трехчлен принимает положительные значения, так как в этом случае оба множителя  и
и  положительны.
положительны.
На следующем интервале  этот трехчлен принимает отрицательные значения и на интервале
этот трехчлен принимает отрицательные значения и на интервале  снова положительные значения:
снова положительные значения:

Из рисунка видим, что  при
при  и
и  , а
, а  при
при  .
.
Рассмотренный способ называется методом интервалов решения квадратного неравенства.
Давайте теперь вместе попробуем сформулировать алгоритм решения квадратного неравенства методом интервалов!
(Учащиеся пытаются формулировать алгоритм, опираясь на рассмотренный пример. Учитель поправляет их:
1) Найти корни квадратного трехчлена;
2) Отметить данные корни на числовой оси;
3) Определить знак квадратного трехчлена на каждом из полученных интервалов;
4) Выбрать требуемые промежутки и записать ответ).
Отработка новых знаний.
Давайте теперь посмотрим насколько хорошо вы усвоили метод интервалов.
Немного поработаем у доски.
Задание: Решить методом интервалов неравенства:
; ;
; .
(Ученики работают у доски, проговаривая каждый шаг алгоритма вслух).
Молодцы! Теперь поработайте самостоятельно! На доске вы видите два неравенства, которые требуется решить в тетрадке методом интервалов. Будьте аккуратны при выполнении задания!
.
(Учащиеся выполняют задание самостоятельно в тетрадках. Затем учитель записывает решение на доске, и ученики сверяются с верным решением).
Подведение итогов.
На сегодняшнем уроке мы познакомились с вами с новым методом решения квадратных неравенств – методом интервалов. Вместе с вами составили алгоритм решения квадратных неравенств методом интервалов и применили его на практике.
Постановка домашнего задания.
§34, стр.205. №34.5- 34.7.
Заключение
Целью данной работы было реализовать требований ФГОС ООО при обучении учащихся 8 класса по теме: «Квадратные уравнения»
Проект состоит из двух глав и приложения.
В первой главе мной выявлены теоретические основы обучения теме, связанные с реализацией ФГОС ООО. Я рассмотрела логико-математический анализ содержания темы. Анализ понятийного аппарата показал, что в теме имеется только одно понятие, определенное явно. Анализ утверждений темы показал, что все утверждения имеют сложную форму, и все они рассмотрены с доказательствами. Анализ задачники показал, что большинство задач являются стандартными, но так же имеются задачи и для более глубокого понимания темы.
Вторая глава содержит описание методики обучения учащихся теме «Квадратные неравенства». Выполнен отбор средств обучения теме, в том числе средства ИКТ. Разработана таблица целей и карта обучения теме. Составлен фрагмент учебной рабочей программы «Тематическое и почасовое планирование образовательных результатов освоения математики по теме «Квадратные неравенства». Разработаны методические рекомендации обучения теме и применение их в учебном процессе. Разработаны фрагменты уроков, подобраны цифровые ресурсы. Выполнены все поставленные задачи и они позволили реализовать требования нового стандарта ФГОС ООО.
Список литературы
Алгебра: Учеб. Для 7 кл. / Алимов Ш.А., Ю.М. Колягин, Ю.В. Сидоров и др – М: Просвещение, 1999.
Алгебра: Учеб. Для 7 кл. общеобразовательных учреждений / Под редакцией С.А. Теляковского – М: Просвещение, 2002.
Алгебра: Учеб. Для 8 кл. / Алимов Ш.А. ., Ю.М. Колягин, Ю.В.Сидоров и др – М: Просвещение, 1991.
Алгебра: Учеб. Для 8 кл. общеобразовательных учреждений / Под редакцией С.А. Теляковского – М: Просвещение, 1996.
Алгебра: Учеб. Для 9 кл. / Алимов Ш.А. ., Ю.М. Колягин, Ю.В.Сидоров и др – М: Просвещение, 1992.
4. Алгебра.8 класс./Под ред. Виленкина Н.Я.- М: Просвещение, 1997.
5.Алгебра.9 класс./Под ред. Теляковского С.А.- М: Просвещение, 1994.
6.Алгебра в 8 кл: Методическое пособие для учителей – М: Просвещение, 1977.
7.Алгебра в 9 кл: Методическое пособие для учителей – М: Просвещение, 1978.
10. Бочарова О. Урок применения свойств линейных неравенств с одной переменной. // Математика в школе – 2002 - №7 – с. 40 – 42.
11. Виленкин Н.Я., Жохов В.И., Чесноков А.И. Математика: Учебник для 5 класса.- М: Мнемозина, 1999.
12. Галицкий М.Л., Гольдман А.Н., Завич Л.И. Курс алгебры 8-го класса в задачах- Львов: Журнал «Квантор», 1991.
13. Горбачёв В.И. Общие методы решения уравнения и неравенства с параметрами не выше 2 степени. // Математика в школе – 2000 - №2 – с. 61-68.
14. Башмаков М.И. Уравнения и неравенства – М: Наука, 1971.
15. Богушевский К.С., Сикорский К.Л. Сборник задач по математике для повторения.: Пособие для учителей 5-8 классов средней школы –М: Учпедгиз, 1955.
16. Варпаховский К.М. Элементы теории алгоритмов.- М., 1997.
17. Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами. – Киев
18. Ефремов Д.Н. Алгоритмы.- С.-Петербург, 1993.
19. Задачи по математике: Уравнения и неравенства: Справочное пособие. /Вавилов В.В. –М: Наука, 1988.
20. Здоровенко М.Ю.
21. Косовский М.А. Основы теории элементарных алгоритмов. - М.: 1987.
22. Королева Т. Математический тренажёр по алгебре для 7- 9 классов. // Математика в школе – 2001 - №8 – с.12-30.
23. Кузнецова Л. Методические указания к теме “Неравенства ” // Математика в школе – 2002 - №6 – с.22-32.
24. Кривоногов В. Квадратные неравенства и уравнения. //Математика – 2002 - №3 (16-22 января) – с.15-19.
25. Лабораторные и практические работы по методике преподавания математики. /Под ред. Лященко Е.И. - М: Просвещение,1988.
26. Ланда Л.Н. Алгоритмизация в обучении.- М.: Просвещение, 1966.
27. Математика. Арифметика. Алгебра. Анализ данных 8 кл: учебник для общеобразовательных учебных заведений. / Под редакцией Г.В. Дорофеева – М: Дрофа, 1998.
28. Математика. Арифметика. Алгебра. Анализ данных 9 кл: Учебник для общеобразовательных учебных заведений. / Под редакцией Г.В. Дорофеева – М: Дрофа, 1998.
29. Математика: Учебник для 5 класса/ Под ред. Дорофеева Г.В., Шарыгина И.Ф. - М.: Просвещение, 1994.
30. Методика преподавания математики в средней школе. /Под ред. Мишина В.И. – М.: Просвещение 1987. Талочкин П.Б. Неравенства и уравнения. – М.: Просвещение, 1970.
31. Мордкович А.Г. Алгебра 8 кл. : Задачник для общеобразовательных учреждений. – М.: Мнемозина , 2001.
32. Мордкович А.Г. и др. Алгебра 8 кл: Учебник для общеобразовательных учреждений – М: Мнемозина, 2002.
33. Мордкович А.Г. и др. Алгебра 9 кл: Задачник для общеобразовательных учреждений – М: Мнемозина, 2000.
34. Мордкович А.Г. и др. Алгебра 9 кл: Учебник для общеобразовательных учреждений – М: Мнемозина, 2000.
35.Мордкович А.Г. Алгебра: Методическое пособие для учителей.- М: Мнемозина, 1997.
36. Невяжский Г.Л. Неравенства. : Методическое пособие для учителей. – М., 1997.
37. Психология. / Под ред. Ковалёва Л.И., Степанова М.П., Шабалина Г.Т.,
Талочкин П.Б. Неравенства и уравнения. – М.: Просвещение, 1970
38. Симонов А. Дидактические материалы для 8-9 классов с углублённым изучением математики. // Математика в школе – 2002 - №7 – с.5-10.
39. Факультативный курс по математике: Учебное пособие для 7-9 классов средней щколы /сост. Никольская И.Л. – М.: Просвещение, 1991.
Приложение
Факультативное занятие в 8 классе (решение неравенств с параметром первой степени с одной неизвестной).
Цель:
применить алгоритмический метод при формировании умений и навыков в решении линейных неравенствах с параметрами.
Задачи:
расширить кругозор учащихся;
воспитание внимания, аккуратности, самостоятельности;
осуществление взаимосвязи теории и практики;
развитие памяти, логического мышления.
Решение задач с параметрами всегда вызывает большие трудности у учащихся. Причём часто учащиеся испытывают психологические трудности, «боятся» таких задач, так как не видят связи в их решении с решениями линейных неравенств с одной переменной.
Изучение линейных неравенств с параметром первой степени с одной неизвестной не возможно без умения решать линейные неравенства с одной переменной. Так как факультатив проводился в 9 классе, а линейные неравенства изучались в восьмом классе, то возникла необходимость актуализировать знания по решению линейных неравенств, вспомнить этапы их решения. Ученикам можно предложить следующее задание.
Решите неравенство 2(х+5)-3≥4+3х
Все решают у себя в тетрадях, а один ученик решает у доски. Запись ведёт в два столбика. Решение в одном столбика, а в другом записывают пояснения к своим действиям.

2х+7≥4+3х Раскрыли скобки в обеих частях неравенства
2х-3х≥4-2 Перенесли слагаемые, содержащие переменную в одну
часть, а не содержащую в другую.
-х≥2 Привели подобные члены в каждой части.
х≤-2 Разделили обе части неравенства на коэффициент при

переменной (учитывая его знак !).
Отметили соответствующие промежутки на
координатной прямой.
х (-∞;-2] Записали числовой промежуток
(-∞;-2] Записали числовой промежуток
После того как повторили этапы решения линейных неравенств с одной переменной, учитель предлагает на доске подробный разбор решения неравенства с параметром. Затем ученики вместе с учителем формулируют алгоритм решения линейных неравенств с параметром.
Пример 1. Рассмотрим решение неравенства (а-4)∙х
Чтобы найти х, обе части неравенства хочется разделить на (а-4). Однако теперь важно положительно, отрицательно или равно нулю выражение (а-4).
Определим знак выражения





(а-4)
а
4
Рассмотрим три случая:
а-4=0
а-40
а-40
1)если а-4=0 а=4, то неравенство примет вид 0хR
а=4, то неравенство примет вид 0хR
2) a-40  a4, то разделим обе части неравенства на положительное выражение (а-4), не меняя знак неравенства, получим х
a4, то разделим обе части неравенства на положительное выражение (а-4), не меняя знак неравенства, получим х  (используем свойство числового неравенства).
(используем свойство числового неравенства).
3) a-4a.
Ответ:
если а=4, то х  R;
R;
если а4, то х  ;
;
если а.
Таким образом, после разобранного примера учитель формулирует алгоритм, опираясь на знания и умения, учащихся о решении линейных неравенств с одной переменной.
Раскрыть скобки в обеих частях неравенства (если есть дробные коэффициенты, то неравенство освободить от дробей).
Перенести слагаемые, содержащие переменную в одну часть, а не содержащие в другую.
3. Привести подобные члены в каждой части и получить один из 4 видов неравенств А(а)хB(a) (**) , А(а)х≤B(a), А(а)хB(a), А(а)х≥B(a), где х- переменная, А(а) и В(а) – функции параметра а.
4. Рассмотреть три случая:
1) Найти а, при которых А(а)=0, подставить в неравенство(**) вместо параметра а найденные решения и решить соответствующие неравенства.
2) Найти а, при которых А(а)0, разделить неравенство(**) на А(а), не меняя его знак.
3) Найти а, при которых А(а)
5. Записать ответ.
Пример 2. решить неравенство





3-а∙х ≥ х  х+а∙х≤3
х+а∙х≤3  х∙(1+а)≤3
х∙(1+а)≤3
-1
1+а=0 а=-1
а=-1
Подставляем в неравенство 0∙х≤3, х R.
R.
1+а0 а-1
а-1
х≤
1+аа
x≥
Ответ: При а=-1, то х R;
R;
а-1, то х ≤  ;
;
аx ≥  .
.
Пример 3.
х∙а2 ≤ а+х х∙ (а2-1) ≤ а
х∙ (а2-1) ≤ а





1) а2-1=0 (а-1)(а+1)=0
(а-1)(а+1)=0 а=1 или а=-1
а=1 или а=-1

а = 1; а = -1; х∙0 ≤ 1 неверно
1
-1
Ответ: а=1, то х R;
R;
а= -1, то нет решения;
 , то x ≤
, то x ≤ ;
;
 , то x
, то x 
 .
.
Пример 4.
2а∙(а-2) ∙х  а-2
а-2
1) 2а∙(а-2)=0 а=0 или а=2
а=0 или а=2
а=0 х∙0 -2 верно
-2 верно




а=2 х∙0 0 неверно
0 неверно
2) 2а∙(а-2)0 а
а ,
,
то х

3) 2а∙(а-2)  , то х
, то х

Ответ:
а=0, то х R;
R;
а=2, то нет решения;
а , то х
, то х
 ;
;
 , то х
, то х
 .
.
Пример 5.
(а2-9) ∙х а+3
а+3



1) а2-9=0 
а=3 и а=-3
а=3 0х 6 верно;
6 верно;
а=-3 0х 0 верно;
0 верно;
2) 
 ;
;
3) 
 ;
;
Ответ:
а=3 , а=-3 то х R;
R;
 , то
, то ;
;
 , то
, то  ;
;
Пример 6.
а2х-а ∙х a-1 x∙ (a2-a) a-1
x∙ (a2-a) a-1 x∙(a∙ [a-1]) a-1
x∙(a∙ [a-1]) a-1
a∙ [a-1]=0 a=0 и а=1
a=0 и а=1


а=0 0∙х-1 верно
а=1 0∙х0 неверно
2) ; х
; х
3)а ; х
; х
Ответ:
а=0, то х R;
R;
а=1, то нет решения;
a , то х
, то х ;
;
 , то х.
, то х.
Пример 7.
а2∙х+4а∙х-а-4≤0
Ответ:
а=0 , а=-4 то х R;
R;
 , то
, то ;
;
 , то
, то  .
.
Пример 8.

Ответ:
a
а , то х ;
, то х ;
 , то х
, то х .
.
Примеры для самостоятельного решения:
1)2∙а∙х+5а+10∙x;
2)a∙x+x+1
3)x+1≤a∙x+a2;
4)a∙x+16≤a2-4∙x;
5)m∙x1+3∙x;
6) ;
;
7) ;
;
8) (x-1) ∙ (a2-1)5-4∙a;
9)b-3∙b+4∙b∙xb+12∙x;
Интернет-ресурсы:
www.edu.ru
www.school.edu.ru
www.math.ru
www.etudes.ru

 Получите свидетельство
Получите свидетельство Вход
Вход






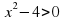 ;
; 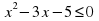 ;
; 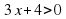 ;
; 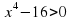 ;
;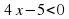 .
.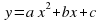 совпадает со знаком числа а.
совпадает со знаком числа а.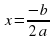 , знак квадратичной функции
, знак квадратичной функции 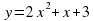 ;
; 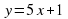 ;
; 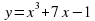 ;
; 








 Проект по математике "Реализация требований ФГОС ООО при обучении учащихся теме: «Квадратные неравенства»" (0.42 MB)
Проект по математике "Реализация требований ФГОС ООО при обучении учащихся теме: «Квадратные неравенства»" (0.42 MB)
 0
0 1440
1440 137
137 Нравится
0
Нравится
0


