Тип проекта – информационный, практико - ориентированный.
Средняя продолжительность – 2 недели (краткосрочный)
Цель проекта – создание условий для углубления и систематизации знаний по теме “Действия с многочленами ”.
Задачи проекта:
систематизировать определения и правила
систематизировать задачи по данной теме
отработать навыки решения нестандартных задач
изготовить продукт для кабинета математики, который можно использовать на уроках.
В классе выделена группа из трех человек, которая работает в автономном режиме. В течение первой недели ребята подбирали интересные, необычные задачи, в которых используются действия над многочленами. Во время урока они обсуждают решения этих задач, получают необходимые консультации. В качестве домашнего задания – оформление решенных задач и поиски новых.
Задачи были систематизированы следующим образом:
Действия с числами вида SHAPE * MERGEFORMAT .
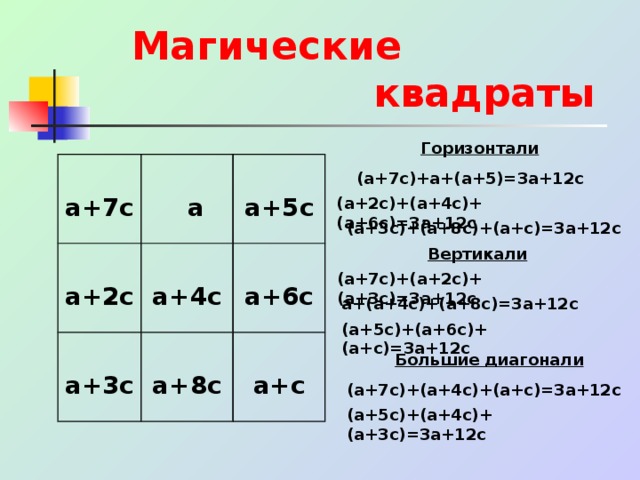
Магические квадраты.
Задачи на доказательство кратности выражения.
Задачи, решаемые с помощью уравнений.
Задачи с использованием формул.
Задачи олимпиадного характера.

На заключительном этапе работы:
1) проведена защита проекта;
2) выполнен самоанализ работы группы и анализ результатов работы учащимися класса.

 Получите свидетельство
Получите свидетельство Вход
Вход




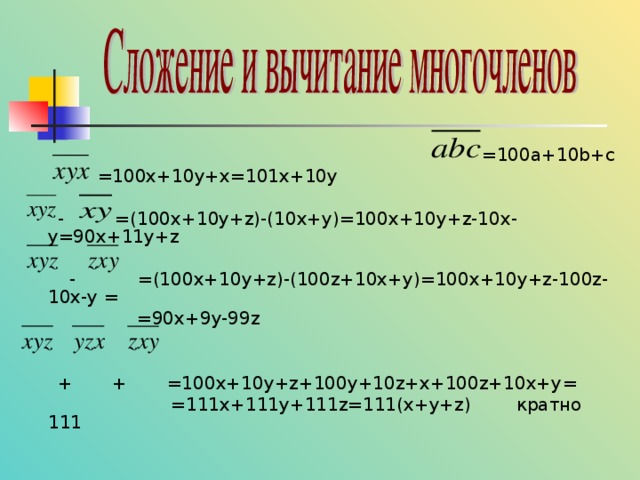

 x ( x +2) на 13 ( x +1)( x +3)= x ( x +2)+13 x ² +3 x + x +3= x ² +2 x +13 x ² - x ² +3 x + x -2 x =13-3 2 x =10 x =10:2 x =5 Значит, I число равно 5. II число: 5+1=6, III число: 5+2=7, IV число:5+3=8 Ответ : 5, 6, 7, 8. " width="640"
x ( x +2) на 13 ( x +1)( x +3)= x ( x +2)+13 x ² +3 x + x +3= x ² +2 x +13 x ² - x ² +3 x + x -2 x =13-3 2 x =10 x =10:2 x =5 Значит, I число равно 5. II число: 5+1=6, III число: 5+2=7, IV число:5+3=8 Ответ : 5, 6, 7, 8. " width="640"












 Проект по математике "Действия с многочленами в нестандартных задачах" (0.14 MB)
Проект по математике "Действия с многочленами в нестандартных задачах" (0.14 MB)
 0
0 1734
1734 92
92 Нравится
0
Нравится
0


