Примеры решений заданий ЕГЭ профильного уровня по теме «Первообразная и интеграл»
Тема «Первообразная и интеграл» включена в кодификатор элементов содержания по математике для составления КИМов для проведения
Единого государственного экзамена профильного уровня. Анализ спецификации и материалов открытого банка заданий ЕГЭ показал, что применение первообразной встречается в заданиях под номером 6. Можно выделить следующий тип задач на применение первообразной в заданиях ЕГЭ профильного уровня: применение геометрического смысла первообразной (вычисление площади плоской фигуры);
Пример 1
На рисунке изображён график некоторой функции 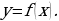 Функция
Функция 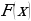
— одна из первообразных функции 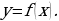 Найдите площадь закрашенной фигуры.
Найдите площадь закрашенной фигуры.
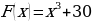
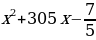



Рисунок 1
Решение:
Решая данную задачу или аналогичные задачи, учащимся необходимо ответить на следующие вопросы:
Какая фигура изображена на рисунке?
Как или с помощью какой формулой можно найти площадь этой фигуры?
Как с помощью данной формулы найти площадь фигуры и при этом, по возможности, упростить вычисления?
Фигура, изображенная на рисунке, ограничена сверху графиком функции 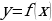 , снизу осью Ох, а по бокам прямыми у =
, снизу осью Ох, а по бокам прямыми у = 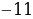 и у =
и у = 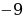 . Следовательно данная фигура является криволинейной трапецией.
. Следовательно данная фигура является криволинейной трапецией.
Отвечая на 1 вопрос, у учащихся могут возникнуть затруднения в определении вида фигуры. На рисунке 12 приведем примеры прямолинейных трапеции различного вида.
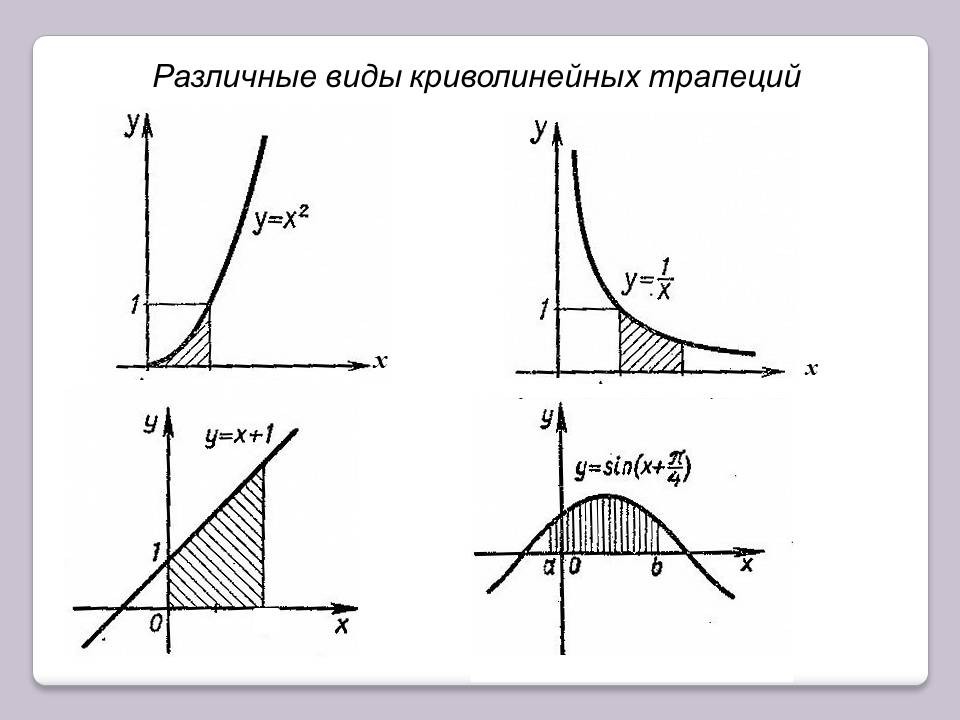
Рисунок 2– Различные виды криволинейной трапеции
Выяснив, что данная фигура представляет собой криволинейную трапецию, вспомним, по какой формуле можно найти площадь криволинейной трапеции. Это формула Ньютона — Лейбница.
S = 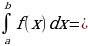 F(b) – F(а), где F(a) и F(b) –первообразные функции
F(b) – F(а), где F(a) и F(b) –первообразные функции 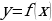 в точках а и b.
в точках а и b.
Решая данную задачу, обычно учащиеся отдельно находят 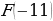 и
и 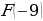 .
.
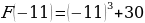
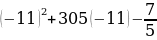 =
=
=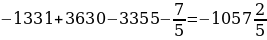
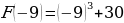

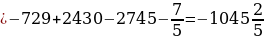
Потом, по формуле Ньютона – Лейбница, находят разность

При таком решении возникает вероятность появления арифметических ошибок, а именно возведение в четную и нечетную степень отрицательных чисел, умножение, сложение и вычитание целых и дробных чисел. Для уменьшения этой вероятности я предлагаю следующую форму записи вычислений.
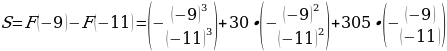
Данная схема позволяет не учитывать свободные члены, так как их разность равна 0. Далее определяем знаки в каждых скобках. Учитываем, что функция 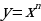 при n
при n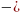 четное число, является четной, а при n
четное число, является четной, а при n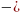 нечетное число является нечетной. Если степень нечетная, то скобках меняем знак «
нечетное число является нечетной. Если степень нечетная, то скобках меняем знак «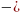 » на знак «+» и меняем местами уменьшаемое и вычитаемое, есть ли степени четное то в скобках меняем знак «
» на знак «+» и меняем местами уменьшаемое и вычитаемое, есть ли степени четное то в скобках меняем знак «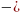 » на знак «+» и разность оставляем без изменений.
» на знак «+» и разность оставляем без изменений.
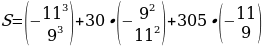
Далее возводим степень и вычитаем столбик.
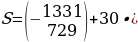
Производим вычисления, по возможности сокращая и учитывая знак произведения.
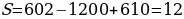
Ответ:12
Пример 2
На рисунке изображен график некоторой функции y = f (x). Функция F(x) — одна из первообразных функции f (x). Найдите площадь закрашенной фигуры. В ответе запишите площадь, умноженную на 3.
![]()
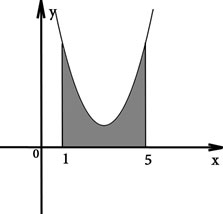
Рисунок 3
Решение:
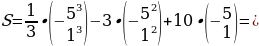
 =
=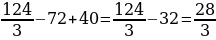
В ответе записываем площадь, умноженную на 3:

Ответ: 28
Пример 3.
На рисунке изображен график некоторой функции y = f (x). Функция F(x) — одна из первообразных функции f (x). Найдите площадь закрашенной фигуры. В ответе запишите площадь, умноженную на 3.
![]()
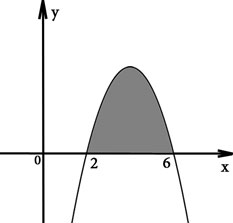
Рисунок 4
Решение:
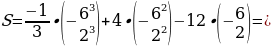
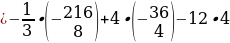 =
=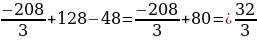
В ответе записываем площадь, умноженную на 3:
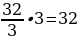
Ответ: 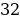
Пример 4
На рисунке изображен график функции f (x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F (7) − F (0), где F (x) — одна из первообразных функции f (x).
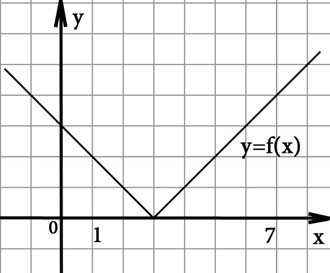
Рисунок 5
Решение:
Выражение F (7) − F (0) является частью формулы Ньютона — Лейбница:
S = 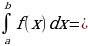 F(b) – F(а),
F(b) – F(а),
где F(a) и F(b) – первообразные функции 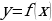 в точках а и b.
в точках а и b.
В нашем случае а = 0 и b = 7. Следовательно значение выражения
F (7) − F (0) равно площади криволинейной трапеции ограниченной графиком функции f (x), осью иксов и прямыми x = 7 и x = 0. В данном случае криволинейная трапеция представляет собой два прямоугольных треугольника. Площадь прямоугольного треугольника находим как половина произведения катетов.
F (7) − F (0) =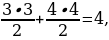 5+8=12,5
5+8=12,5
Ответ: 12,5
Пример 5
На рисунке изображен график некоторой функции 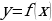 Пользуясь рисунком, вычислите определенный интеграл
Пользуясь рисунком, вычислите определенный интеграл 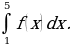
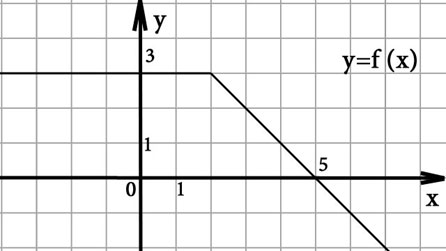
Рисунок 6
Решение:
По формуле Ньютона — Лейбница:
S = 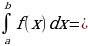 F(b) – F(а),
F(b) – F(а),
где F(a) и F(b) – первообразные функции 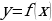 в точках а и b.
в точках а и b.
В нашем случае а = 1 и b = 5. Следовательно значение интеграла 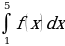
равно площади криволинейной трапеции ограниченной графиком функции f (x), осью иксов и прямыми x = 5 и x = 1. В данном случае криволинейная трапеция представляет собой трапецию с основаниями, равными 1 и 4 и высотой, равной 3.
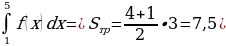
Так же площадь трапеции можно найти как сумму площади прямоугольника со сторонами 1 и 3 и равнобедренного прямоугольного треугольника с катетами, равными 3 (так как любой многогранник можно разделить на конечное число прямоугольников и прямоугольных треугольников).
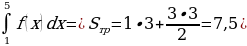
Ответ: 7,5

 Получите свидетельство
Получите свидетельство Вход
Вход












 Примеры решений заданий ЕГЭ профильного уровня по теме «Первообразная и интеграл» (144.79 KB)
Примеры решений заданий ЕГЭ профильного уровня по теме «Первообразная и интеграл» (144.79 KB)
 0
0 146
146 4
4 Нравится
0
Нравится
0


