Примерная экзаменационная работа по математике для студентов СПО
Критерии оценки итоговой работы:
| Оценка
| Число баллов, необходимое для получения оценки |
| «3» (удовлетворительно) | 9–14
|
| «4» (хорошо) | 15–20 (не менее одного задания из дополнительной части)
|
| «5» (отлично) | 21–30 (не менее двух заданий из дополнительной части)
|
1Вариант
Обязательная часть
При выполнении заданий 1-8 запишите ход решения и полученный ответ.
(1 балл) В сентябре 1 кг винограда стоил 80 рублей. В октябре подорожал на 15% , а в ноябре еще на 20%. Сколько рублей стоил 1кг винограда после подорожания в ноябре.
(1 балл) Вычислите площадь фигуры (S), ограниченной линиями y=x³+1, Y=0, x=0, x=2
(1 балл) определите, какие из перечисленных точек принадлежат графику функции y(x)=4x-3. А(1;-5); В(0;-3); С(2;5); D (-1,6).
(1 балл) Вычислите значение выражения (2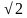 -4)(2
-4)(2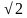 +4).
+4).
(1 балл) Найдите значение cosα, если sinα= -0,8, π˂α˂ 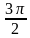 .
.
(1 балл) Решите уравнение:76-х=49х
(1 балл) Вычислите значение выражения log38-2log32+log3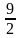 .
.
(1 балл) Решите уравнение: lg(3-x)-lg(x+2)=2lg2.
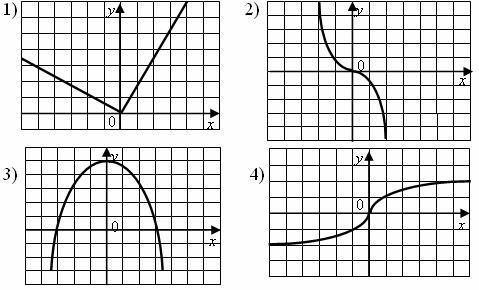
(1 балл) Определите, какой из приведенных графиков соответствует четной функции и кратко поясните, почему.
Используя график функции y=f(x) (см. рис. ниже), определите и запишите ответ:
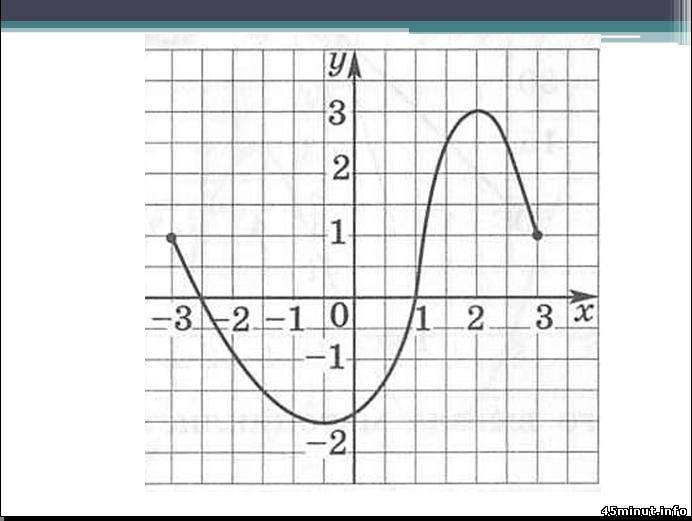
(1балл) наименьшее и наибольшее значение функции;
(1балл) промежутки возрастания и убывания функции;
1(балл) при каких значениях x f(x)≥0.
При выполнении задания 13-18 запишите ход решения и полученный ответ
(1 балл) Из точки B к плоскости α проведены две наклонные длиной 10 и 17 см.
Расстояние от точки B до плоскости α равно 8 см. Найдите проекции наклонных.
(1 балл) Найдите значение производной функции: y= - 4x²+3x-1 в точке x0=2.
(1балл) Найдите область определения функции y=log0.5(x²-4x)
(1 балл) Решите уравнение: 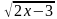 -
- 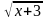 =0
=0
(1 балл) Решите уравнение: 2cos² x-3sin x cos x+sin²x=0
(1 балл) Высота правильной четырехугольной пирамиды равна 12 см, а сторона основания 18см. Найдите площадь боковой поверхности пирамиды.
Дополнительная часть
При выполнении заданий 19-22 запишите ход решения и полученный ответ
(3 балла) Найдите экстремумы функции y=x³+3x²-9x
(3 балла) Решите неравенство 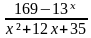 ≥0
≥0
(3балла) Площадь осевого сечения цилиндра равна 64см², а его образующая равна диаметру основания. Найдите объем цилиндра.
(3 балла) Решите систему уравнений:
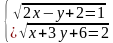
2Вариант
Обязательная часть
При выполнении заданий 1-8 запишите ход решения и полученный ответ.
(1 балл) В сентябре 1 кг клубники стоил 120 рублей. В октябре подорожала на 25% , а в ноябре еще на 30%. Сколько рублей стоил 1кг клубники после подорожания в ноябре.
(1 балл) Вычислите площадь фигуры (S), ограниченной линиями y=4-x², Y=0, x= -2, x=2
(1 балл) Определите, какие из перечисленных точек принадлежат графику функции y(x)=-2 x+5. А(-1;7); В(3;0); С(1;3); D (0,4).
(1 балл) Вычислите значение выражения (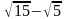 ) (
) (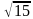 +
+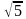 ) .
) .
(1 балл) Найдите значение sinα, если cosα= 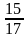 ,
, 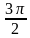 ˂α˂2π.
˂α˂2π.
(1 балл) Решите уравнение: 6²х-6 · 65-3x =216
(1 балл) Вычислите значение выражения: log522-log511-log510
(1 балл) Решите уравнение: lg(3x-2)=3-lg25.
(1 балл) Определите, какой из приведенных графиков соответствует нечетной функции и кратко поясните, почему.
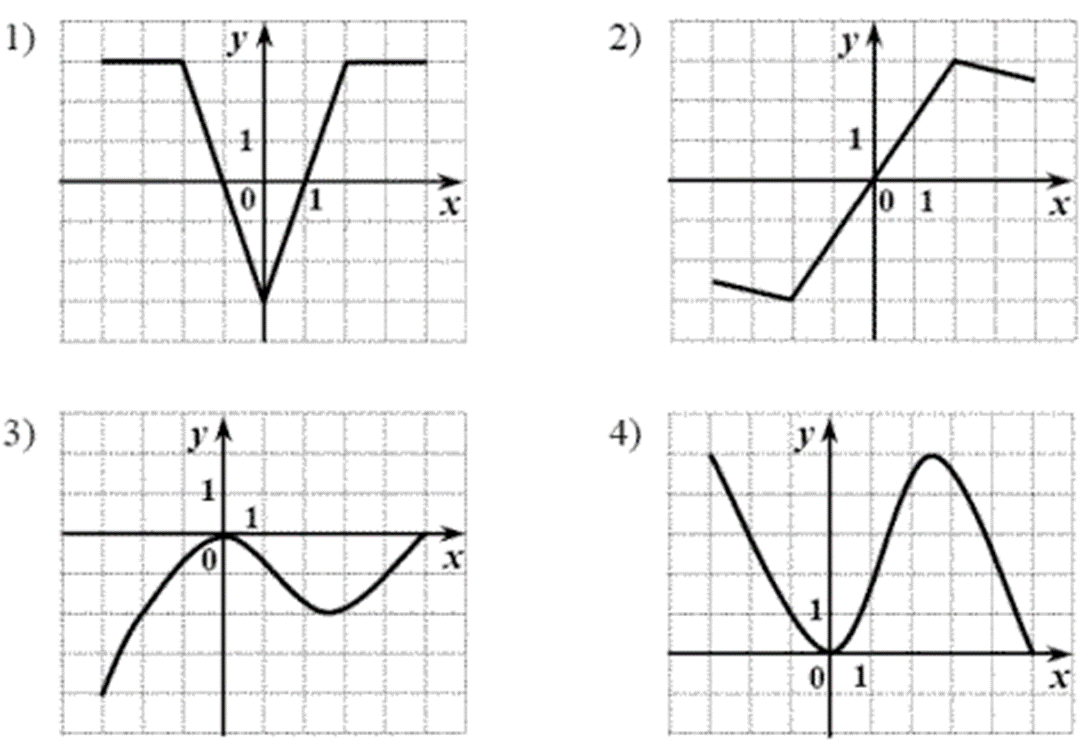
Используя график функции y=f(x) (см. рис. ниже), определите и запишите ответ:
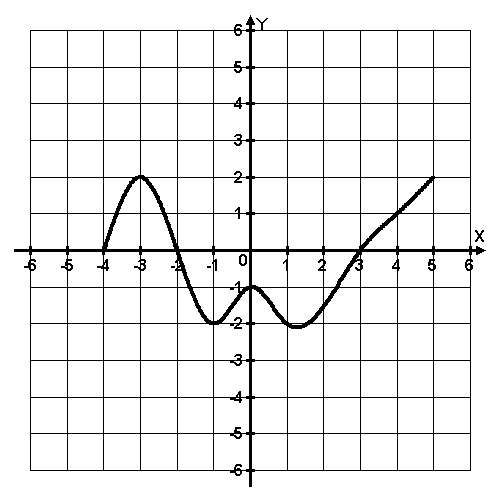
(1балл) наименьшее и наибольшее значение функции;
(1балл) промежутки возрастания и убывания функции;
1(балл) при каких значениях x f(x)≤0.
При выполнении задания 13-18 запишите ход решения и полученный ответ
(1 балл) Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если одна из них на 26м больше другой, а проекции наклонных равны 12м и 40 м.
(1 балл) Найдите значение производной функции: y= 7x²-56x+8 в точке x0=4.
(1балл) Найдите область определения функции y=log3(2ˣ-1).
(1 балл) Решите уравнение: x -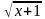 =1
=1
(1 балл) Решите уравнение: cos² x+3 cos x=0
(1 балл) Основанием пирамиды служит прямоугольник со сторонами 6 м и 15 м. Высота пирамиды, равная 4 м, проходит через точку пересечения диагоналей основания . Найдите площадь боковой поверхности пирамиды.
Дополнительная часть
При выполнении заданий 19-22 запишите ход решения и полученный ответ
(3 балла) Найдите экстремумы функции y=- x³+9x²+21x
(3 балла) Решите неравенство 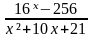 ≤0
≤0
(3балла) Осевое сечение конуса- равносторонний треугольник. Площадь боковой поверхности этого конуса равна 5 см². Найти площадь полной поверхности конуса.
(3 балла) Решите систему уравнений:
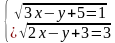
3Вариант
Обязательная часть
При выполнении заданий 1-8 запишите ход решения и полученный ответ.
(1 балл) Держатели дисконтной карты книжного магазина получают при покупке скидку 6%.Книга стоит 650 руб. Сколько руб. заплатит держатель дисконтной карты за эту книгу?
(1 балл) Вычислите площадь фигуры (S), ограниченной линиями y=1-x³, Y=0, x= 0, x=1
(1 балл) Определите, какие из перечисленных точек принадлежат графику функции y(x)=7x-1, А(2;7); В(-1;3); С(0;-1); D (1,6).
(1 балл) Вычислите значение выражения ( ) (
) (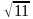 +
+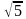 ) .
) .
(1 балл) Найдите значение cosα, если sinα= 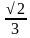 , 0˂α˂
, 0˂α˂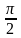 .
.
(1 балл) Решите уравнение: 5²х-6 =
(1 балл) Вычислите значение выражения log45+log425+log4
(1 балл) Решите уравнение: lоg2(4-x)+log2(1-2x)=2log23.
(1 балл) Определите, какие из приведенных графиков соответствуют четной функции и кратко поясните, почему.
Используя график функции y=f(x) (см. рис. ниже), определите и запишите ответ:
(1балл) наименьшее и наибольшее значение функции;
(1балл) промежутки возрастания и убывания функции;
1(балл) при каких значениях x f(x)≥0.
При выполнении задания 13-18 запишите ход решения и полученный ответ
(1 балл) Из точки к плоскости проведены две наклонные, равные 23см и 33см . Найдите расстояние от этой точки до плоскости, если проекции наклонных относятся как 2:3 .
(1 балл) Найдите значение производной функции: y= x - 4 в точке x0=4.
(1балл) Найдите область определения функции y=lg(1-3ˣ).
(1 балл) Решите уравнение: (x²-9) =0
(1 балл) Решите уравнение: 3sin²x+sinx cosx=2cos²x
(1 балл) В правильной четырех угольной пирамиде высота равна 3м , боковое ребро 5м. Найти объем пирамиды.
Дополнительная часть
При выполнении заданий 19-22 запишите ход решения и полученный ответ
(3 балла) Найдите экстремумы функции y=5+12 x-х³
(3 балла) Решите неравенство ˃0
(3балла) Радиус основания цилиндра равен 6см, высота в два раза меньше длины окружности основания. Найдите площадь полной поверхности цилиндра.
(3 балла) Решите уравнение:
-
=0
4Вариант
Обязательная часть
При выполнении заданий 1-8 запишите ход решения и полученный ответ.
(1 балл) Держатели дисконтной карты книжного магазина получают при покупке скидку 7%.Книга стоит 200руб. Сколько руб. заплатит держатель дисконтной карты за эту книгу?
(1 балл) Вычислите площадь фигуры (S), ограниченной линиями y=х² - 4x+5, Y=0, x= 0, x=4
(1 балл) Определите, какие из перечисленных точек принадлежат графику функции y(x)= - 6x+5, А(0;5); В(-1;-1); С(2;-5); D (-1,11).
(1 балл) Вычислите значение выражения ( ) (
-4) .
(1 балл) Найдите значение sinα, если cosα= - ,
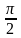 ˂α˂π.
˂α˂π.
(1 балл) Решите уравнение: ( )x-8 =8.
(1 балл) Вычислите значение выражения 2log732-log7256-2log714
(1 балл) Решите уравнение: lоg5(x-10)=2+log52.
(1 балл) Определите, какие из приведенных графиков соответствуют нечетной функции и кратко поясните, почему.
Используя график функции y=f(x) (см. рис. ниже), определите и запишите ответ:
(1балл) наименьшее и наибольшее значение функции;
(1балл) промежутки возрастания и убывания функции;
1(балл) при каких значениях x f(x)≤0.
При выполнении задания 13-18 запишите ход решения и полученный ответ
(1 балл) Из точки к плоскости проведены две наклонные, которые относятся как 1 : 2 . Найдите длины наклонных, если проекции наклонных равны 1 см и 7 см .
(1 балл) Найдите значение производной функции: y= x - в точке x0=
.
(1балл) Найдите область определения функции y=lg(1-5ˣ).
(1 балл) Решите уравнение: (x²-4) =0
(1 балл) Решите уравнение: 9sinxcosx-7cos²x=2sin²x
(1 балл) В прямой треугольной призме стороны основания равны 3см, 4см и 5см ,а высота равна 6 см. Найдите её полную поверхность.
Дополнительная часть
При выполнении заданий 19-22 запишите ход решения и полученный ответ
(3 балла) Найдите экстремумы функции y=9+8х²-x4
(3 балла) Решите неравенство ≤0
(3балла) Угол при вершине осевого сечения конуса равен 60 ,образующая его равна 2√3 м. Найдите объём конуса.
(3 балла) Решите уравнение:
-
=0

 Получите свидетельство
Получите свидетельство Вход
Вход












 Пример экзаменационной работы по математике для студентов СПО (393.39 KB)
Пример экзаменационной работы по математике для студентов СПО (393.39 KB)
 0
0 1109
1109 28
28 Нравится
0
Нравится
0


