Прикладные задачи "Объмы тел"

Геометрия, 11 класс.

Прикладные задачи

Объемы геометрических тел.

Пояснительная записка

Одним из моментов в модернизации современного математического образования является усиление прикладной направленности школьного курса математики, то есть осуществление связи его содержания и методики обучения с практикой.

Прикладная направленность обучения математике предполагает ориентацию его содержания и методов на тесную связь с жизнью, основами других наук, на подготовку школьников к использованию математических знаний в предстоящей профессиональной деятельности.

Одним из основных средств, применение которого создает хорошие условия для достижения прикладной и практической направленности обучения математике, являются задачи с практическим содержанием (задачи прикладного характера). Независимо от того, какой жизненный путь и профессию выберут выпускники в дальнейшем, опыт решения «жизненных» задач, несомненно, пригодится им в жизни и поможет адаптироваться к изменениям, происходящим в обществе.

Удачно подобранные задачи прикладного содержания способны пробудить интерес, создать уверенность в её полезности, её практической значимости, укрепить представления о возникновении и развитии математики в результате практической, производственной деятельности людей, показать значимость и ценность теоретических знаний.

Прикладные задачи целесообразно использовать в процессе обучения для достижения таких дидактических целей как:

• мотивация введения новых математических понятий и методов;

• иллюстрация учебного материала;

• закрепление и углубление знаний по предмету;

• формирование практических умений и навыков.

Решение прикладных задач по геометрии позволяет усилить практическую направленность изучения школьного курса геометрии; выработать необходимые навыки решения практических задач, умения оценивать величины и находить их приближенные значения; сформировать представления о соотношениях размеров реальных объектов и связанных с ними геометрических величин; повысить интерес, мотивацию и, как следствие, эффективность изучения геометрии.

Используя в старших классах при изучении геометрии блочную подачу учебного материала, как одно из средств интенсивного обучения математики, у меня высвободилось время для повторения вопросов теории и особенно решения задач. Понимая, что более глубокое осмысление теории происходит при решении различных задач, мне пришлось разнообразить представленные задачи в учебнике путём усиления практической и прикладной направленности их содержания.

Опыт работы показывает, что решение задач прикладного характера для одного ученика являются простым и понятным, а для другого – сложным. Поэтому данный дидактический материал можно использовать как при работе со всем классом, так и для самостоятельной и индивидуальной работы с учащимися. В своей работе я практикую использование дидактического материала следующим образом: если класс подготовленный, то задачи решают индивидуально, а если класс слабый, то задачи решают парами. При индивидуальной работе школьников я использую рейтинговую систему оценивания, т.е. чем больше учащихся класса решили данную задачу, тем меньше баллов за неё получает ученик. Для решения прикладных задач по каждой теме выделяю не менее 2 часов. Домашним заданием для учащихся (желающих) может служить творческое задание - придумать задачу с практическим содержанием, которая в дальнейшем пополнит содержание данных дидактических материалов.

Прикладные задачи

Объемы геометрических тел.

1. Египетские пирамиды – древнейшее и вместе с тем единственное сохранившееся до наших дней чудо света. Пирамида Хеопса имеет форму правильной четырехугольной пирамиды. Высота пирамиды на сегодняшний день составляет 138,75 м, сторона основания 230м. Вычислите объем пирамиды.

2. Вычислите количество нефти в тоннах, находящейся в цистерне цилиндрической формы, диаметр которой равен 22 м, а высота 8м, плотность нефти 800 кг/м³.

3. Три латунных куба с рёбрами 3см, 4см и 5см переплавлены в один куб. Какую длину имеет ребро этого куба?

4. Какой объем молока может войти в тетрапак в виде пирамиды, основание которой равносторонний треугольник со стороной 20см, высотой 24см.

5. Найти диаметр медной проволоки, если 30м проволоки весят 121,2г и плотность меди 8,9г/см³.

6. Сколько шариков диаметром в 1см можно отлить из куска свинца весом в 1 кг, если плотность свинца 11,4 г/см³?

7. Сколько литров воды вмещает водоём, имеющий форму правильной четырехугольной усеченной пирамиды, если глубина его равна 1,2 м, а стороны оснований – 10м и 5м?

8. Найдите объем детали, изображенной на рисунке (все двугранные углы – прямые).

9. Автоцистерна для перевозки молока имеет форму цилиндра. Внутренний диаметр, которого равен 1,4 м, а длина - 3,5 м. Сколько тонн молока можно налить в такую цистерну, если заполнить ее доверху? Плотность молока 1032 кг/м³.

10. В цилиндрический сосуд, в котором находится 6 дм³ воды, опустили деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали?

11. Куча щебня имеет коническую форму, радиус основания которой 2м и образующая 3,5м. Сколько надо возов, чтобы перевезти весь щебень, уложенный в десяти таких кучах, если 1 м³ щебня весит 3 т и на один воз грузят 0,5 т.

12. Прямоугольный золотой лист имеет размеры 4,7см × 6,2см и весит 6,3г. Найдите толщину листа (плотность золота 19,3г/см³).

13. Бак, имеющий форму правильной четырехугольной усеченной пирамиды, вмещает 190л бензина. Найдите глубину этого бака, если стороны его оснований равны 60см и 40см.

14. Железнодорожная насыпь дана в разрезе (см. чертёж); размеры указаны в метрах. Найти, сколько кубических метров земли приходится на 1 км насыпи.

15. Внутренний диаметр чугунного полого шара 8см, а внешний 10см. Найти вес шара (плотность чугуна 7,3г/см³).

16. Стаканчик для мороженого конической формы имеет 12см глубину и 5см по диаметру верхней части. На него сверху положили две ложки мороженного в виде полушарий диаметра 5см. Переполнит ли мороженое стаканчик если позволить ему растаять.

17. Свинцовая труба с толщиной стенок в 4 мм имеет внутренний диаметр 13 мм. Сколько весят 25 м этой трубы, если плотность свинца 11,4г/см³?

18. На полке в магазине стоят две банки цилиндрической формы земляничного варенья одного и того же сорта. Одна банка в 2 раза выше другой, но зато её диаметр в 2 раза меньше. Высокая банка стоит 23 цента, а низкая 43 цента. Какую из банок купить выгоднее?

19. Стог сена имеет форму цилиндра с коническим верхом. Радиус его основания 2,5 м, высота 4м, причём цилиндрическая часть стога имеет высоту 2,2 м. Определить вес стога (плотность сена 0,03г/см³).

20. Стальной вал, имеющий 1,40 м длины и 0,083 м в диаметре, обтачивается на токарном станке, причём его диаметр уменьшается на 0,003 м. Сколько он теряет в весе благодаря обточке? (плотность стали 7,4г/см³)

21. Жидкость, налитая в конический сосуд, имеющий 0,18 м высоты и 0,24 м в диаметре основания, переливается в цилиндрический сосуд, диаметр основания которого 0,10 м. Как высоко будет стоять уровень жидкости в сосуде?

22. Из 10 кг свинца отливают куб. Найти ребро куба. (Плотность свинца 11,4; угарный газ во внимание не принимается).

23. Медный прямоугольный параллелепипед, ребра которого равны 20 см, 20 см и 10 см, переплавлен в шар. Найдите радиус шара. (Примите .)

1. Найдите объем детали, изображенной на рисунке (все двугранные углы – прямые).

2. Бак имеет форму усеченного конуса, радиусы оснований которого равны 30см и 20см, а высота – 24см. Определите вместимость этого бака. В мензурке (цилиндрический сосуд с делениями на кубические сантиметры) расстояние между двумя смежными делениями 1,8 см. Найти внутренний диаметр мензурки.

3. Сколько досок длиной 3,5 м, шириной 20 см и толщиной 20 мм выйдет из четырехугольной балки длиной 105 дм, имеющей в сечении прямоугольник размером 30 см x 40 см?

4. Сколько нужно взять медных шаров радиуса 2 см, чтобы из них можно было выплавить шар радиуса 6 см?

5. Металлический шар радиусом 100мм надо перелить в цилиндр, высота которого равна 100мм. Найдите длину радиуса основания цилиндра.

6. Стальной конус, имеющий в диаметре 25см и высоту 30см, стачивается до 20см в диаметре, причем остается та же высота. На сколько уменьшится объём конуса?

7. Прямолинейный участок дороги шириной 10 м и длиной 100 м требуется покрыть асфальтом толщиной 5 см. Сколько потребуется машин асфальта, если объемный вес асфальта равен 2,4 т/м³, а грузоподъемность одной машины – 5 тонн?

8. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 16 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого?

9. Сколько надо назначить рабочих, чтобы большими лопатами окончить в 6 часов рытьё канавы длиной в 25м? Размеры (в метрах) указаны на чертеже. (Большой лопатой выкапывают 0,75 м³ в час).

10. В мензурке (цилиндрический сосуд с делениями на кубические сантиметры) расстояние между двумя смежными делениями 1,8см. Найти внутренний диаметр мензурки.

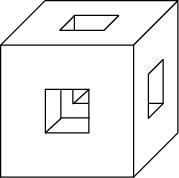11. В каждой грани медного куба с ребром 6 см проделали сквозное квадратное отверстие со стороной квадрата 2 см. Найдите вес оставшейся части, считая плотность меди приблизительно равным 0,9 г/см³.

12. Инженер, рост которого 180см пришел рассмотреть новую сферическую цистерну для хранения воды. Он забрался в пустую цистерну, и, когда он поднялся на место, находящееся в 5м 40см над точкой, в которой цистерна упирается на землю, его голова коснулась верхнего края цистерны. Зная, что город потребляет в час 40тысяч литров воды, он немедленно рассчитал, на сколько часов может хватить полной цистерны. Как он это сделал и как он получил результат.

Ответы

1. 2446625м³

1. 

2. 6см

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

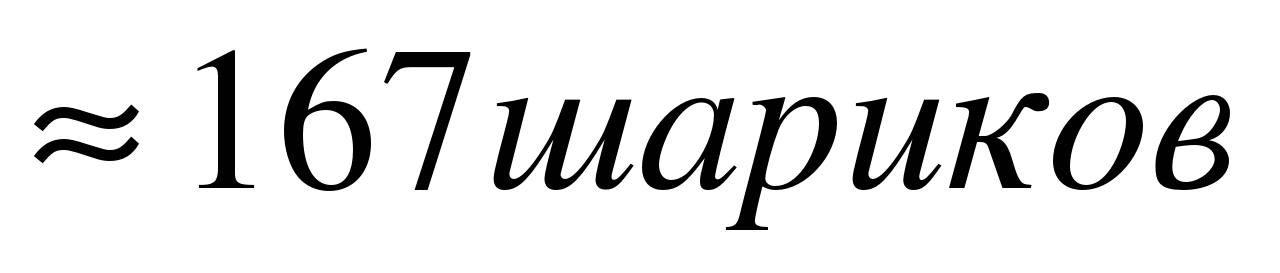
1. не переполнит

2. 

3. низкую банку.

4. 

5. 

6. 

7. 

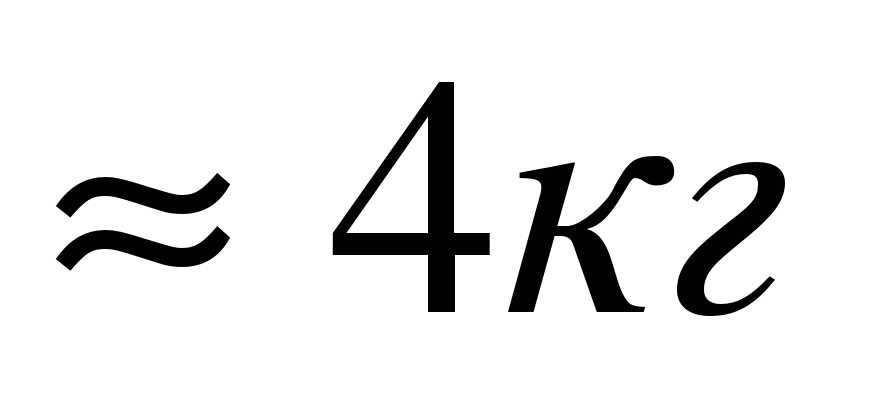
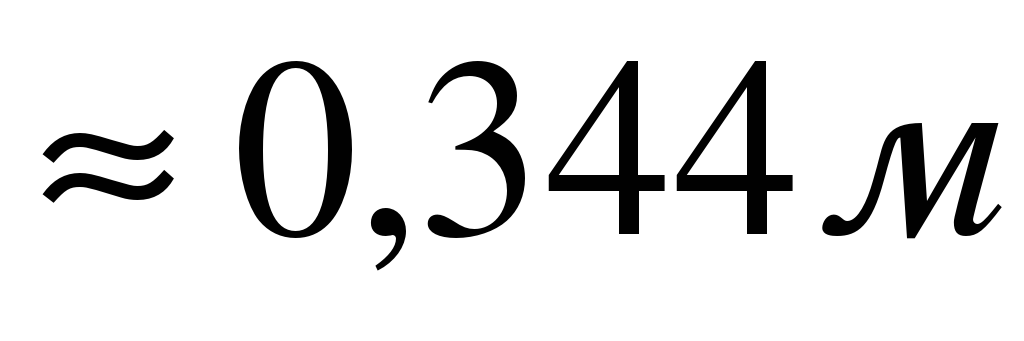
8. 10см

9. 40м³

10. 48л

11. 90 досок

12. 27 шариков

13. 11,5см

14. 1766,25см³

15. 24 машины

16. 1см

17. 3рабочих

18. 4мм

19. 144г

20. 5часов