Презентация "Решение неравенств методом интервалов"

Проверка д/з (на доске)

• № 327(б)
• № 329(б)
• № 335(б)
• № 336(б)

Класс в это время работает устно

(Задания для подготовки к ГИА по математике)

1

3

2

у

Используя график функции

а) охарактеризуйте знак первого коэффициента а и дискриминанта;

б) назовите значения переменной х , при которых функция принимает значения,

- равные нулю,

- положительные значения,

- отрицательные значения.

-6

-1

х

о

у

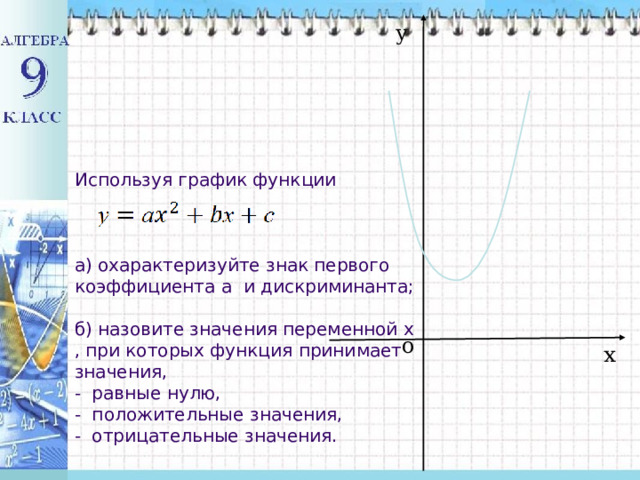
Используя график функции

а) охарактеризуйте знак первого коэффициента а и дискриминанта;

б) назовите значения переменной х , при которых функция принимает значения,

- равные нулю,

- положительные значения,

- отрицательные значения.

о

х

у

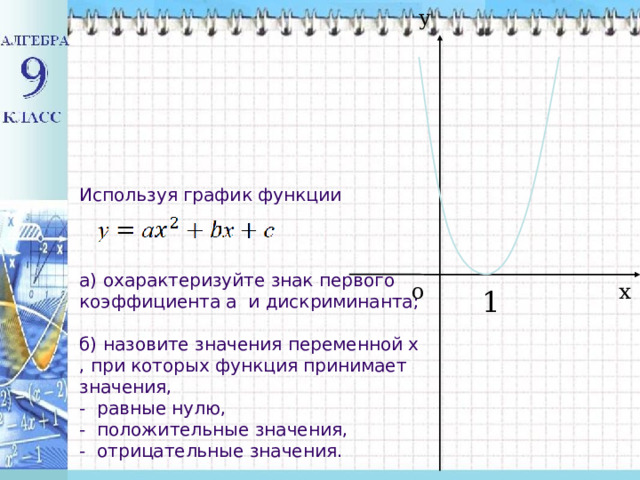
Используя график функции

а) охарактеризуйте знак первого коэффициента а и дискриминанта;

б) назовите значения переменной х , при которых функция принимает значения,

- равные нулю,

- положительные значения,

- отрицательные значения.

х

о

1

у

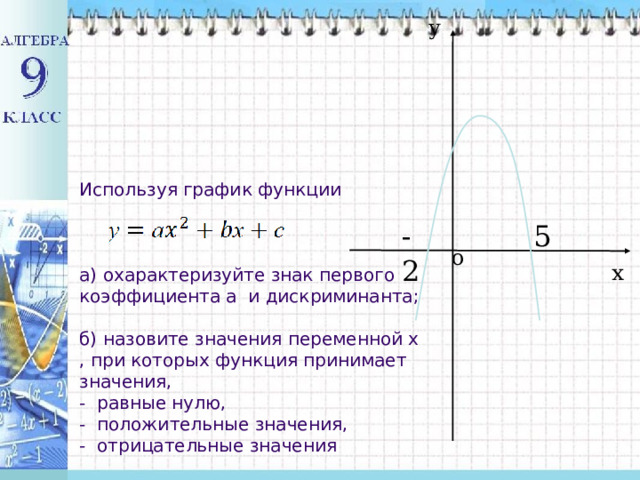
Используя график функции

а) охарактеризуйте знак первого коэффициента а и дискриминанта;

б) назовите значения переменной х , при которых функция принимает значения,

- равные нулю,

- положительные значения,

- отрицательные значения

-2

5

о

х

Решаем неравенства :

1.

Все действия на слайде – последовательно щелчком мышки.

х

-4

Ответ:

8

8

13х - 1 2 . Решение : 5х + 6х – 3 13х – 1 5х + 6х – 13х 3 – 1 -2х 2 (: (-2)) х -1 \\\\\\\\\\\\\\\\\ Ответ: (-∞; -1) x " width="640"

5х + 3(2х – 1) 13х - 1

2 .

Решение : 5х + 6х – 3 13х – 1

5х + 6х – 13х 3 – 1

-2х 2 (: (-2))

х

-1

\\\\\\\\\\\\\\\\\

Ответ: (-∞; -1)

x

Алгоритм решения неравенств методом интервалов

• Разложить многочлен на простые множители;
• Найти корни многочлена;
• Изобразить их на числовой прямой;
• Разбить числовую прямую на интервалы;
• Определить знаки множителей на интервалах знакопостоянства;
• Выбрать промежутки нужного знака;
• Записать ответ (с помощью скобок или знаков неравенства).

Самостоятельная работа

Вариант 1.

Вариант 2.

Решите неравенства методом интервалов:

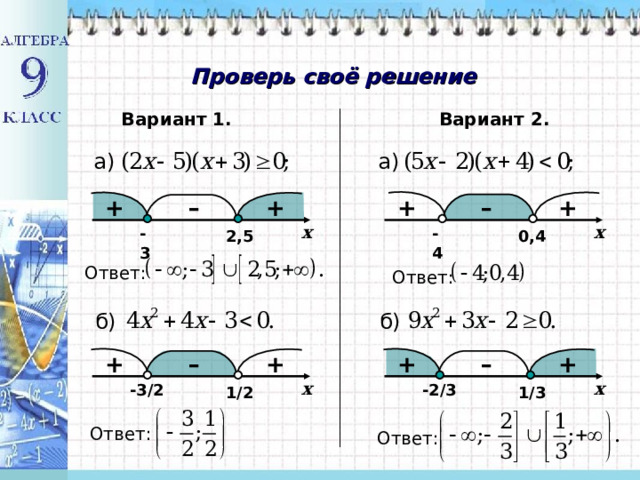
Проверь своё решение

Вариант 2.

Вариант 1.

а)

а)

+

–

+

–

+

+

x

x

-4

-3

0,4

2,5

Ответ:

Ответ:

б)

б)

+

+

–

+

+

–

x

x

-3/2

-2/3

1/3

1/2

Ответ:

Ответ:

1

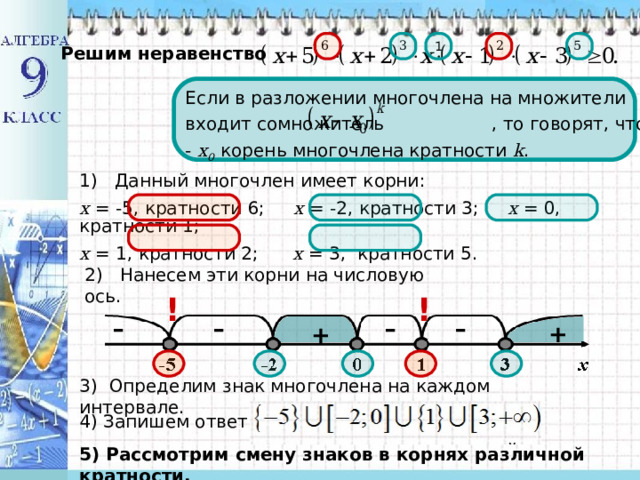
Решим неравенство

Если в разложении многочлена на множители входит сомножитель , то говорят, что - х 0 корень многочлена кратности k .

1) Данный многочлен имеет корни:

x = -5, кратности 6; x = -2, кратности 3; x = 0, кратности 1;

x = 1, кратности 2; x = 3, кратности 5.

2) Нанесем эти корни на числовую ось.

!

!

–

–

–

–

+

+

3) Определим знак многочлена на каждом интервале .

4) Запишем ответ:

5) Рассмотрим смену знаков в корнях различной кратности.

Обобщая ваши наблюдения, делаем выводы:

• Для решения неравенства важно знать, является ли k четным или нечетным числом

• При четном k многочлен справа и слева от х 0 имеет один и тот же знак (знак многочлена не меняется)

• При нечетном k многочлен справа и слева от х 0 имеет противоположные знаки (знак многочлена изменяется)
• При нечетном k многочлен справа и слева от х 0 имеет противоположные знаки (знак многочлена изменяется)

Решите неравенство

1 вариант:

2 вариант:

Сделайте выводы о смене знака на интервалах, в зависимости от степени кратности корня.

Оценка самостоятельной работы

За каждый верно выполненный пример – поставьте 1 балл.

0-1 баллов – необходимо еще тренироваться

2-3 балла – удовлетворительно

4 балла – хорошо

5 баллов – отлично

Домашнее задание

П.15

№ 332 (а), № 337 (а), №338 (в),

доп. №379, 381(а)

Использованные источники

• Учебник: Алгебра-9 класс, Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, М.: Просвещение, 2009.

2. Рурукин А.Н., Полякова С.А., Поурочные разработки по алгебре: 9 класс. – М.: ВАКО, 2010 – (В помощь школьному учителю).