Презентация "Применение приёмов технологии критического мышления на уроках математики в рамках реализации ФГОС"

МКОУ СОШ с.Утманово Подосиновского района Кировской области Применение приёмов технологии критического мышления на уроках математики в рамках реализации ФГОС

Автор: Семенова Людмила Александровна, учитель математики первой категории

  «Ребенок, никогда не познавший радости труда в учении, не переживший гордости от того, что трудности преодолены, - это несчастный человек»,-

Технология развития критического мышления

Руководствуясь новыми государственными документами, на сегодняшний день в качестве важнейшей задачи основного среднего образования выделяется формирование универсальных (метапредметных) учебных действий обеспечивающих обучающимся умение учиться, способность к самостоятельной работе, а, следовательно, и способность к саморазвитию и самосовершенствованию.

Требования, предъявляемые к выпускнику школы, не могут быть достигнуты без хорошо развитого мышления.

Главная цель технологии развития критического мышления - развитие интеллектуальных способностей ученика, позволяющих ему учиться самостоятельно.

Что дает ТРКМ ученику:

• повышение эффективности восприятия информации;
• повышение интереса как к изучаемому материалу, так и к самому процессу обучения;
• умение ответственно относиться к собственному образованию;
• умение работать в сотрудничестве с другими;
• повышение качества образования;
• желание и умение стать человеком, который учится в течение всей жизни.

Учитель, владеющий технологией развития критического мышления , способен:

• создать условия для развития личности, способной критически мыслить,
• проектировать пути и способы достижения поставленных задач,
• анализировать собственную деятельность;
• использовать разнообразный комплекс методов и приёмов ТРКМ, так как данная технология является общепедагогической, личностно-ориентированной и позволяет решать широкий спектр образовательных задач: обучающих, воспитательных и развивающих.

Приёмы обучения в технологии развития критического мышления

Приём «МОЗГОВОЙ ШТУРМ»

(МОЗГОВАЯ АТАКА)

Его цель — организация коллективной мыслительной деятельности по поиску нетрадиционных путей решения проблем.

Пример   использования   приёма   «Мозговой  штурм»    в 6 классе по теме «Сложение и вычитание отрицательных чисел»

Ситуация:  

Над  Компанией  нависла  угроза банкротства.  Компания будет объявлена банкротом в  случае  невыполнения следующего задания:

  Докажите, что значения данных выражений:

  а) (5 – 17) + 3 ; б) (– 26 – 54)( – 23 + 13)

в) ( – 15 + 12 ) + (– 6)

являются натуральными числами.

Спасите Компанию.

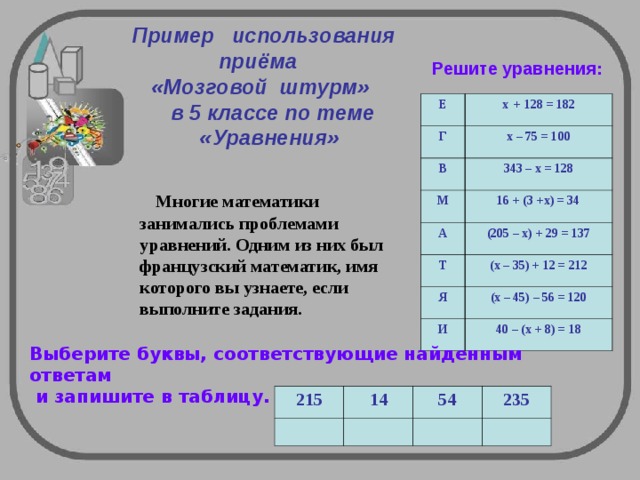
Пример   использования  

приёма   «Мозговой  штурм»    в 5 классе по теме «Уравнения»

Решите уравнения :

Е

х + 128 = 182

Г

х – 75 = 100

В

343 – x = 128

М

16 + (3 +х) = 34

А

(205 – х) + 29 = 137

Т

(х – 35) + 12 = 212

Я

(х – 45) – 56 = 120

И

40 – ( x + 8) = 18

Многие математики занимались проблемами уравнений. Одним из них был французский математик, имя которого вы узнаете, если выполните задания.

Выберите буквы, соответствующие найденным ответам

и запишите в таблицу.

215

14

54

235

Пример   использования   приёма   «Мозговой  штурм»    в 5 классе по теме «Возведение числа в квадрат»

Великий греческий математик Пифагор имел к числам особенное отношение, присваивал каждому числу какой-либо символ, например, «5» - символ цвета, «6» - холода, «7» обозначало разум и здоровье, «8» - любовь и дружбу. Именно Пифагор разделил все числа на четные и нечетные. А сейчас вы попробуйте повторить открытие, сделанное Пифагором.

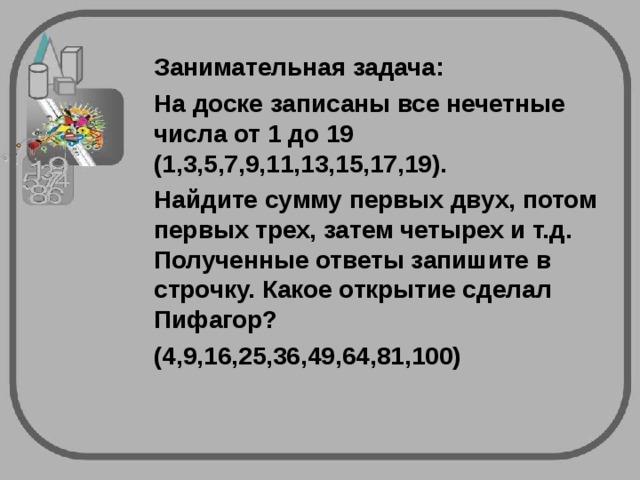
Занимательная задача:

На доске записаны все нечетные числа от 1 до 19 (1,3,5,7,9,11,13,15,17,19).

Найдите сумму первых двух, потом первых трех, затем четырех и т.д. Полученные ответы запишите в строчку. Какое открытие сделал Пифагор?

(4,9,16,25,36,49,64,81,100)

Пример   использования  

приёма «Мозговой  штурм» по теме  « Сложение и вычитание десятичных дробей »  

С давних времен разные растения, деревья и кустарники люди наделяли определенной символикой. Так, например, лавр символизирует славу, олива – мир.

Выполните вычисления с определением соответствия чисел и растений. По совпадающим ответам выясните, какие деревья символами каких качеств являются:

Лиственница

2,6 + 0,42 = ?

Щедрость

2 + 3,2 = ?

Сосна

0,25 + 18 = ?

Смелость

4 – 0, 98 = ?

Грецкий орех

7,5 – 1,8 = ?

Верность

0,25 + 2,25 + 15,5 = ?

Рябина

10 – 8,5 = ?

Грация

10 – 3,2 = ?

Апельсин

8,6 – 3,4 = ?

Стойкость

2,2 + 1,6 = ?

Вишня

4 – 0,2 = ?

Благоразумие

0,75 + 0,75 = ?

Береза

5,6 + 3,4 – 2,2 = ?

Хитрость

(придумать свой пример)

Карточки с названиями деревьев расставить по алфавиту

ОТВЕТЫ :

• лиственница – смелость,
• сосна – верность,
• рябина – благоразумие,
• апельсин – щедрость,
• вишня – стойкость,
• берёза – грация,
• грецкий орех ( ) символизирует хитрость

Приём « Лови ошибку »    6 класс, тема: «Уравнения»

При объяснении нового материала учитель решает сам уравнение, а учащиеся прилежно списывают:

2 * (4х + 15) – 3 = 2х – 43;

8х + 15 – 3 = 2х – 43; ( явная ошибка )

8х + 12 = 2х – 43

8х + 2х = 12 – 43 ( скрытая ошибка ), естественно при проверке ответ не сходится, среди учащихся волнение. Учитель объявляет громко: « Найдите ошибку !».

Учащиеся анализируют предложенный текст, пытаются выявить ошибки, аргументируют свои выводы.

Пример   использования   приёма   « Лови ошибку »   в 6 классе по теме: «Уравнения»

• Найдите ошибки и подчеркните их.

а) 6у + (у – 1) = 2у – (2у – 26)

6у – у – 1 = 2у – 2у + 26

5у + 1 = 26

5у = 26 – 1

5у = 25

у = 25 + 5

б) 6у – (у – 1) = (2у + 26) – 2у

6у – у + 1 = 2у + 26 + 2у

5у + 1 = 4у + 26

6у = 30

• Найдите ошибки, исправьте их, вставьте пропущенные знаки и продолжите решение уравнения

14 – 3(2х – 5) = 3 – 2(х – 5)

14 + 6х – 15 = 3 … 2х … 10

Умение увидеть ошибку, указать ее причину и исправить всегда приводит к возрастанию активности учащихся на уроке.

Приём «ДО – ПОСЛЕ»

Описание: приём может быть использован на 1 этапе урока, как приём актуализации знаний учащихся или на этапе рефлексии

Приём формирует:

• умение прогнозировать события;
• умение соотносить известные и неизвестные факты;
• умение выражать свои мысли;
• умение сравнивать и делать вывод

В таблице из двух столбцов в начале урока заполняется часть "До", в которой учащиеся записывают свои предположения о теме урока, о решении задачи, могут записать гипотезу.

Часть "После" заполняется в конце урока, когда изучен новый материал, проведен эксперимент, прочитан текст и т.д.

Далее ученик сравнивает содержание "До" и "После" и делает вывод.

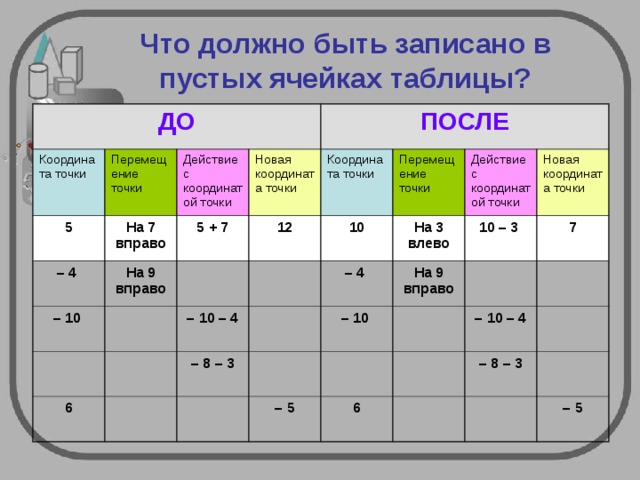
Что должно быть записано в пустых ячейках таблицы?

ДО

Координата точки

Перемещение точки

5

На 7 вправо

– 4

Действие с координатой точки

На 9 вправо

Новая координата точки

5 + 7

ПОСЛЕ

– 10

Координата точки

12

Перемещение точки

6

10

– 10 – 4

– 8 – 3

На 3 влево

Действие с координатой точки

– 4

На 9 вправо

Новая координата точки

10 – 3

– 10

7

– 5

– 10 – 4

6

– 8 – 3

– 5

Задания с рисунками

ДО - ПОСЛЕ

№ 658

(в, г, е, и, к, л)

ответ

Закрасьте каждую часть своего

рисунка цветом, соответствующим данной таблице

в

г

желтый

е

синий

зеленый

и

к

красный

л

черный

малиновый

Приём "Синквейн"

Это стихотворение из пяти строк, в котором автор выражает свое отношение к проблеме:

• 1 строка – одно ключевое слово, определяющее содержание синквейна;
• 2 строка – два прилагательных, характеризующих ключевое слово;
• 3 строка – три глагола, показывающие действия понятия;
• 4 строка – короткое предложение, в котором отражено авторское отношение к понятию;
• 5 строка – резюме: одно слово, обычно существительное, через которое автор выражает свои чувства и ассоциации, связанные с понятием.

Составление синквейна – индивидуальная работа, но для начала нужно составить его всем классом. Можно включить синквейн и в домашнее задание, тогда при проверке учитель оценит, насколько верно поняли учащиеся смысл изученного материала.

Пример   использования   приёма "Синквейн"  

• Треугольник

• Равнобедренный, равносторонний
• Строится, является, называется
• Сумма сторон треугольника –
• Периметр

• Дроби

• Правильные, неправильные
• Сравниваются, складываются, вычитаются
• У которых есть числитель и знаменатель
• Обыкновенные

Приём «Ромашка»

Делается цветок, на каждом лепестке, которого содержится пример или вопрос или указан термин, понятие. Каждый ученик отрывает по одному лепестку и решает пример или отвечает на вопрос или дает определение термину.

Приём «Верные и неверные утверждения».

Урок математики 6 класс по теме «Рациональные числа»:

• – 12 – число отрицательное? (да)
• 56 – число положительное? (да)
• При сложении отрицательных чисел получается число положительное (нет)
• – 13 + (– 15) = 28 (нет)
• – 5 + (– 24) = – 29 (да)
• Нуль больше любого отрицательного числа (да)
• Из двух отрицательных чисел то больше, модуль которого больше (нет)
• Из двух чисел то число больше, которое находится правее на координатной прямой (да)

Приём "Кластеры"

Прием "Кластеры" используется как на стадии вызова, так и на стадии рефлексии, т.е. может быть способом мотивации к размышлению до изучения темы или формой систематизирования информации при подведении итогов . В зависимости от цели  организуется индивидуальная или самостоятельная работа учащихся или коллективная – в виде общего совместного обсуждения. 

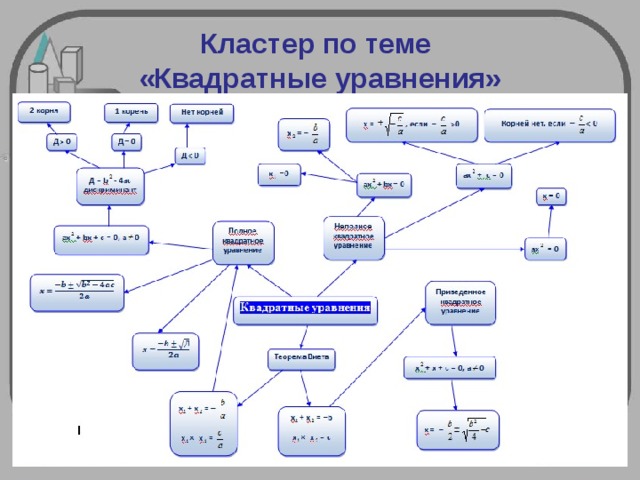
Кластер по теме «Квадратные уравнения»

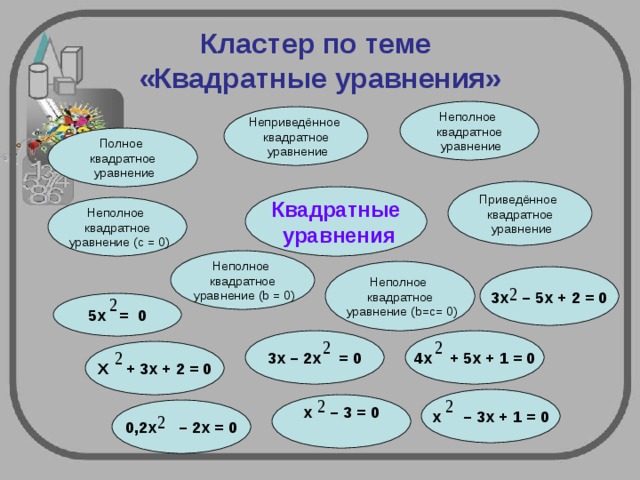
Кластер по теме «Квадратные уравнения»

Неполное

квадратное

уравнение

Неприведённое

квадратное

уравнение

Полное

квадратное

уравнение

Приведённое

квадратное

уравнение

Квадратные

уравнения

Неполное

квадратное

уравнение ( c = 0)

Неполное

квадратное

уравнение ( b = 0)

Неполное

квадратное

уравнение ( b=c= 0)

3х – 5х + 2 = 0

5х = 0

3х – 2х = 0

4х + 5х + 1 = 0

Х + 3х + 2 = 0

х – 3х + 1 = 0

х – 3 = 0

0,2х – 2х = 0

Применение данной технологии учителями в образовательном процессе даёт возможность учащимся овладеть УУД, так как ТРКМ позволяет решать задачи:

•   образовательной мотивации : повышения интереса к процессу учения и активного восприятия учебного материала;  
• информационной грамотности : развития способности к самостоятельной аналитической и оценочной работе с информацией любой сложности;

• социальной компетентности : формирования коммуникативных навыков и ответственности за знание.

Ценность данной технологии   и в том, что она учит: - детей слушать и слышать, - развивает речь, - даёт возможность общения, - активизирует мыслительную деятельность, познавательный интерес, - побуждает детей к действию, поэтому работают все. Уходит страх, повышается ответственность ученика за свой ответ, учитель и учащиеся вместе участвуют в добывании знаний.

Всё это необходимо не только на уроке математики. В этом заключается метапредметность данной технологии и её значимость.

«Ум ученика – это не сосуд, который надо заполнить знаниями, а факел, который надо зажечь»