Презентация по теме "Объёмы многогранников и круглых тел"

Урок по теме «Объемы тел» Стереометрия, 11 класс

МБОУ Школа № 31

Учитель: Кряквина Л.Н.

Содержание

• 1.Объем прямоугольного параллелепипеда и куба.
• 2.Объем прямой призмы.
• 3. Объем цилиндра.
• 4. Вопросы.
• 5. Задачи.

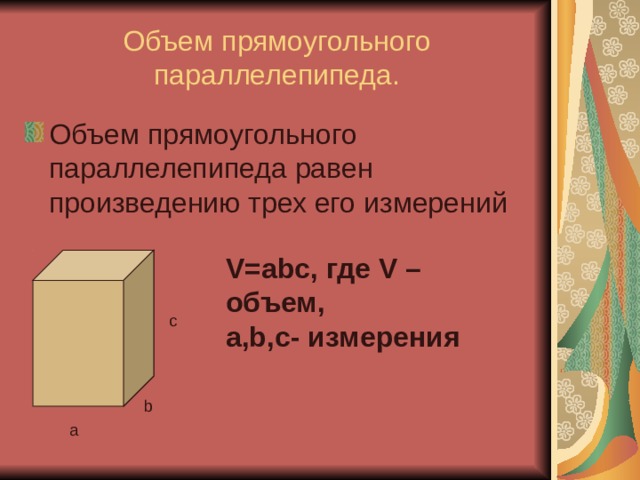
Объем прямоугольного параллелепипеда.

• Объем прямоугольного параллелепипеда равен произведению трех его измерений

V=abc , где V – объем,

a,b,c - измерения

c

b

a

Объем куба

Объем куба равен кубу длины

его ребра.

Например, если длина ребра

куба равна 5 единицам, то его

объем равен 125 единицам

кубическим.

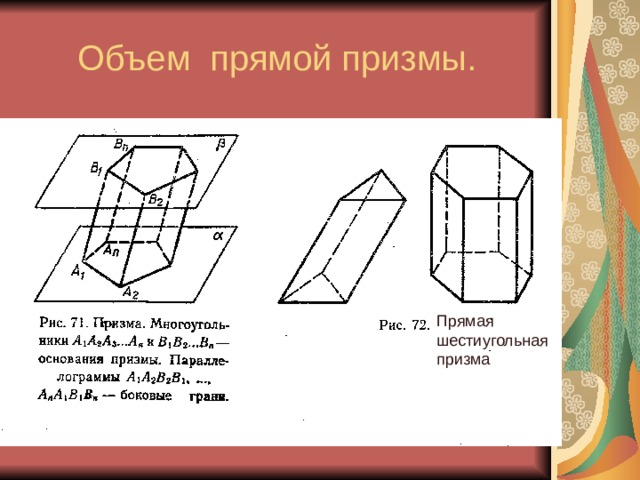
Объем прямой призмы.

Объем прямой призмы

равен произведению

площади основания

на высоту.

ABC -основание,

AD -высота

Призма называется прямой,

если ее боковые ребра

перпендикулярны плоскости

основания.

Прямая

шестиугольная

призма

Прямая

шестиугольная

призма

Объем прямой призмы

• Объем прямой призмы равен произведению площади основания призмы на высоту.
• Основание прямой призмы – многоугольник, высота равна длине бокового ребра.

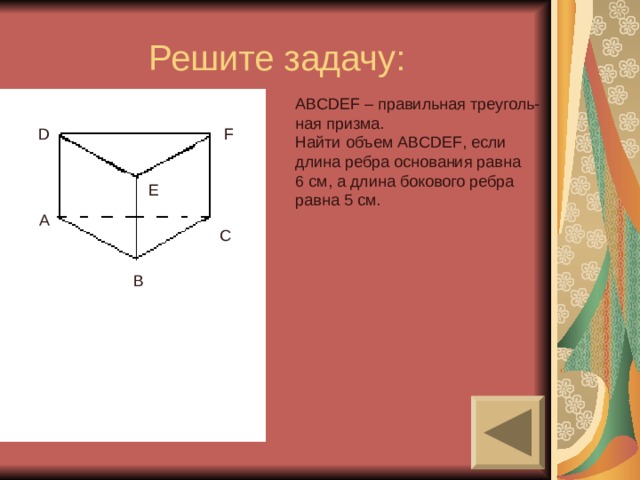
Решите задачу:

ABCDEF – правильная треуголь-

ная призма.

Найти объем ABCDEF , если

длина ребра основания равна

6 см, а длина бокового ребра

равна 5 см.

D

F

E

A

C

B

Объем цилиндра.

Объем цилиндра равен произведению площади

основания на высоту. В основании цилиндра лежит

круг, высотой является его образующая.

Осевым сечением цилиндра является прямоугольник.

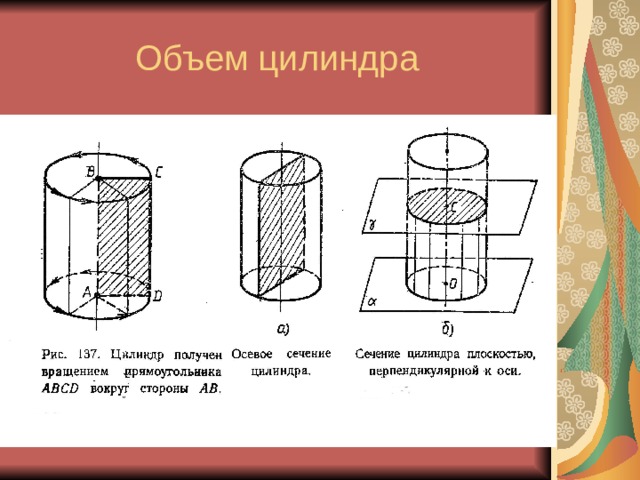
Объем цилиндра

Решите задачу:

Осевое сечение цилиндра – квадрат со стороной 6 см. Найти объем цилиндра.

Вопросы

• 1 .Чему равен объем прямоугольного параллелепипеда?
• 2.Чему равен объем куба?
• 3.Чему равен объем прямой призмы?
• 4.Чему равен объем цилиндра?

Задачи

Выберите правильный вариант ответа.

• 1. Объем куба равен 216 см 3 . Найти длину ребра куба.
• 1. 3 см
• 2. 4 см
• 3. 5 см
• 4. 6 см

Выберите правильный вариант ответа.

• 2. Стороны оснований и диагональ прямоугольного параллелепипеда относятся как 1:2:3. Длина бокового ребра равна 4. Найдите объем параллелепипеда. 1. 16 2. 20 3. 32 4. 64
• 2. Стороны оснований и диагональ прямоугольного параллелепипеда относятся как 1:2:3. Длина бокового ребра равна 4. Найдите объем параллелепипеда.
• 1. 16
• 2. 20
• 3. 32
• 4. 64

Выберите правильный вариант ответа.

• 3. Основанием прямой призмы служит прямоугольный треугольник с углом 30°. Расстояние от бокового ребра, проходящего через вершину прямого угла, до противолежащей боковой грани равно боковому ребру и равно 6. Найдите объем призмы.

• 1. 144
• 2. 144  3

• 3. 72  3

• 4. 72

Выберите правильный вариант ответа.

• 4. Площадь основания цилиндра равна 36  , а площадь осевого сечения – 120 . Найдите объем цилиндра .
• 1. 270 
• 2. 360 
• 3. 300 
• 4. 250 

Выберите правильный вариант ответа.

• 5. Диагональ прямоугольного параллелепипеда равна 8 и составляет с плоскостью основания угол в 30°, а с плоскостью боковой грани угол в 45°. Найдите объем параллелепипеда.

• 1. 64  2

• 2. 48  2

• 3. 3 2  2

• 4. 64

Выберите правильный вариант ответа.

• 6. Сечение цилиндра, параллельное его оси, отсекает от окружности основания дугу в 120°. Радиус основания цилиндра равен R , а угол между диагональю сечения и осью цилиндра равен 30°. Найдите объем цилиндра.
• 1. 3  R 3
• 2. 2  R 3
• 3.  R 3
• 4. 6  R 3

Задача решена верно !

К сожалению, Ваш ответ неверен.