Презентация по геометрии для 8 класса "Средняя линия треугольника"

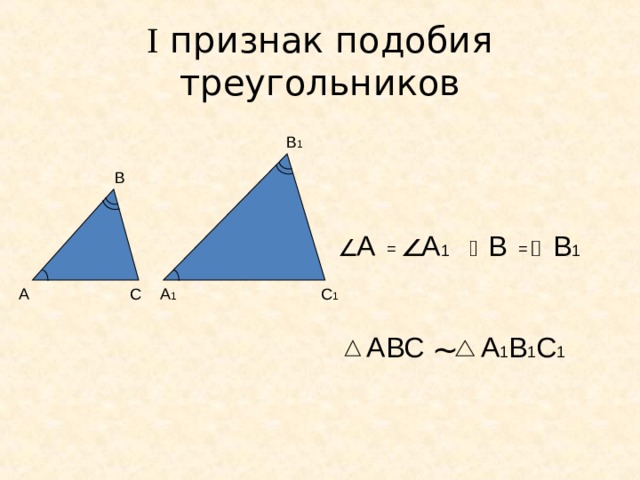
I признак подобия треугольников

В 1

В

В

А

В 1

А 1

=

=

С 1

А

С

А 1

~

А 1 В 1 С 1

АВС

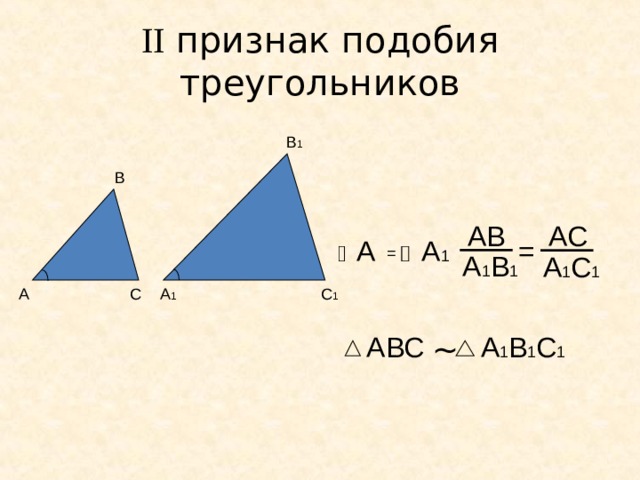
II признак подобия треугольников

В 1

В

АВ

A С

А

А 1

=

=

А 1 В 1

A 1 С 1

С 1

А 1

С

А

АВС

А 1 В 1 С 1

~

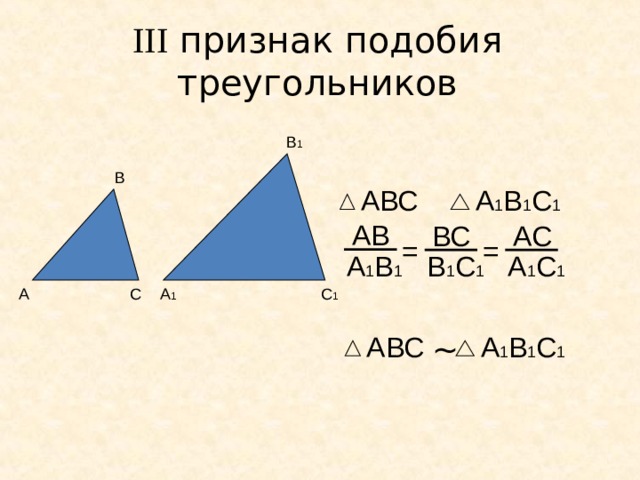
III признак подобия треугольников

В 1

В

АВС

А 1 В 1 С 1

АВ

АС

ВС

=

=

А 1 В 1

В 1 С 1

А 1 С 1

С 1

А 1

С

А

А 1 В 1 С 1

~

АВС

Дать определение средней линии треугольника.

Доказать теорему о средней линии треугольника.

Решать задачи, используя определение и свойство средней линии.

3

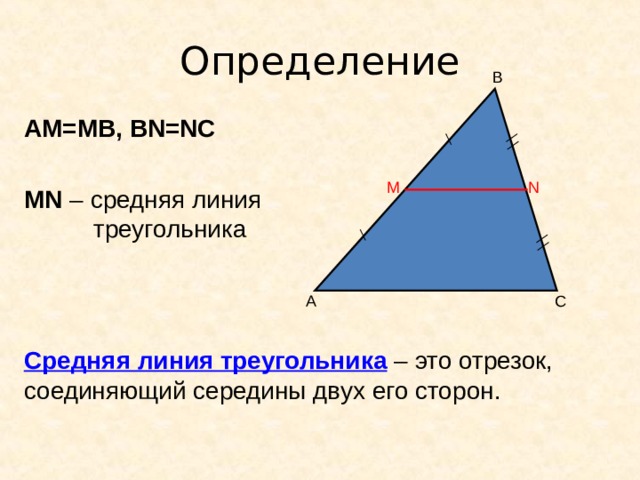
Определение

B

AM=MB, BN=NC

N

M

MN – средняя линия

треугольника

C

A

Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.

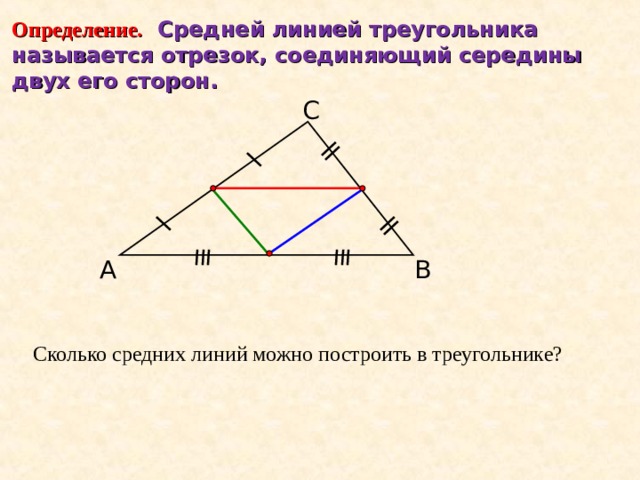
Определение. Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

С

В

А

Сколько средних линий можно построить в треугольнике?

8

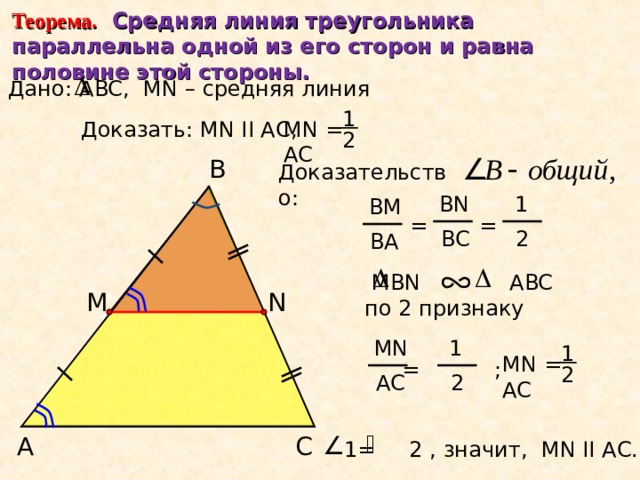
Теорема. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

ABC , М N – средняя линия

Дано:

1

MN = АС

Доказать: М N II АС,

2

B

Доказательство:

1

BN

BM

=

=

BC

2

BA

MBN ABC

по 2 признаку

М

N

1

MN

1

MN = АС

= ;

2

AC

2

C

А

1= 2 , значит, М N II АС.

9

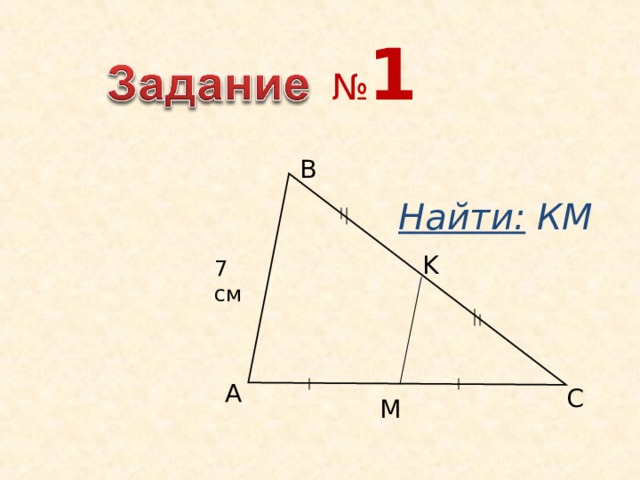
№ 1

B

Найти: КМ

K

7 см

A

C

M

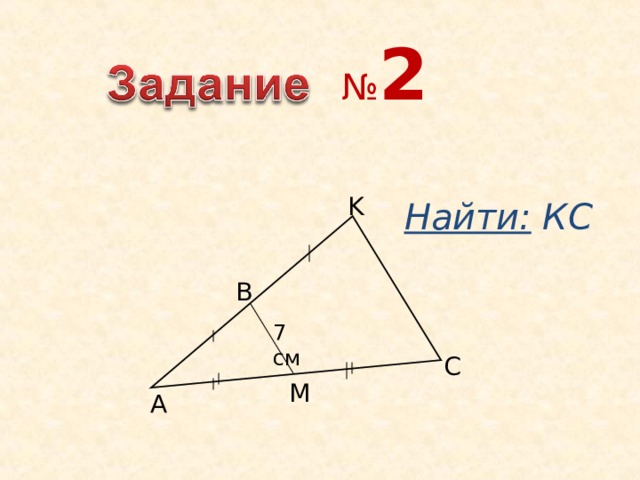
№ 2

Найти: КС

K

B

7 см

C

M

A

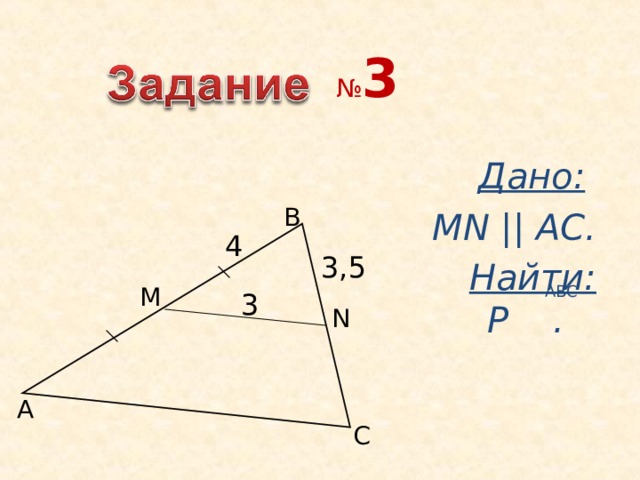
№ 3

Дано:

MN || AC .

Найти: Р .

B

4

3, 5

M

ABC

3

N

A

C

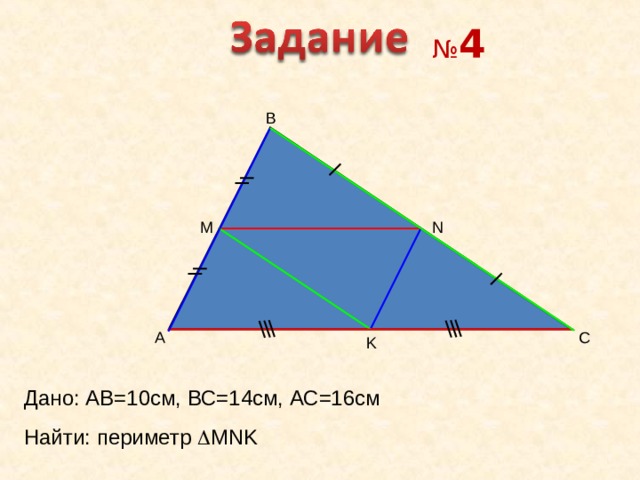
№ 4

B

M

N

A

C

K

Дано: AB=10c м, ВС=14см, АС=16см

Найти: периметр  MNK

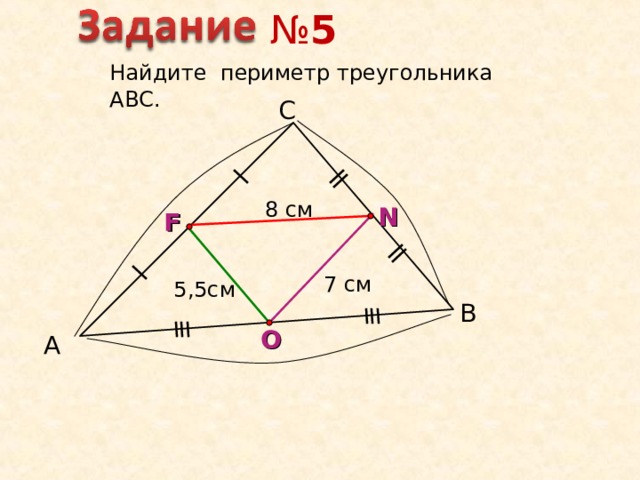
№ 5

Найдите периметр треугольника АВС.

С

8 см

N

F

7 см

5,5см

В

O

А

14

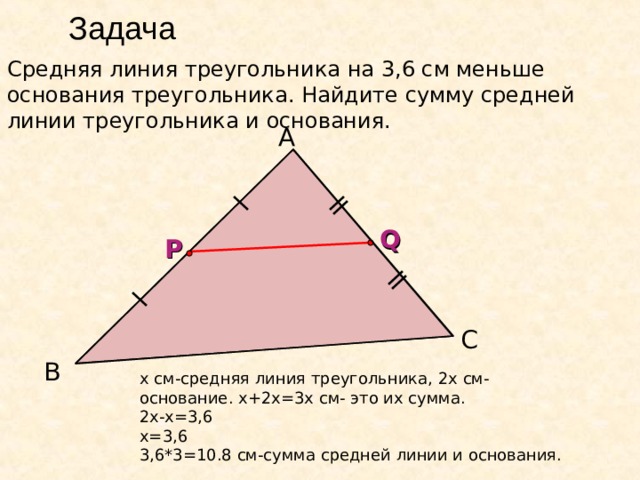
Задача

Средняя линия треугольника на 3,6 см меньше основания треугольника. Найдите сумму средней линии треугольника и основания.

А

Q

Р

Алтынов П.И. Геометрия. Тесты. 7-9 кл.

С

В

х см-средняя линия треугольника, 2х см- основание. х+2х=3х см- это их сумма. 2х-х=3,6

х=3,6

3,6*3=10.8 см-сумма средней линии и основания.  

15

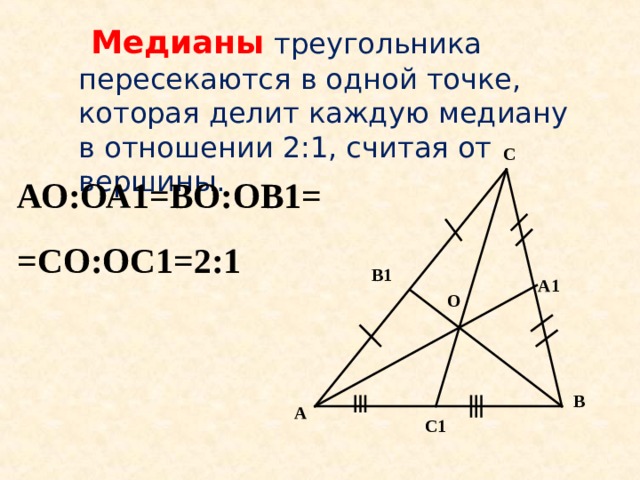
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

С

АО:ОА1=ВО:ОВ1=

=СО:ОС1=2:1

В1

А1

О

В

А

С1

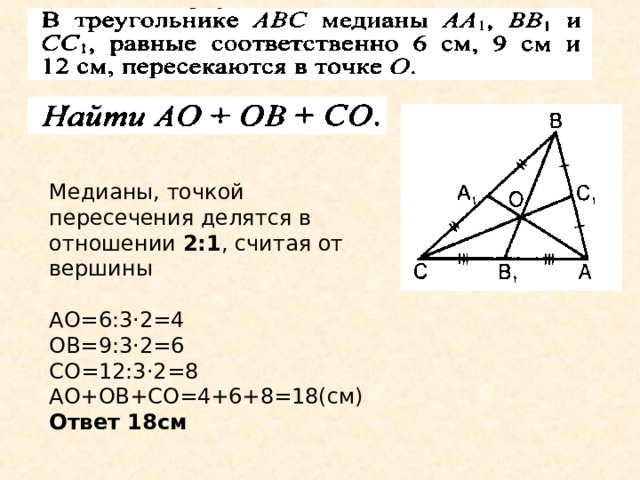
Медианы, точкой пересечения делятся в отношении 2:1 , считая от вершины

АО=6:3·2=4 ОВ=9:3·2=6 СО=12:3·2=8 АО+ОВ+СО=4+6+8=18(см) Ответ 18см

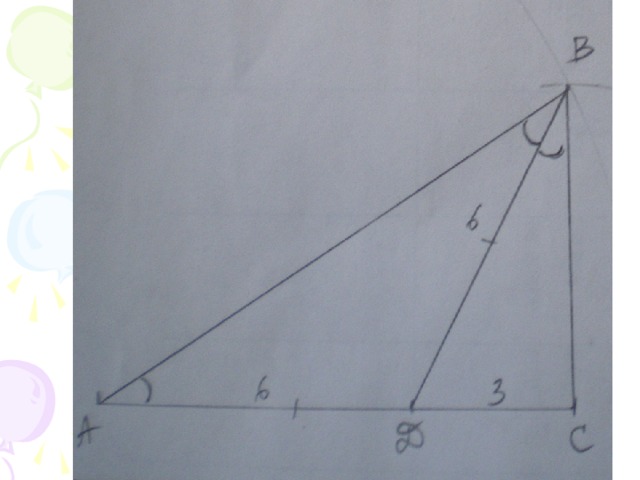
• Квадрат длины биссектрисы угла треугольника равен произведению сторон, из которых выходит биссектриса, без произведения отрезков, на которые она делит третью сторону.

Сначала найдем ВД.  По условию ∠АВС=2∠А, значит, ∠АВД=∠А, следовательно и ВД=АД=6 см. По свойству биссектрисы треугольника АД\ДС = АВ\ВС АВ\ВС=2; АВ=2ВС. Пусть ВС=х, тогда АВ=2х По свойству биссектрисы треугольника ВД²=АВ*ВС-АД*ДС 6²=2х*х-6*3 36=2х²-18 2х²=54 х²=27 х=3√3 ВС=3√3 см; АВ=2*3√3=6√3 см; АС=9 см.

• Какие новые знания получены на уроке?
• Что называют средней линией треугольника?
• Сформулируйте теорему о средней линии треугольника.
• Сформулируйте свойство медиан .

15

п.64,

№ 566

В раб тетр.

№ 61, 62, 63 ,64

15