Презентация на тему "Задачи матричной алгебры в пакетах символьной математики"

Задачи матричной алгебры в пакетах символьной математики

Выполнила : студентка группы МДМ-115 Дегтева К. С.

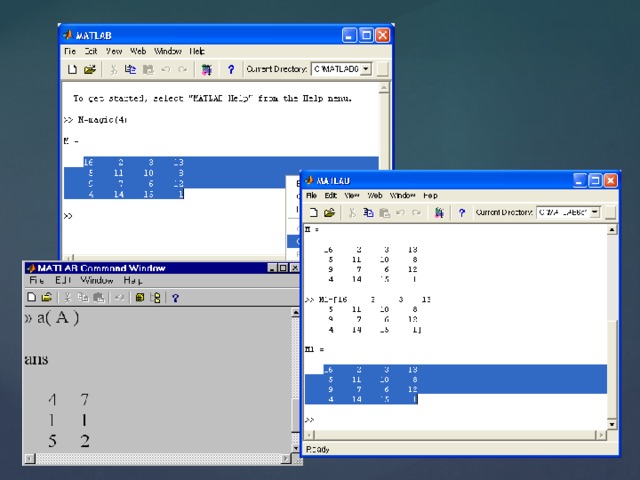
MatLab (сокращение от англ. «Matrix Laboratory») – пакет прикладных программ для решения задач технических вычислений и одноимённый язык программирования, используемый в этом пакете.

Первоначально MatLab предназначался для проектирования систем управления (основная специальность Джона Литтла), но быстро завоевал популярность во многих других научных и инженерных областях. Он также широко использовался и в образовании, в частности, для преподавания линейной алгебры и численных методов.

Основной особенностью языка MatLab является его широкие возможности по работе с матрицами, которые создатели языка выразили в лозунге «думай векторно» (англ. Think vectorized).

Библиотека MatLab позволяет пользоваться следующими категориями функций:

• операции с матрицами;
• сравнение матриц:
• решение линейных уравнений;
• разложение операторов и поиск собственных значений;
• нахождение обратной матрицы;
• поиск определителя;
• вычисление матричного экспоненциала;
• элементарная математика и т.д.

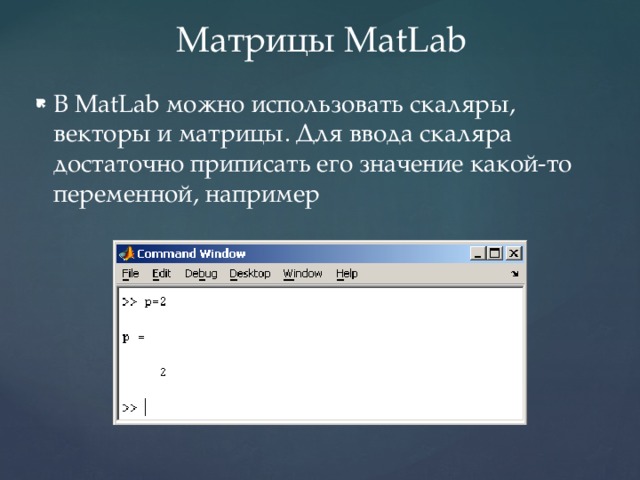
Матрицы MatLab

• В MatLab можно использовать скаляры, векторы и матрицы. Для ввода скаляра достаточно приписать его значение какой-то переменной, например

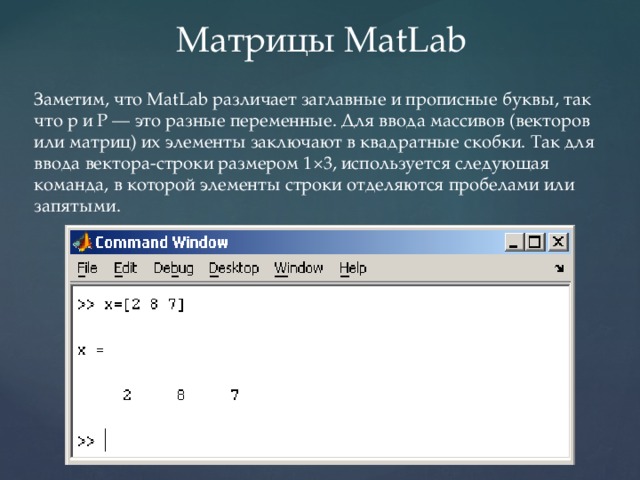
Матрицы MatLab

Заметим, что MatLab различает заглавные и прописные буквы, так что p и P — это разные переменные. Для ввода массивов (векторов или матриц) их элементы заключают в квадратные скобки. Так для ввода вектора-строки размером 1×3, используется следующая команда, в которой элементы строки отделяются пробелами или запятыми.

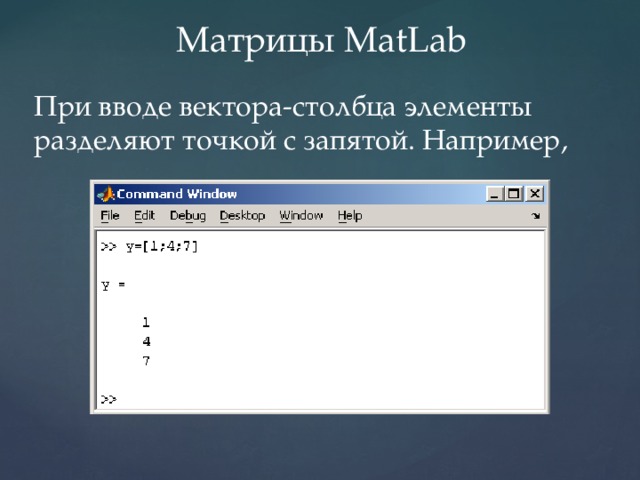
Матрицы MatLab

При вводе вектора-столбца элементы разделяют точкой с запятой. Например,

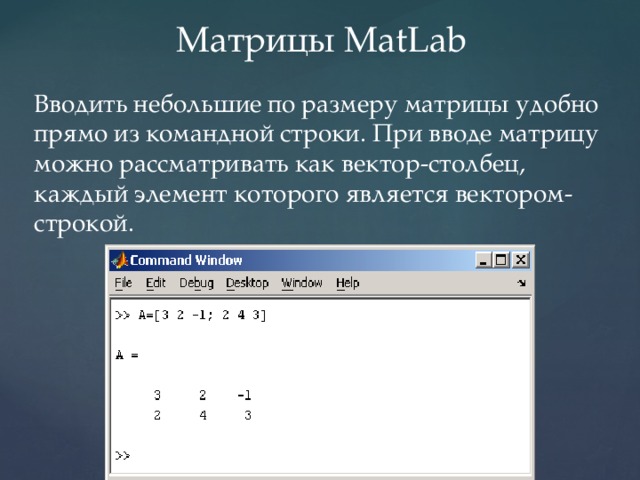
Матрицы MatLab

Вводить небольшие по размеру матрицы удобно прямо из командной строки. При вводе матрицу можно рассматривать как вектор-столбец, каждый элемент которого является вектором-строкой.

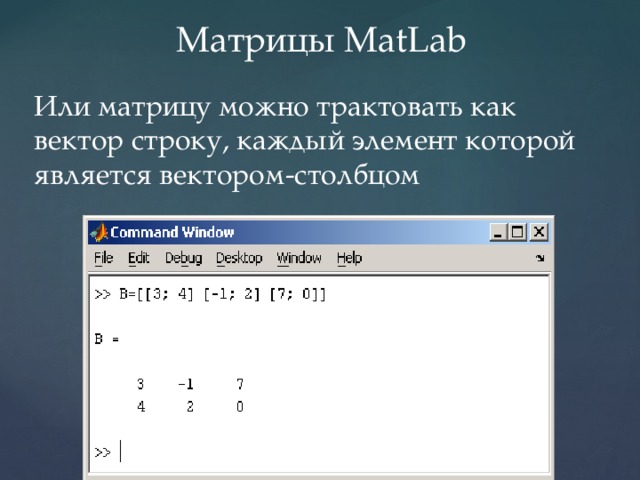
Матрицы MatLab

Или матрицу можно трактовать как вектор строку, каждый элемент которой является вектором-столбцом

Доступ к элементам

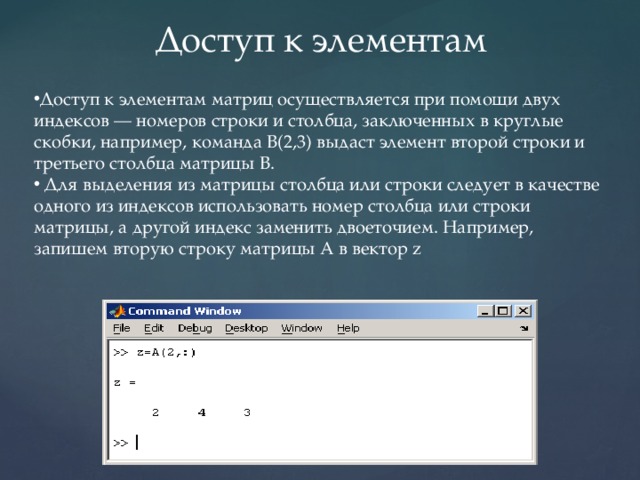
• Доступ к элементам матриц осуществляется при помощи двух индексов — номеров строки и столбца, заключенных в круглые скобки, например, команда B(2,3) выдаст элемент второй строки и третьего столбца матрицы B.
• Для выделения из матрицы столбца или строки следует в качестве одного из индексов использовать номер столбца или строки матрицы, а другой индекс заменить двоеточием. Например, запишем вторую строку матрицы A в вектор z

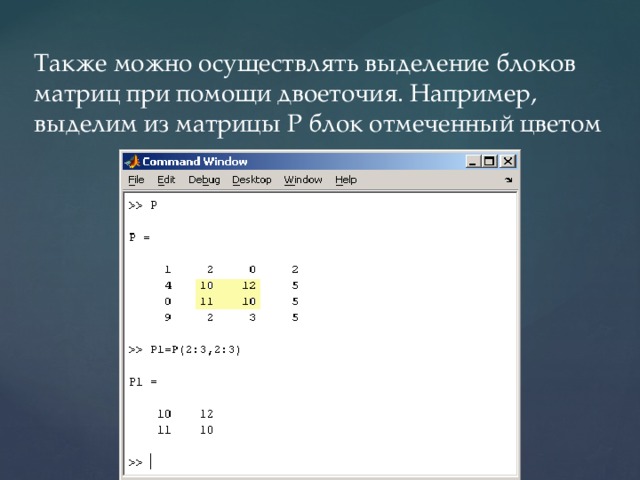
Также можно осуществлять выделение блоков матриц при помощи двоеточия. Например, выделим из матрицы P блок отмеченный цветом

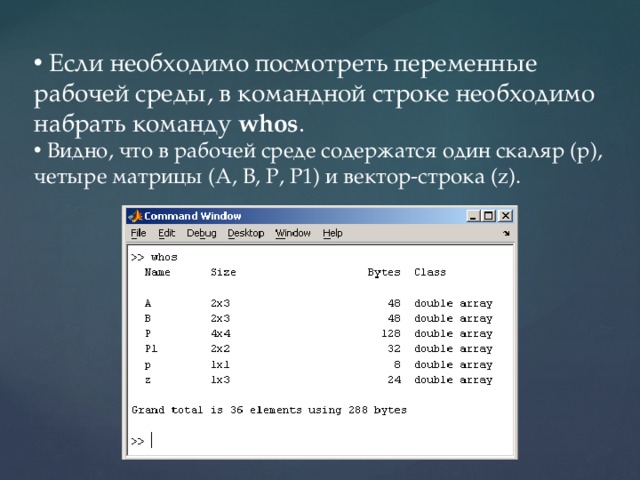
• Если необходимо посмотреть переменные рабочей среды, в командной строке необходимо набрать команду  whos .
• Видно, что в рабочей среде содержатся один скаляр (p), четыре матрицы (A, B, P, P1) и вектор-строка (z).

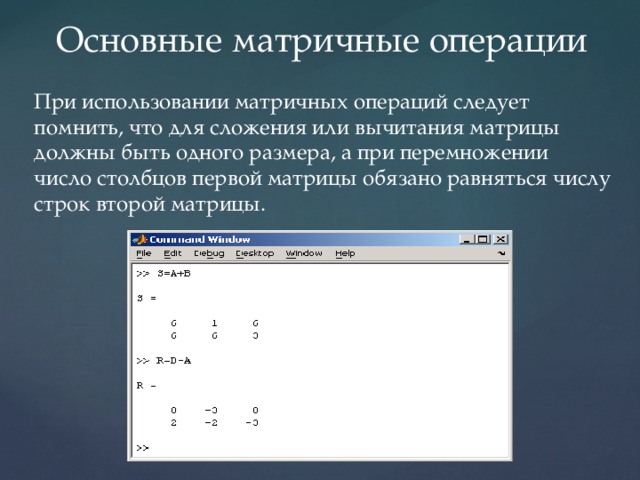
Основные матричные операции

При использовании матричных операций следует помнить, что для сложения или вычитания матрицы должны быть одного размера, а при перемножении число столбцов первой матрицы обязано равняться числу строк второй матрицы.

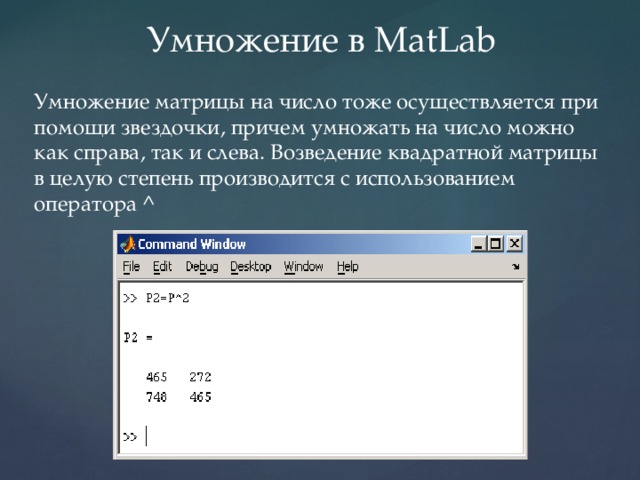
Умножение в MatLab

Умножение матрицы на число тоже осуществляется при помощи звездочки, причем умножать на число можно как справа, так и слева. Возведение квадратной матрицы в целую степень производится с использованием оператора ^

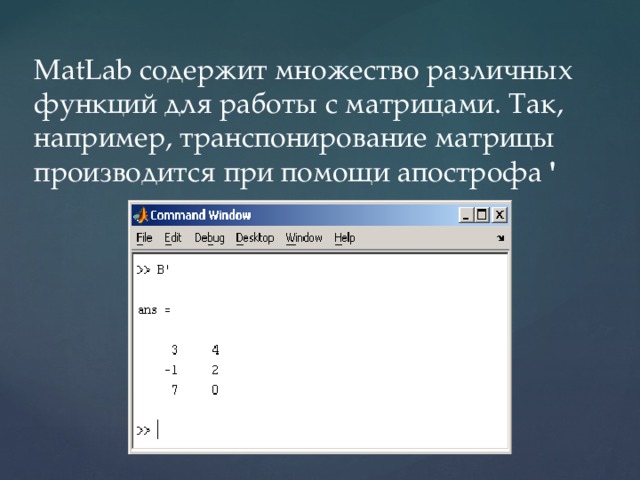
MatLab содержит множество различных функций для работы с матрицами. Так, например, транспонирование матрицы производится при помощи апострофа  '

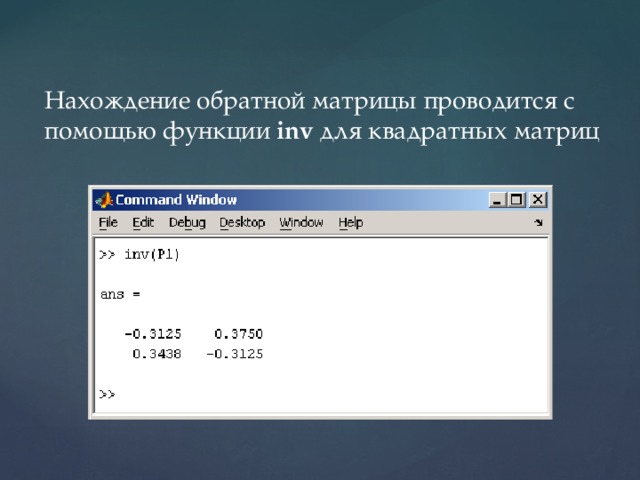
Нахождение обратной матрицы проводится с помощью функции  inv  для квадратных матриц

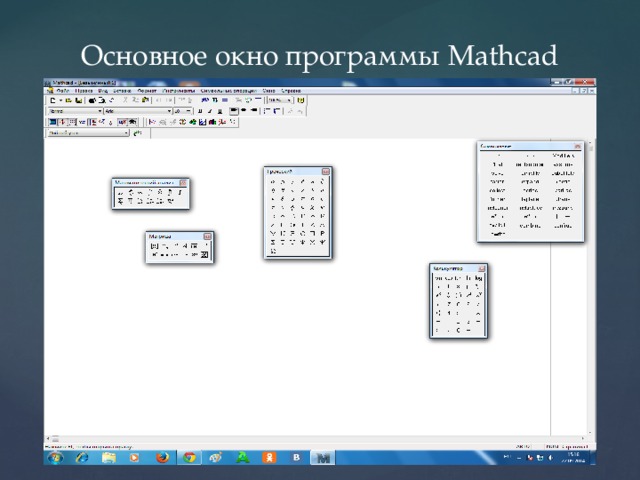
Основное окно программы Mathcad

Действия над матрицами в Mathcad. Панель матриц

Окно ввода Insetrt Matrix (ввести матрицу).

Шаблон матрицы

Над векторами определены показанные на рисунке операции сложения и вычитания, транспонирования, умножения по математическим правилам умножения матриц. Знак транспонирования следует вводить с панели Matrix (матрица). Порядковый номер элемента, который является его адресом, называется индексом. Нижняя граница индексации задается значением системной переменной ORIGIN, которая может принимать значение 0 или 1.

• Задача 1. Ввести все векторы рис.5 и произвести над ними все действия, проведенные на рисунке.
• Матрицы в Маткаде вводятся так же, как и векторы, но число столбцов в них больше единицы. Элементами матрицы могут быть также числа, буквы, выражения. Как и в случае векторов, буквенные элементы и элементы – выражения должны быть предварительно определены численно. На рисунке показаны различные способы ввода матриц.

Команды панели Matrix:

• кнопка индексации элементов матрицы,

• кнопка обращения матрицы,

• кнопка скалярного произведения векторов и матриц

• кнопка транспонирования матрицы,

• кнопка векторного произведения двух векторов

• кнопка сложения векторов

• кнопка выделения столбца матрицы

• кнопка вычисления детерминанта матрицы.