Презентация по математике "Второй признак равенства треугольников"

Повторение:

Равенство треугольников.

Два треугольника называются равными, если совмещаются наложением

Первый признак равенства (по двум сторонам и углу между ними)

Если две стороны и угол между ними одного треугольника соответственно равны сторонам и углу между ними другого треугольника, то такие треугольники равны.

Теорема:

Если сторона и два прилегающих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Дано: треугольник ABC, треугольник A₁B₁C₁

АВ = A₁B_1.

Второй признак равенства треугольников

Выполнила: учитель математики МОУ «Средняя школа № 36»

Суняйкина Е.К.

Повторение:

• Равенство треугольников

Два треугольника называются равными, если совмещаются наложением

• Первый признак равенства (по двум сторонам и углу между ними)

Если две стороны и угол между ними одного треугольника соответственно равны сторонам и углу между ними другого треугольника, то такие треугольники равны

Теорема: Если сторона и два прилегающих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

А1

В1

С1

А

В

С

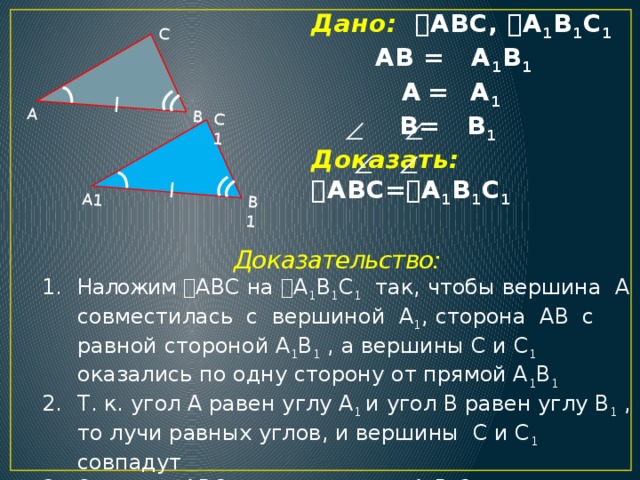
Дано:  ABC,  A 1 B 1 C 1 АВ = A 1 B 1 A = A 1 B= B 1 Доказать:  ABC=  A 1 B 1 C 1

Доказательство:

• Наложим  ABC на  A 1 B 1 C 1 так, чтобы вершина А совместилась с вершиной A 1 , сторона АВ с равной стороной A 1 B 1 , а вершины С и C 1 оказались по одну сторону от прямой A 1 B 1
• Т. к. угол А равен углу A 1 и угол В равен углу B 1 , то лучи равных углов, и вершины C и C 1 совпадут
• Значит,  ABC наложится на  A 1 B 1 C 1 , т. е.  ABC=  A 1 B 1 C 1

4

Решение задач

В

С

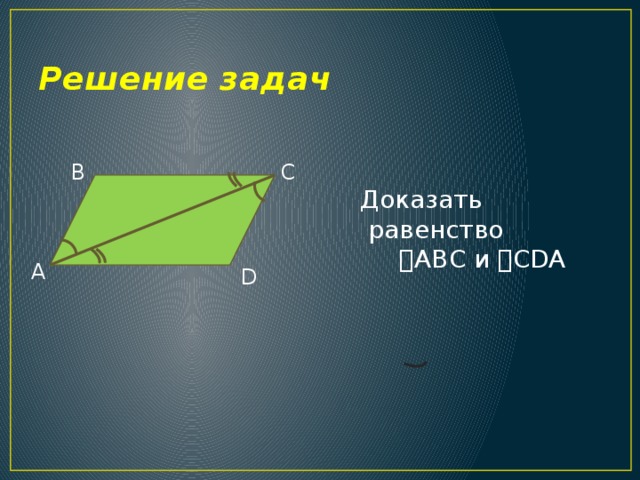
Доказать равенство

 AВС и  CDA

А

D

Решение задач

• Доказать равенство

А

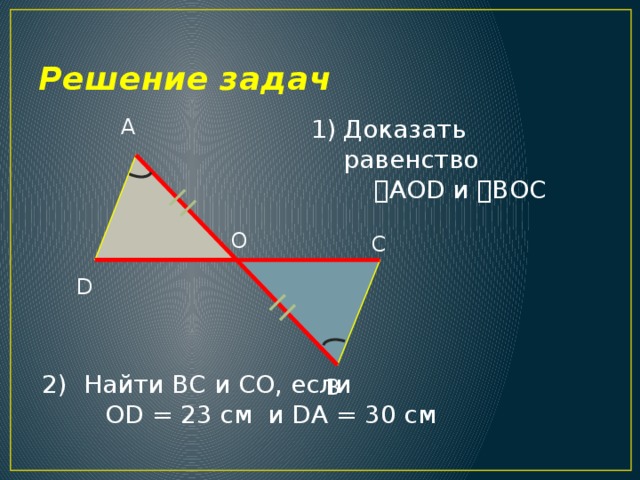
 AOD и  BОC

О

С

D

2) Найти ВС и СО, если

ОD = 23 см и DA = 30 см

В

Решение задач

• Доказать равенство

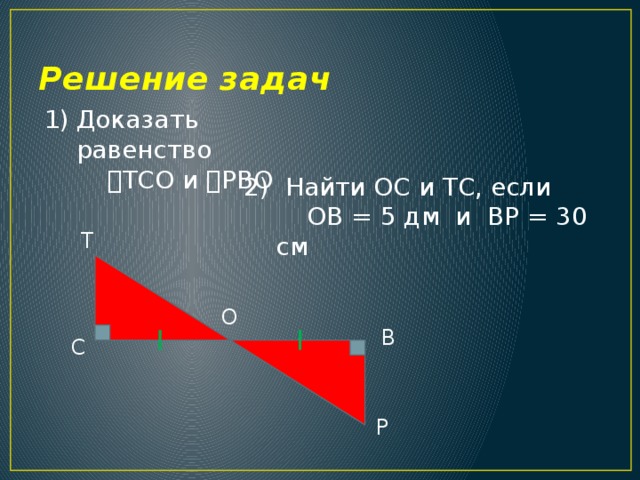
 ТСО и  РВО

2) Найти ОС и ТС, если

ОВ = 5 дм и ВР = 30 см

Т

О

В

С

Р

№ 126

Дано:

∟ DAB = ∟CBA, ∟CAB = ∟DBA, AC=13 см

Найти: BD.

Решение:

Рассмотрим ΔDBA и ΔCAB:

∟ DAB = ∟CBA - по условию задачи

∟ CAB = ∟DBA - по условию задачи

AB – общая сторона. ΔDBA = ΔCAB по стороне и двум прилегающим к ней двум углам.

Поэтому BD=AC как соответственные стороны равных треугольников. AC = 13 см, значит BD = 13 см.

Ответ: BD = 13 см

Самостоятельно

№ 121, 127

Домашнее задание

§ 19, ответить на вопрос 14.

№ 122-125