Третий признак равенства треугольников (по трём сторонам).
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
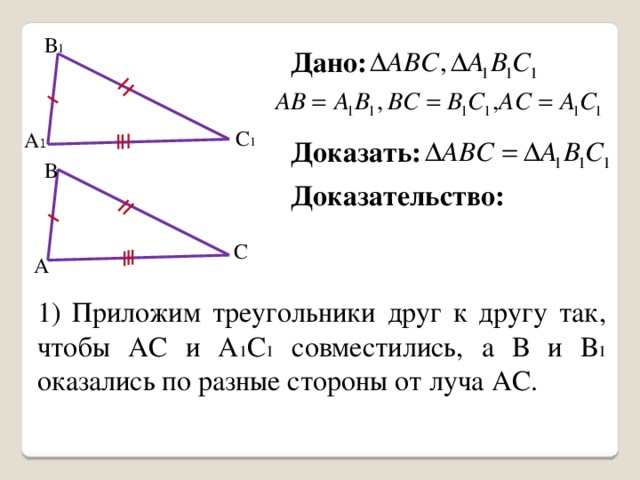
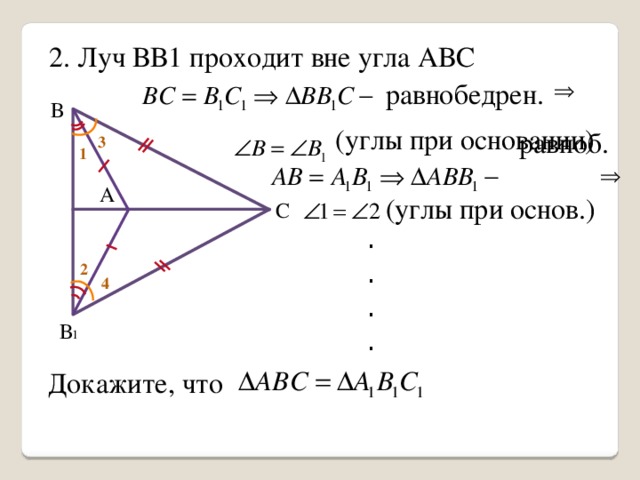
Дано: ΔABC, ΔA1B1C1
AB=A1B1, BC=B1C1, AC=A1C1
Доказать: ΔABC=ΔA1B1C1.
Доказательство:
1) Приложим треугольники друг к другу так, чтобы АС и А1С1 совместились, а В и В1 оказались по разные стороны от луча АС.
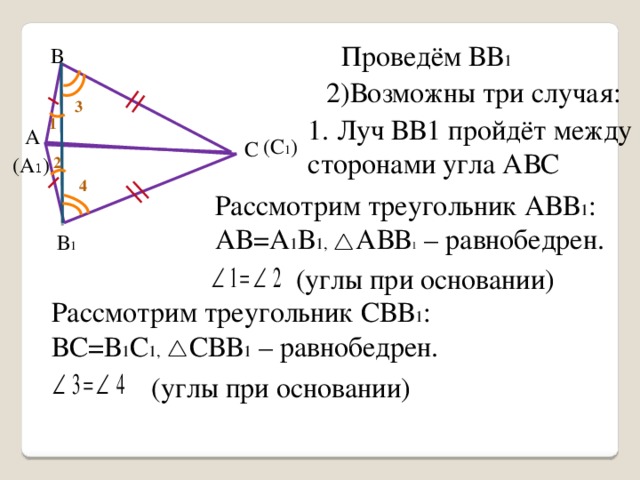
Проведём ВВ1
2) Возможны три случая:
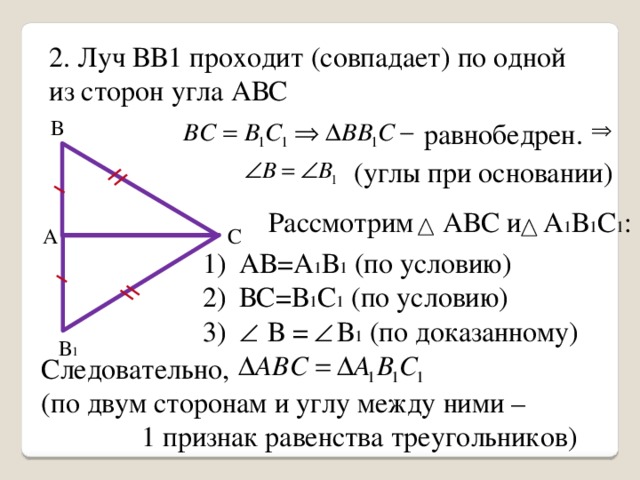
1. Луч ВВ1 пройдёт между сторонами угла АВС
Рассмотрим треугольник АВВ1:
АВ=А1В1, ΔАВВ1 – равнобедрен.
∠1=∠2 (углы при основании)
Рассмотрим треугольник СВВ1:
ВС=В1С1, ΔСВВ1 – равнобедрен.
∠3=∠4 (углы при основании)

 Получите свидетельство
Получите свидетельство Вход
Вход














 Презентация по математике "Третий признак равенства треугольников" (0.15 MB)
Презентация по математике "Третий признак равенства треугольников" (0.15 MB)
 0
0 2480
2480 419
419 Нравится
0
Нравится
0


