Презентация по математике "Решение задания С2 различными способами"

Презентация будет полезна учителям при подготовке учеников к ЕГЭ. В презентации рассматривается два способа решения задач С2 на нахождение площади сечения пирамиды плоскостью.

В правильной четырёхугольной пирамиде MABCD с вершиной М стороны основания равны 15, а боковые ребра равны 16. Найдите площадь сечения пирамиды плоскостью, проходящей через точку D и середину ребра MB параллельно прямой АС.

Обозначим точку пересечения медиан МО и DL треугольника MDB буквой Q.При этом L - середина отрезка MB, О - точка пересечения диагоналей основания, квадрата ABCD.

Через точку Q проведём прямую, параллельную прямой АС. Точки пересечения построенной прямой с рёбрами МА и МС обозначим Е и N соответственно.

Четырёхугольник DELN - сечение пирамиды плоскостью, проходящей через точку D и середину ребра MB параллельно прямой АС, поскольку по построению содержит прямую EN параллельную АС.

Задание С2

В правильной четырёхугольной пирамиде MABCD с вершиной М стороны основания равны 15, а боковые ребра равны 16. Найдите площадь сечения пирамиды плоскостью, проходящей через точку D и середину ребра MB параллельно прямой АС.

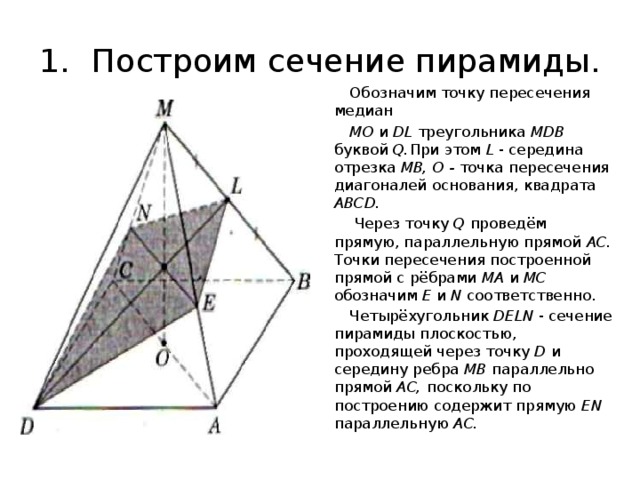
1. Построим сечение пирамиды.

Обозначим точку пересечения медиан

МО и DL треугольника MDB буквой Q. При этом L - середина отрезка MB, О - точка пересечения диагоналей основания, квадрата ABCD.

Через точку Q проведём прямую, параллельную прямой АС. Точки пересечения построенной прямой с рёбрами МА и МС обозначим Е и N соответственно.

Четырёхугольник DELN - сечение пирамиды плоскостью, проходящей через точку D и середину ребра MB параллельно прямой АС, поскольку по построению содержит прямую EN параллельную АС.

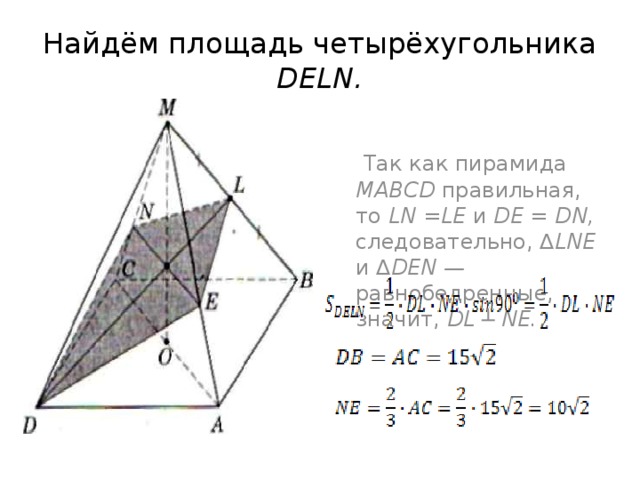
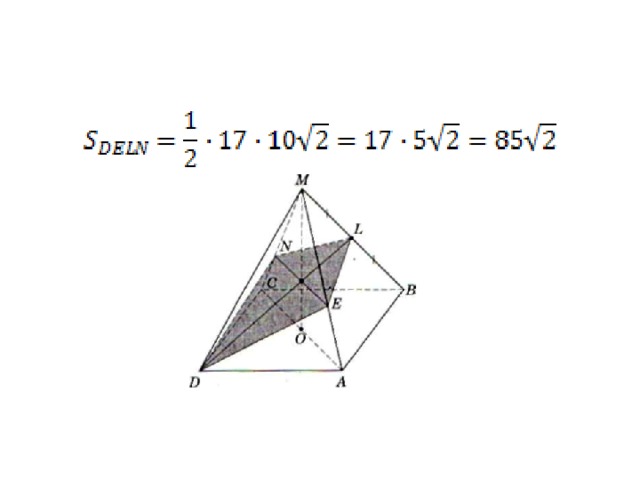
Найдём площадь четырёхугольника DELN.

Так как пирамида MABCD правильная, то LN =LE и DE = DN, следовательно, ∆ LNE и ∆ DEN — равнобедренные, значит, DL ┴ NE.

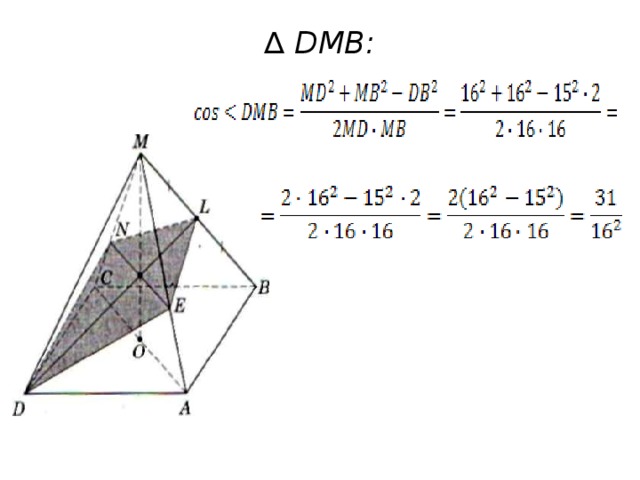
∆ DMB:

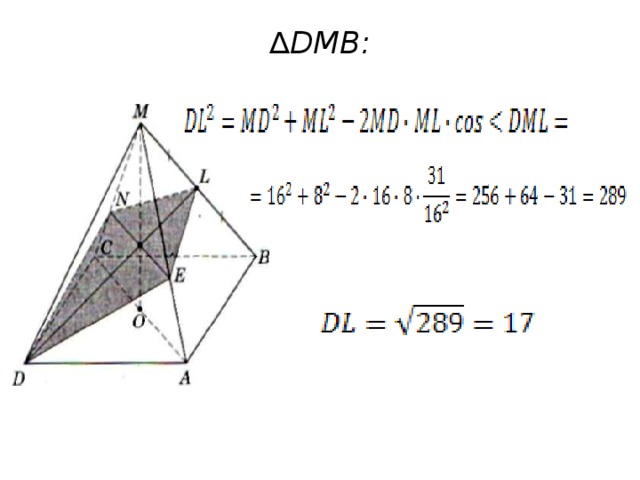
∆ DMB:

Еще одно возможное решение

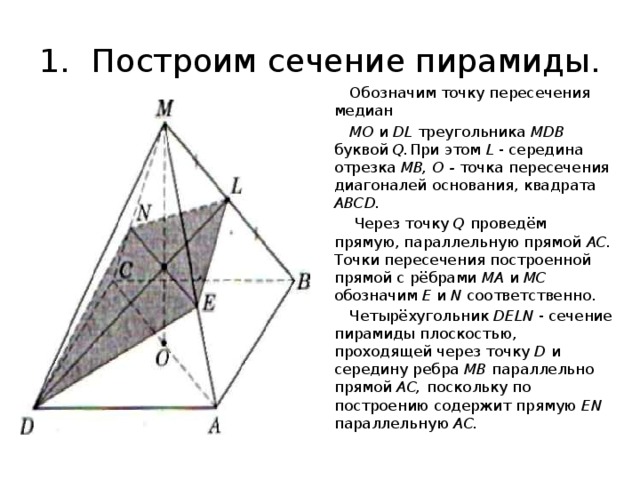
1. Построим сечение пирамиды.

Обозначим точку пересечения медиан

МО и DL треугольника MDB буквой Q. При этом L - середина отрезка MB, О - точка пересечения диагоналей основания, квадрата ABCD.

Через точку Q проведём прямую, параллельную прямой АС. Точки пересечения построенной прямой с рёбрами МА и МС обозначим Е и N соответственно.

Четырёхугольник DELN - сечение пирамиды плоскостью, проходящей через точку D и середину ребра MB параллельно прямой АС, поскольку по построению содержит прямую EN параллельную АС.

Найдём площадь четырёхугольника DELN.

Так как пирамида MABCD правильная, то LN =LE и DE = DN, следовательно, ∆ LNE и ∆ DEN — равнобедренные, значит, DL ┴ NE.

∆ DMB:

Основные ошибки

• Преимущественные ошибки в решении этого задания были связаны с определением фигуры, являющейся сечением пирамиды, — четырёхугольник DELN принимался и за ромб, и за прямоугольник.
• В обосновании перпендикулярности диагоналей четырёхугольника DELN выпускники ссылались на неверный гео­метрический факт: если прямые лежат в перпендикулярных плоскостях (в данном случае MAC и MDB) и пересекаются, то они перпендикулярны. Убедиться в ошибочности этого утверждения несложно - достаточно посмотреть на прямые AQ и DL, которые удовлетворяют условию утверждения, но не являются перпендикулярными.
• Треугольник MDB считали равнобедренным (MD = DB), и отрезок DL находили как медиану этого треугольника.
• Отрезок NE считали средней линией треугольника MAC, вследствие чего длину этого отрезка находили как половину диагонали АС.