Презентация по математике "Решение задач по теме "Трёхгранный угол""

«Где отсутствуют точные знания, там действуют догадки, а из 10 догадок- 9 ошибки.»

                    М. Горький.

Известно, что учащиеся средних школ хуже всего решают задачи по планиметрии и стереометрии. Планиметрия и стереометрия, теория которых основана на аксиоматическом походе, являются традиционно трудными для понимания учащимися. Эти разделы требуют отдельной и серьёзной подготовки выпускниками.

Решение  задач по стереометрии требуют хорошего пространственного воображения, умения строить ясные и чёткие чертежи, сводить решение стереометрической задачи к серии планиметрических задач.

Теорема косинусов  для трехгранного угла

Плоские углы трехгранного угла находятся в определенной зависимости с двухгранными его углами

Имеет место равенство:  cosα=cosβ*cosγ+sinβ *sinγ *cos A

Аналогичные формулы можно записать для cosβ и cosγ  

Приведенная формула угла (формула косинусов) позволяет по трем плоским углам найти двугранные углы при ребрах трехгранного угла  и, наоборот, зная все двугранные углы найти все плоские углы при вершине трехгранного угла.

Подготовка к ЕНТ. Решение задач по теме «Трехгранный угол»

Из опыта работы учителя математики

Соколовой В.А.

«Где отсутствуют точные знания, там действуют догадки, а из 10 догадок- 9 ошибки.»

М. Горький.

Известно, что учащиеся средних школ хуже всего решают задачи по планиметрии и стереометрии. Планиметрия и стереометрия, теория которых основана на аксиоматическом походе, являются традиционно трудными для понимания учащимися. Эти разделы требуют отдельной и серьёзной подготовки выпускниками.

• Решение задач по стереометрии требуют хорошего пространственного воображения, умения строить ясные и чёткие чертежи, сводить решение стереометрической задачи к серии планиметрических задач.

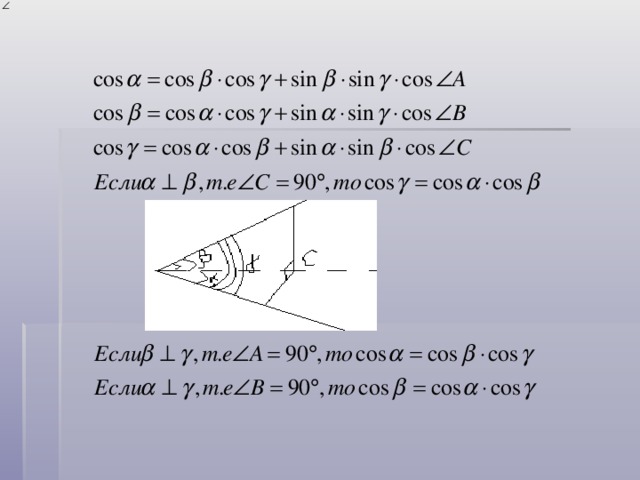
П лоские углы трехгранного угла находятся в определенной зависимости с двухгранными его углами

Имеет место равенство : cosα=cosβ*cosγ+sinβ *sinγ *cos A

Аналогичные формулы можно записать для cosβ и cosγ

Теорема косинусов для трехгранного угла

Приведенная форм ул а угла (формула косинусов)

позволяет по трем плоским углам найти

двугранные углы при ребрах трехгранного угла

и, наоборот, зная все двугранные

углы найти все плоские углы при вершине трехгранного угла.

α,β,γ противолежащие им плоские углы

α

β

γ

• Задача №1:
• В трехгранном угле два плоских угла по 45 0 ,а третий плоский угол 60 0 . Найдите двугранный угол , противолежащий третьему углу

Задача №2: Величины двух плоских углов трехгранного угла равны 60 0 и 45 0 . Найдите величину третьего плоского угла, если противолежащий ему двугранный угол - прямой.

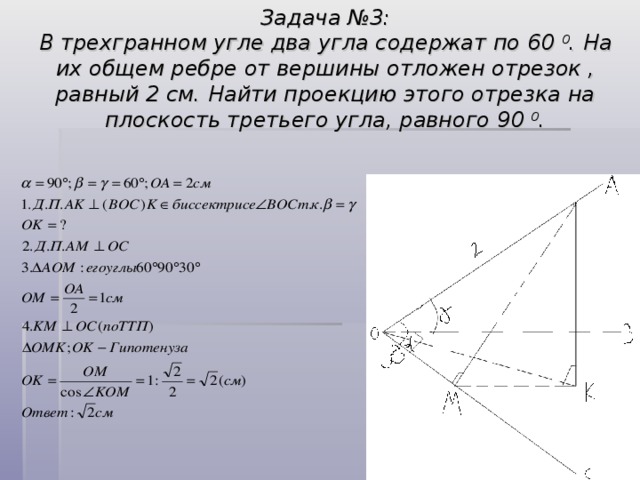
Задача №3: В трехгранном угле два угла содержат по 60 0 . На их общем ребре от вершины отложен отрезок , равный 2 см. Найти проекцию этого отрезка на плоскость третьего угла, равного 90 0 .

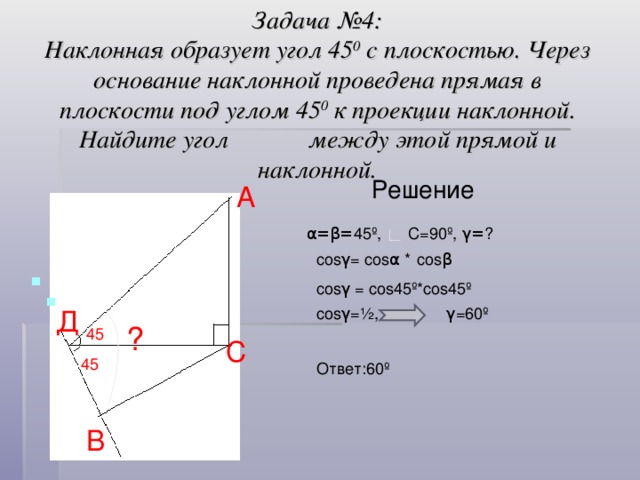
Задача №4: Наклонная образует угол 45 0 с плоскостью. Через основание наклонной проведена прямая в плоскости под углом 45 0 к проекции наклонной. Найдите угол между этой прямой и наклонной.

Решение

А

α=β= 45º, C=90º, γ= ?

cos γ = cos α * cos β

cos γ = cos45º*cos45º

Д

cos γ =½,

γ =60º

?

45

С

45

Ответ :60º

В

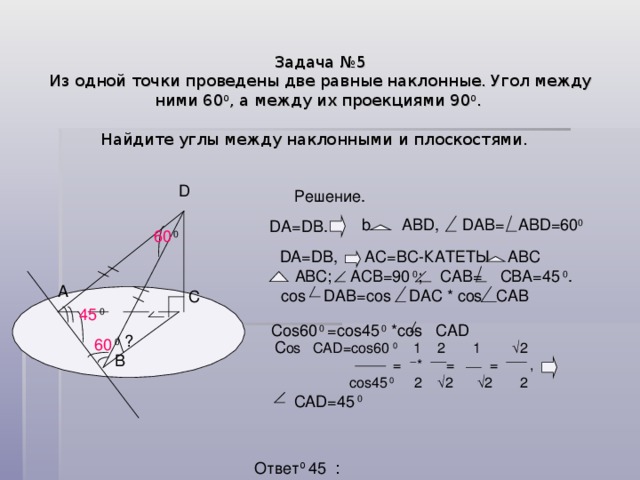
Задача №5 Из одной точки проведены две равные наклонные. Угол между ними 60 0 , а между их проекциями 90 0 . Найдите углы между наклонными и плоскостями.

D

Решение.

ABD,

DAB= ABD=60 0

b

DA=DB.

60 0

DA=DB, AC=BC- КАТЕТЫ ABC

ABC; ACB=90 0 ; CAB= CBA=45 0 .

A

cos DAB=cos DAC * cos CAB

C

45 0

Cos60 0 =cos45 0 *cos CAD

?

60 0

C os CAD= cos60 0 1 2 1 √2

= * = = ,

cos45 0 2 √2 √2 2

B

CAD=45 0

Ответ ׃ 45 0

• Задача№6

В трехгранном угле два плоских угла 45 0 и 30 0 , третий плоский угол 60 0 . Найдите двугранный угол, противолежащий третьему углу. Решение.

• Задача №7

У трехгранного угла два плоских угла равны 45 0 , двугранный угол между ними прямой. Найдите третий плоский угол.

Решение.

Нет тумана, из которого не было бы выхода. Главное – держаться и идти вперёд. Р. Ролан